Difference between revisions of "Aufgaben:Exercise 1.4Z: Entropy of the AMI Code"
m (Text replacement - "generalis" to "generaliz") |
|||
| (28 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Discrete_Sources_with_Memory |
}} | }} | ||
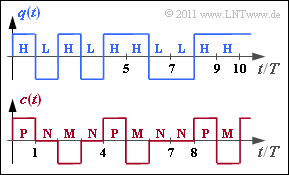
| − | [[File:P_ID2249__Inf_A_1_4.png|right| | + | [[File:P_ID2249__Inf_A_1_4.png|right|frame|Binary source signal (top) and <br>ternary encoder signal (bottom)]] |
| − | + | We assume similar prerequisites as in [[Aufgaben:Exercise_1.4:_Entropy_Approximations_for_the_AMI_Code|Exercise 1.4]] : | |
| − | + | A binary source provides the source symbol sequence $\langle q_\nu \rangle$ with $q_\nu \in \{ {\rm L}, {\rm H} \}$, where there are no statistical bindings between the individual sequence elements. | |
| − | |||
| − | |||
| − | |||
| + | For the symbol probabilities, let: | ||
| + | * $p_{\rm L} =p_{\rm H} = 1/2$ (in subtasks 1 und 2), | ||
| + | * $p_{\rm L} = 1/4, \, p_{\rm H} = 3/4$ (subtasks 3, 4 and 5), | ||
| + | * $p_{\rm L} = 3/4, \, p_{\rm H} = 1/4$ (subtask 6). | ||
| − | |||
| − | + | The presented coded signal $c(t)$ and the corresponding encoded sequence $\langle c_\nu \rangle$ with $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$ results from the AMI coding ("Alternate Mark Inversion") according to the following rule: | |
| − | |||
| + | * The binary symbol $\rm L$ ⇒ "Low" is always represented by the ternary symbol $\rm N$ ⇒ "German: Null" ⇒ "Zero". | ||
| + | * The binary symbol $\rm H$ ⇒ "High" is also encoded deterministically but alternately (hence the name "Alternate Mark Inversion") by the symbols $\rm P$ ⇒ "Plus" and $\rm M$ ⇒ "Minus". | ||
| − | In | + | |
| + | |||
| + | |||
| + | In this task, the decision content $H_0$ and the resulting entropy $H_{\rm C}$ of the encoded sequence $\langle c_\nu \rangle$ are to be determined for the three parameter sets mentioned above. The relative redundancy of the code sequence results from this according to the equation | ||
:$$r_{\rm C} = \frac{H_{\rm 0}-H_{\rm C}}{H_{\rm C}} | :$$r_{\rm C} = \frac{H_{\rm 0}-H_{\rm C}}{H_{\rm C}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This task belongs to the chapter [[Information_Theory/Discrete_Sources_with_Memory|Discrete Sources with Memory]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Discrete_Sources_with_Memory#The_entropy_of_the_AMI_code|The entropy of the AMI code]]. | ||
| + | |||
| + | *In general, the following relations exist between the decision content $H_0$, the entropy $H$ $($here equal to $H_{\rm C})$ and the entropy approximations: | ||
| + | :$$H \le \ \text{...} \ \le H_3 \le H_2 \le H_1 \le H_0 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *In [[Aufgaben:Exercise_1.4:_Entropy_Approximations_for_the_AMI_Code|Exercise 1.4]] the entropy approximations were calculated for equally probable symbols $\rm L$ and $\rm H$ as follows (each in "bit/symbol"): | ||
| + | :$$H_1 = 1.500\hspace{0.05cm},\hspace{0.2cm} H_2 = 1.375\hspace{0.05cm},\hspace{0.2cm}H_3 = 1.292 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Let the source symbols be equally probable $(p_{\rm L} = p_{\rm H}= 1/2)$. What is the entropy $H_{\rm C}$ of the encoded sequence $\langle c_\nu \rangle$? |
|type="{}"} | |type="{}"} | ||
| − | + | $H_{\rm C} \ = \ $ { 1 3% } $\ \rm bit/ternary \ symbol$ | |
| − | { | + | {What is the relative redundancy of the encoded sequence? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $r_{\rm C} \ = \ $ { 36.9 3% } $\ \rm \%$ |
| − | { | + | {For the binary source, $p_{\rm L} = 1/4$ and $p_{\rm H} = 3/4$. What is the entropy of the encoded sequence? |
|type="{}"} | |type="{}"} | ||
| − | + | $H_{\rm C} \ = \ $ { 0.811 3% } $\ \rm bit/ternary \ symbol$ | |
| + | |||
| + | {What is the relative redundancy of the encoded sequence? | ||
| − | |||
|type="{}"} | |type="{}"} | ||
| − | + | $r_{\rm C} \ = \ $ { 48.8 3% } $\ \rm \%$ | |
| − | { | + | {Calculate the approximation $H_{\rm 1}$ of the code entropy for $p_{\rm L} = 1/4$ and $p_{\rm H} = 3/4$. |
|type="{}"} | |type="{}"} | ||
| − | + | $H_{\rm 1} \ = \ $ { 1.56 3% } $\ \rm bit/ternary \ symbol$ | |
| − | { | + | {Calculate the approximation $H_{\rm 1}$ of the code entropy for $p_{\rm L} = 3/4$ and $p_{\rm H} = 1/4$. |
|type="{}"} | |type="{}"} | ||
| − | + | $H_{\rm 1} \ = \ $ { 1.06 3% } $\ \rm bit/ternary \ symbol$ | |
| Line 69: | Line 85: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Since the AMI code neither adds new information nor causes information to disappear, the entropy $H_{\rm C}$ of the encoded sequence $\langle c_\nu \rangle$ is equal to the source entropy $H_{\rm Q}$. | |
| − | :$$H_{\rm Q} {= 1 \,{\rm bit/ | + | *Therefore, for equally probable and statistically independent source symbols, the following holds: |
| + | :$$H_{\rm Q} {= 1 \,{\rm bit/binary \ symbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} \hspace{0.15cm} \underline {= 1 \,{\rm bit/ternary \ symbol}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | |||
| + | '''(2)''' The decision content of a ternary source is $H_0 = \log_2 \; (3) = 1.585\; \rm bit/symbol$. | ||
| + | * This gives the following for the relative redundancy | ||
:$$r_{\rm C} =1 -{H_{\rm C}/H_{\rm 0}}=1-1/{\rm log}_2\hspace{0.05cm}(3) | :$$r_{\rm C} =1 -{H_{\rm C}/H_{\rm 0}}=1-1/{\rm log}_2\hspace{0.05cm}(3) | ||
\hspace{0.15cm} \underline {= 36.9 \,\%} | \hspace{0.15cm} \underline {= 36.9 \,\%} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | |||
| + | '''(3)''' $H_{\rm C} = H_{\rm Q}$ is still valid. However, because of the unequal symbol probabilities, $H_{\rm Q}$ is now smaller: | ||
:$$H_{\rm Q} = \frac{1}{4} \cdot {\rm log}_2\hspace{0.05cm} (4) + \frac{3}{4} \cdot | :$$H_{\rm Q} = \frac{1}{4} \cdot {\rm log}_2\hspace{0.05cm} (4) + \frac{3}{4} \cdot | ||
{\rm log}_2\hspace{0.1cm} (4/3) | {\rm log}_2\hspace{0.1cm} (4/3) | ||
| − | {= 0.811 \,{\rm bit/ | + | {= 0.811 \,{\rm bit/binary \ symbol}} \hspace{0.3cm} |
| − | + | \Rightarrow\hspace{0.3cm} H_{\rm C} = H_{\rm Q} \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/ternary \ symbol}} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | + | ||
| + | '''(4)''' By analogy with sub-task '''(2)''' $r_{\rm C} = 1 - 0.811/1.585 | ||
\hspace{0.15cm} \underline {= 48.8 \,\%} | \hspace{0.15cm} \underline {= 48.8 \,\%} | ||
| + | \hspace{0.05cm}$ now holds. | ||
| + | *One can generalize this result. Namely, it holds: | ||
| + | :$$(1-0.488) = (1- 0.189) \cdot (1- 0.369)\hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm} (1-r_{\rm Codefolge}) = (1-r_{\rm Quelle}) \cdot (1- r_{\rm AMI-Code}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | :$$ | + | |
| − | + | ||
| + | '''(5)''' Since each $\rm L$ is mapped to $\rm N$ and $\rm H$ is mapped alternately to $\rm M$ and $\rm P$, it holds that | ||
| + | :$$p_{\rm N} = p_{\rm L} = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 3/8\hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm} H_1 = {1}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + | ||
| + | 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8/3) \hspace{0.15cm} \underline {= 1.56 \,{\rm bit/ternary \ symbol}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(6)''' Now the probabilities of occurrence of the ternary symbols are $p_{\rm N} = 3/4$ sowie $p_{\rm P} = p_{\rm M} =1/8$. Thus: | |
:$$H_1 = {3}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) + | :$$H_1 = {3}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) + | ||
| − | 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 1.06 \,{\rm bit/ | + | 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 1.06 \,{\rm bit/ternary \ symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | : | + | |
| − | :$$H_0 = 1.585 \,{\rm bit/ | + | ''Interpretation:'' |
| − | \lim_{k \rightarrow \infty } H_k = 0.811 \,{\rm bit/ | + | *For $p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$ gives $H_1 = 1.56 \; \rm bit/symbol$. |
| + | *For $p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$ , on the other hand, $H_1 = 1.06 \; \rm bit/symbol$ results in a significantly smaller value. | ||
| + | *For both parameter combinations, however, the same applies: | ||
| + | :$$H_0 = 1.585 \,{\rm bit/symbol}\hspace{0.05cm},\hspace{0.2cm}H_{\rm C} = | ||
| + | \lim_{k \rightarrow \infty } H_k = 0.811 \,{\rm bit/symbol} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | : | + | It follows from this: <br> |
| − | + | *If one considers two message sources $\rm Q1$ and $\rm Q2$ with the same symbol set size $M$ ⇒ decision content $H_0 = \rm const.$, whereby the first order entropy approximation $(H_1)$ is clearly greater for source $\rm Q1$ than for source $\rm Q2$, one cannot conclude from this by any means that the entropy of $\rm Q1$ is actually greater than the entropy of $\rm Q2$. | |
| − | :* | + | *Rather, one must |
| − | + | :* calculate enough entropy approximations $H_1$, $H_2$, $H_3$, ... for both sources and | |
| − | :* | + | :* determine from them (graphically or analytically) the limit value of $H_k$ for $k \to \infty$. |
| − | + | *Only then a final statement about the entropy ratios is possible. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.2 Sources with Memory^]] |
Latest revision as of 12:48, 22 September 2021
We assume similar prerequisites as in Exercise 1.4 :
A binary source provides the source symbol sequence $\langle q_\nu \rangle$ with $q_\nu \in \{ {\rm L}, {\rm H} \}$, where there are no statistical bindings between the individual sequence elements.
For the symbol probabilities, let:
- $p_{\rm L} =p_{\rm H} = 1/2$ (in subtasks 1 und 2),
- $p_{\rm L} = 1/4, \, p_{\rm H} = 3/4$ (subtasks 3, 4 and 5),
- $p_{\rm L} = 3/4, \, p_{\rm H} = 1/4$ (subtask 6).
The presented coded signal $c(t)$ and the corresponding encoded sequence $\langle c_\nu \rangle$ with $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$ results from the AMI coding ("Alternate Mark Inversion") according to the following rule:
- The binary symbol $\rm L$ ⇒ "Low" is always represented by the ternary symbol $\rm N$ ⇒ "German: Null" ⇒ "Zero".
- The binary symbol $\rm H$ ⇒ "High" is also encoded deterministically but alternately (hence the name "Alternate Mark Inversion") by the symbols $\rm P$ ⇒ "Plus" and $\rm M$ ⇒ "Minus".
In this task, the decision content $H_0$ and the resulting entropy $H_{\rm C}$ of the encoded sequence $\langle c_\nu \rangle$ are to be determined for the three parameter sets mentioned above. The relative redundancy of the code sequence results from this according to the equation
- $$r_{\rm C} = \frac{H_{\rm 0}-H_{\rm C}}{H_{\rm C}} \hspace{0.05cm}.$$
Hints:
- This task belongs to the chapter Discrete Sources with Memory.
- Reference is made in particular to the page The entropy of the AMI code.
- In general, the following relations exist between the decision content $H_0$, the entropy $H$ $($here equal to $H_{\rm C})$ and the entropy approximations:
- $$H \le \ \text{...} \ \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
- In Exercise 1.4 the entropy approximations were calculated for equally probable symbols $\rm L$ and $\rm H$ as follows (each in "bit/symbol"):
- $$H_1 = 1.500\hspace{0.05cm},\hspace{0.2cm} H_2 = 1.375\hspace{0.05cm},\hspace{0.2cm}H_3 = 1.292 \hspace{0.05cm}.$$
Questions
Solution
- Therefore, for equally probable and statistically independent source symbols, the following holds:
- $$H_{\rm Q} {= 1 \,{\rm bit/binary \ symbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} \hspace{0.15cm} \underline {= 1 \,{\rm bit/ternary \ symbol}} \hspace{0.05cm}.$$
(2) The decision content of a ternary source is $H_0 = \log_2 \; (3) = 1.585\; \rm bit/symbol$.
- This gives the following for the relative redundancy
- $$r_{\rm C} =1 -{H_{\rm C}/H_{\rm 0}}=1-1/{\rm log}_2\hspace{0.05cm}(3) \hspace{0.15cm} \underline {= 36.9 \,\%} \hspace{0.05cm}.$$
(3) $H_{\rm C} = H_{\rm Q}$ is still valid. However, because of the unequal symbol probabilities, $H_{\rm Q}$ is now smaller:
- $$H_{\rm Q} = \frac{1}{4} \cdot {\rm log}_2\hspace{0.05cm} (4) + \frac{3}{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) {= 0.811 \,{\rm bit/binary \ symbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} = H_{\rm Q} \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/ternary \ symbol}} \hspace{0.05cm}.$$
(4) By analogy with sub-task (2) $r_{\rm C} = 1 - 0.811/1.585 \hspace{0.15cm} \underline {= 48.8 \,\%} \hspace{0.05cm}$ now holds.
- One can generalize this result. Namely, it holds:
- $$(1-0.488) = (1- 0.189) \cdot (1- 0.369)\hspace{0.3cm} \Rightarrow\hspace{0.3cm} (1-r_{\rm Codefolge}) = (1-r_{\rm Quelle}) \cdot (1- r_{\rm AMI-Code}) \hspace{0.05cm}.$$
(5) Since each $\rm L$ is mapped to $\rm N$ and $\rm H$ is mapped alternately to $\rm M$ and $\rm P$, it holds that
- $$p_{\rm N} = p_{\rm L} = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 3/8\hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_1 = {1}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8/3) \hspace{0.15cm} \underline {= 1.56 \,{\rm bit/ternary \ symbol}} \hspace{0.05cm}.$$
(6) Now the probabilities of occurrence of the ternary symbols are $p_{\rm N} = 3/4$ sowie $p_{\rm P} = p_{\rm M} =1/8$. Thus:
- $$H_1 = {3}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 1.06 \,{\rm bit/ternary \ symbol}} \hspace{0.05cm}.$$
Interpretation:
- For $p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$ gives $H_1 = 1.56 \; \rm bit/symbol$.
- For $p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$ , on the other hand, $H_1 = 1.06 \; \rm bit/symbol$ results in a significantly smaller value.
- For both parameter combinations, however, the same applies:
- $$H_0 = 1.585 \,{\rm bit/symbol}\hspace{0.05cm},\hspace{0.2cm}H_{\rm C} = \lim_{k \rightarrow \infty } H_k = 0.811 \,{\rm bit/symbol} \hspace{0.05cm}.$$
It follows from this:
- If one considers two message sources $\rm Q1$ and $\rm Q2$ with the same symbol set size $M$ ⇒ decision content $H_0 = \rm const.$, whereby the first order entropy approximation $(H_1)$ is clearly greater for source $\rm Q1$ than for source $\rm Q2$, one cannot conclude from this by any means that the entropy of $\rm Q1$ is actually greater than the entropy of $\rm Q2$.
- Rather, one must
- calculate enough entropy approximations $H_1$, $H_2$, $H_3$, ... for both sources and
- determine from them (graphically or analytically) the limit value of $H_k$ for $k \to \infty$.
- Only then a final statement about the entropy ratios is possible.