Difference between revisions of "Aufgaben:Exercise 2.10: SSB-AM with Channel Distortions"
m (Guenter verschob die Seite 2.10 ESB-Modulation mit Kanalverzerrungen nach 2.10 ESB-AM mit Kanalverzerrungen) |
m |
||
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Single-Sideband_Modulation |
}} | }} | ||
| − | [[File:P_ID1045__Mod_A_2_9.png|right|]] | + | [[File:P_ID1045__Mod_A_2_9.png|right|frame|Transmission spectrum of the analytical signal and channel frequency response]] |
| − | + | Let us consider the transmission of the source signal | |
| − | $$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$ | + | :$$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$ |
| − | + | over a Gaussian bandpass channel with center frequency $f_{\rm M} = 48 \ \rm kHz$. | |
| + | *This is different from the carrier frequency $f_{\rm T} = 50 \ \rm kHz$ used in modulation. | ||
| + | *The frequencies $f_2$ and $f_4$ stand for $f = 2 \ \rm kHz$ und $f = 4 \ \rm kHz$, resp. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We will now investigate the following modulation methods with respect to the spectrum $S_+(f)$ of the analytical signal as shown in the upper graph: | |
| − | $ | + | * DSB–AM $($all four spectral lines at $46 \ \rm kHz$, $48 \ \rm kHz$, $52 \ \rm kHz$ and $54 \ \rm kHz)$ ⇒ "double-sideband" , |
| − | + | *USB–AM $($only blue spectral lines at $52 \ \rm kHz$ and $54 \ \rm kHz)$ ⇒ "upper-sideband", | |
| + | *LSB–AM $($only green spectral lines at $46 \ \rm kHz$ and $48 \ \rm kHz)$ ⇒ "lower-sideband". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | In each case, a synchronous demodulator is used to first convert the receiver-side carrier signal | ||
| + | :$$ z_{\rm E} (t) = \left\{ \begin{array}{c} 2 \cdot z(t) \\ 4 \cdot z(t) \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\rm DSB} \hspace{0.05cm}, \\ {\rm USB, LSB} \hspace{0.05cm} \\ \end{array}$$ | ||
| + | by multiplication and then completely suppresses the components at twice the carrier frequency. With an ideal channel $H_{\rm K}(f) = 1$ , $v(t) = q(t)$ would hold in all cases. | ||
| − | === | + | The Gaussian channel considered here is given by the following auxiliary values: |
| + | :$$ H_{\rm K}(f = 46\ {\rm kHz}) = 0.968,\hspace{0.3cm}H_{\rm K}(f = 48\ {\rm kHz}) = 1.000,\hspace{0.3cm} | ||
| + | H_{\rm K}(f = 52\ {\rm kHz}) = 0.882,\hspace{0.3cm}H_{\rm K}(f = 54\ {\rm kHz}) = 0.754\hspace{0.05cm}.$$ | ||
| + | In each case, write the sink signal in the form | ||
| + | :$$v(t) = A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2)) + A_4 \cdot \cos(2 \pi f_4 \cdot (t - \tau_4))\hspace{0.05cm}.$$ | ||
| + | All calculations are to be carried out for both a perfect phase synchronization $(Δϕ_{\rm T} = 0)$ as well as for a phase offset of $Δϕ_{\rm T} = 30^\circ$. This is present, for example, if the transmit-side carrier signal is cosine-shaped and the receiver-side carrier is: | ||
| + | :$$ z_{\rm E} (t) = A_{\rm E} \cdot \cos(\omega_{\rm T} \cdot t - 30^\circ) . $$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Modulation_Methods/Single-Sideband_Modulation|Single-Sideband Modulation]]. | ||
| + | *Reference will also be made to the chapter [[Modulation_Methods/Synchronous_Demodulation|Synchronous Demodulation]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the amplitudes for <u>double-sideband AM</u> and <u>perfect synchronization</u> $(Δϕ_{\rm T} = 0)$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_2 \ = \ $ { 1.882 3% } $\ \rm V$ |
| − | $ | + | $A_4 \ = \ $ { 1.722 3% } $\ \rm V$ |
| − | { | + | {What are the values for $A_2$ and $τ_2$ for <u>double-sideband AM</u> and a <u>phase offset</u> $(Δϕ_{\rm T} = 30^\circ)$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_2 \ = \ $ { 1.63 3% } $\ \rm V$ |
| − | $ | + | $τ_2 \hspace{0.25cm} = \ $ { 0. } $\ \rm µ s$ |
| − | { | + | {Calculate the amplitudes $A_2$ and $A_4$ for <u>upper-sideband AM</u> and <u>perfect synchronization</u> $(Δϕ_{\rm T} = 0)$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_2 \ = \ $ { 1.764 3% } $\ \rm V$ |
| − | $ | + | $A_4 \ = \ $ { 1.508 3% } $\ \rm V$ |
| − | { | + | {Give the signal amplitudes for <u>lower-sideband AM</u> and <u>perfect synchronization</u> $(Δϕ_{\rm T} = 0)$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_2 \ = \ $ { 2 3% } $\ \rm V$ |
| − | $ | + | $A_4 \ = \ $ { 1.936 3% } $\ \rm V$ |
| − | { | + | {In contrast, what are the signal parameters for <u>lower-sideband AM</u> and a <u>phase offset</u> $(Δϕ_{\rm T} = 30^\circ)$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_2 \ = \ $ { 2 3% } $\ \rm V$ |
| − | $ | + | $τ_2 \hspace{0.25cm} = \ $ { 41.6 3% } $\ \rm µ s$ |
| − | $ | + | $A_4 \ = \ $ { 1.936 3% } $\ \rm V$ |
| − | $ | + | $τ_4 \hspace{0.25cm} = \ $ { 20.8 3% } $\ \rm µ s$ |
| − | { | + | {Which of these statements are true given your results? Here, "channel distortions" should always be understood as a kind of attenuation distortion. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + In "double-sideband AM", each channel distortion leads to attenuation distortions. |
| − | - | + | - In "single-sideband AM", each channel distortion leads to phase distortions. |
| − | - | + | - In "double-sideband AM", a phase offset leads to attenuation distortions. |
| − | + | + | + In "single-sideband AM", a phase offset leads to phase distortions. |
| + | |||
| + | </quiz> | ||
| + | ===Solution=== | ||
| + | {{ML-Kopf}} | ||
| + | '''(1)''' For DSB–AM, the following attenuation factors are to be taken into account: | ||
| + | :$$\alpha_2 = {1}/{2} \cdot \left[ H_{\rm K}(f = 48\,{\rm kHz}) + H_{\rm K}(f = 52\,{\rm kHz})\right] = 0.981,$$ | ||
| + | :$$\alpha_4 = {1}{2} \cdot \left[ H_{\rm K}(f = 46\,{\rm kHz}) + H_{\rm K}(f = 54\,{\rm kHz})\right] = 0.861\hspace{0.05cm}.$$ | ||
| + | *Thus, we get the amplitudes $A_2\hspace{0.15cm}\underline{ = 1.882 \ \rm V}$ and $A_4\hspace{0.15cm}\underline{ = 1.722 \ \rm V}$. | ||
| + | |||
| + | '''(2)''' For DSB-AM, a phase offset between the carrier frequencies at transmitter and receiver, resp., leads to one and the same attenuation for all frequencies: | ||
| + | :$$A_2 = \cos (30^\circ) \cdot 1.882\,{\rm V} \hspace{0.15cm}\underline {= 1.630\,{\rm V}},$$ | ||
| + | :$$A_4 = \cos (30^\circ) \cdot 1.722\,{\rm V} = 1.491\,{\rm V}\hspace{0.05cm}.$$ | ||
| + | *The delay times are $τ_2\hspace{0.15cm}\underline {= 0}$ and $τ_4 = 0$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' For USB–AM, the attenuation factor $α_2$ is only determined by $H_{\rm K}(f = 52\ \rm kHz)$. | ||
| + | *Since the principal USB amplitude loss by a factor of $2$ is compensated for by a larger carrier amplitude, the following holds: | ||
| + | :$$A_2 = 0.882 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.764\,{\rm V}},$$ | ||
| + | :$$A_4 = 0.754 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.508\,{\rm V}} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | + | '''(4)''' Analogous to the solution in subtask '''(3)''', we obtain here: | |
| − | + | :$$ A_2 = H_{\rm K}(f = 48\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 2\,{\rm V}},$$ | |
| − | ''' | + | :$$A_4 = H_{\rm K}(f = 46\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.936\,{\rm V}} \hspace{0.05cm}.$$ |
| − | $$ | ||
| − | $$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(5)''' For LSB–AM, the received signal is: |
| − | $$ | + | :$$r(t) = 1\,{\rm V} \cdot \cos( \omega_{\rm 48} \cdot t) + 0.968\,{\rm V} \cdot \cos( \omega_{\rm 46} \cdot t)\hspace{0.05cm}.$$ |
| − | $$ | + | *By multiplication with the receiver-side carrier signal $z_{\rm E}(t) = 4 \cdot \cos( \omega_{\rm 50} \cdot t - \Delta \phi_{\rm T})$, applying the trigonometric addition theorem gives: |
| + | :$$v(t) = r(t) \cdot z_{\rm E}(t) = \hspace{0.15cm}\underline { 2.000\,{\rm V}} \cdot \cos( \omega_{\rm 2} \cdot t - \Delta \phi_{\rm T})+\hspace{0.15cm}\underline { 1.936\,{\rm V}} \cdot \cos( \omega_{\rm 4} \cdot t - \Delta \phi_{\rm T}) | ||
| + | + {\rm components \hspace{0.15cm}around\hspace{0.15cm}} 2f_{\rm T}\hspace{0.05cm}$$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm} A_2 \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.5cm} A_4 \hspace{0.15cm}\underline {= 1.936\,{\rm V}}.$$ | ||
| + | *Considering the downstream lowpass filter, this can also be written as: | ||
| + | :$$ v(t) = A_2 \cdot \cos( \omega_{\rm 2} \cdot (t - \tau_2))+ A_4 \cdot \cos( \omega_{\rm 4} \cdot (t - \tau_4))\hspace{0.05cm}.$$ | ||
| + | *The amplitudes are unchanged compared to subtask '''(4)'''. For the delay times when $Δϕ_{\rm T} = π/6$, we get: | ||
| + | :$$ \tau_2 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_2} = \frac {\pi /6}{2 \pi \cdot 2\,{\rm kHz}} \hspace{0.15cm}\underline {\approx 41.6\,{\rm µ s}},\hspace{0.5cm} \tau_4 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_4}= \frac {\tau_2}{2}\hspace{0.15cm}\underline {\approx 20.8\,{\rm µ s}} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(6)''' The <u>first and last answers</u> are correct: | |
| + | *Also for "single-sideband AM" : Attenuation distortions on the channel lead only to attenuation distortions with respect to $v(t)$. | ||
| + | *Phase distortions are only present for a demodulator with a phase offset in the case of "single-sideband AM". | ||
| + | *For "double-sideband AM", such a phase offset would not result in any distortions, but only in frequency-independent attenuation. | ||
| + | *Phase distortions with respect to $v(t)$ can also arise in "DSB–AM" and "SSB–AM", if these already occur on the channel. | ||
| Line 115: | Line 134: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.4 Single Sideband Amplitude Modulation^]] |
Latest revision as of 16:55, 31 March 2022
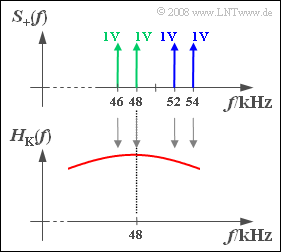
Let us consider the transmission of the source signal
- $$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$
over a Gaussian bandpass channel with center frequency $f_{\rm M} = 48 \ \rm kHz$.
- This is different from the carrier frequency $f_{\rm T} = 50 \ \rm kHz$ used in modulation.
- The frequencies $f_2$ and $f_4$ stand for $f = 2 \ \rm kHz$ und $f = 4 \ \rm kHz$, resp.
We will now investigate the following modulation methods with respect to the spectrum $S_+(f)$ of the analytical signal as shown in the upper graph:
- DSB–AM $($all four spectral lines at $46 \ \rm kHz$, $48 \ \rm kHz$, $52 \ \rm kHz$ and $54 \ \rm kHz)$ ⇒ "double-sideband" ,
- USB–AM $($only blue spectral lines at $52 \ \rm kHz$ and $54 \ \rm kHz)$ ⇒ "upper-sideband",
- LSB–AM $($only green spectral lines at $46 \ \rm kHz$ and $48 \ \rm kHz)$ ⇒ "lower-sideband".
In each case, a synchronous demodulator is used to first convert the receiver-side carrier signal
- $$ z_{\rm E} (t) = \left\{ \begin{array}{c} 2 \cdot z(t) \\ 4 \cdot z(t) \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\rm DSB} \hspace{0.05cm}, \\ {\rm USB, LSB} \hspace{0.05cm} \\ \end{array}$$
by multiplication and then completely suppresses the components at twice the carrier frequency. With an ideal channel $H_{\rm K}(f) = 1$ , $v(t) = q(t)$ would hold in all cases.
The Gaussian channel considered here is given by the following auxiliary values:
- $$ H_{\rm K}(f = 46\ {\rm kHz}) = 0.968,\hspace{0.3cm}H_{\rm K}(f = 48\ {\rm kHz}) = 1.000,\hspace{0.3cm} H_{\rm K}(f = 52\ {\rm kHz}) = 0.882,\hspace{0.3cm}H_{\rm K}(f = 54\ {\rm kHz}) = 0.754\hspace{0.05cm}.$$
In each case, write the sink signal in the form
- $$v(t) = A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2)) + A_4 \cdot \cos(2 \pi f_4 \cdot (t - \tau_4))\hspace{0.05cm}.$$
All calculations are to be carried out for both a perfect phase synchronization $(Δϕ_{\rm T} = 0)$ as well as for a phase offset of $Δϕ_{\rm T} = 30^\circ$. This is present, for example, if the transmit-side carrier signal is cosine-shaped and the receiver-side carrier is:
- $$ z_{\rm E} (t) = A_{\rm E} \cdot \cos(\omega_{\rm T} \cdot t - 30^\circ) . $$
Hints:
- This exercise belongs to the chapter Single-Sideband Modulation.
- Reference will also be made to the chapter Synchronous Demodulation.
Questions
Solution
- $$\alpha_2 = {1}/{2} \cdot \left[ H_{\rm K}(f = 48\,{\rm kHz}) + H_{\rm K}(f = 52\,{\rm kHz})\right] = 0.981,$$
- $$\alpha_4 = {1}{2} \cdot \left[ H_{\rm K}(f = 46\,{\rm kHz}) + H_{\rm K}(f = 54\,{\rm kHz})\right] = 0.861\hspace{0.05cm}.$$
- Thus, we get the amplitudes $A_2\hspace{0.15cm}\underline{ = 1.882 \ \rm V}$ and $A_4\hspace{0.15cm}\underline{ = 1.722 \ \rm V}$.
(2) For DSB-AM, a phase offset between the carrier frequencies at transmitter and receiver, resp., leads to one and the same attenuation for all frequencies:
- $$A_2 = \cos (30^\circ) \cdot 1.882\,{\rm V} \hspace{0.15cm}\underline {= 1.630\,{\rm V}},$$
- $$A_4 = \cos (30^\circ) \cdot 1.722\,{\rm V} = 1.491\,{\rm V}\hspace{0.05cm}.$$
- The delay times are $τ_2\hspace{0.15cm}\underline {= 0}$ and $τ_4 = 0$.
(3) For USB–AM, the attenuation factor $α_2$ is only determined by $H_{\rm K}(f = 52\ \rm kHz)$.
- Since the principal USB amplitude loss by a factor of $2$ is compensated for by a larger carrier amplitude, the following holds:
- $$A_2 = 0.882 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.764\,{\rm V}},$$
- $$A_4 = 0.754 \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.508\,{\rm V}} \hspace{0.05cm}.$$
(4) Analogous to the solution in subtask (3), we obtain here:
- $$ A_2 = H_{\rm K}(f = 48\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 2\,{\rm V}},$$
- $$A_4 = H_{\rm K}(f = 46\,{\rm kHz}) \cdot 2\,{\rm V}\hspace{0.15cm}\underline {= 1.936\,{\rm V}} \hspace{0.05cm}.$$
(5) For LSB–AM, the received signal is:
- $$r(t) = 1\,{\rm V} \cdot \cos( \omega_{\rm 48} \cdot t) + 0.968\,{\rm V} \cdot \cos( \omega_{\rm 46} \cdot t)\hspace{0.05cm}.$$
- By multiplication with the receiver-side carrier signal $z_{\rm E}(t) = 4 \cdot \cos( \omega_{\rm 50} \cdot t - \Delta \phi_{\rm T})$, applying the trigonometric addition theorem gives:
- $$v(t) = r(t) \cdot z_{\rm E}(t) = \hspace{0.15cm}\underline { 2.000\,{\rm V}} \cdot \cos( \omega_{\rm 2} \cdot t - \Delta \phi_{\rm T})+\hspace{0.15cm}\underline { 1.936\,{\rm V}} \cdot \cos( \omega_{\rm 4} \cdot t - \Delta \phi_{\rm T}) + {\rm components \hspace{0.15cm}around\hspace{0.15cm}} 2f_{\rm T}\hspace{0.05cm}$$
- $$ \Rightarrow \hspace{0.3cm} A_2 \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.5cm} A_4 \hspace{0.15cm}\underline {= 1.936\,{\rm V}}.$$
- Considering the downstream lowpass filter, this can also be written as:
- $$ v(t) = A_2 \cdot \cos( \omega_{\rm 2} \cdot (t - \tau_2))+ A_4 \cdot \cos( \omega_{\rm 4} \cdot (t - \tau_4))\hspace{0.05cm}.$$
- The amplitudes are unchanged compared to subtask (4). For the delay times when $Δϕ_{\rm T} = π/6$, we get:
- $$ \tau_2 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_2} = \frac {\pi /6}{2 \pi \cdot 2\,{\rm kHz}} \hspace{0.15cm}\underline {\approx 41.6\,{\rm µ s}},\hspace{0.5cm} \tau_4 = \frac {\Delta \phi_{\rm T}}{2 \pi \cdot f_4}= \frac {\tau_2}{2}\hspace{0.15cm}\underline {\approx 20.8\,{\rm µ s}} \hspace{0.05cm}.$$
(6) The first and last answers are correct:
- Also for "single-sideband AM" : Attenuation distortions on the channel lead only to attenuation distortions with respect to $v(t)$.
- Phase distortions are only present for a demodulator with a phase offset in the case of "single-sideband AM".
- For "double-sideband AM", such a phase offset would not result in any distortions, but only in frequency-independent attenuation.
- Phase distortions with respect to $v(t)$ can also arise in "DSB–AM" and "SSB–AM", if these already occur on the channel.