Difference between revisions of "Aufgaben:Exercise 3.5: Eye Opening with Pseudoternary Coding"
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Intersymbol_Interference_for_Multi-Level_Transmission |
}} | }} | ||
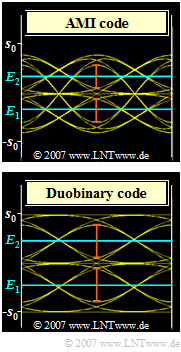
| − | [[File: | + | [[File:EN_Dig_A_3_5.png|right|frame|Eye diagrams with AMI and duobinary code]] |
| − | + | Three digital transmission systems are considered, each with the following matching properties: | |
| − | * NRZ& | + | * NRZ rectangular pulses with amplitude $s_0 = 2 \, {\rm V}$, |
| − | |||
| − | |||
| − | |||
| − | |||
| + | * coaxial cable with characteristic cable attenuation $a_* = 40 \, {\rm dB}$, | ||
| − | + | * AWGN noise with noise power density $N_0$, | |
| − | + | * receiver filter $H_{\rm E}(f) = 1/H_{\rm K}(f) \cdot H_{\rm G}(f) $ consisting of an ideal channel equalizer $H_{\rm K}(f)^{-1}$ and a Gaussian low-pass filter $H_{\rm G}(f)$ with normalized cutoff frequency $f_{\rm G} \cdot T \approx 0.5$, | |
| − | * | + | |
| + | * threshold decision with optimal decision thresholds and optimal detection time $T_{\rm D} = 0$. | ||
| + | |||
| + | |||
| + | The system variants to be investigated in the exercise differ only in terms of the line code: | ||
| + | |||
| + | ⇒ $\text{System A}$ uses a binary bipolar redundancy-free transmission signal. The following descriptive variables are known: | ||
| + | * Basic detection pulse values $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, \text{ ...} \, \approx 0$ | ||
:$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} | :$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} | ||
-g_{1}-g_{-1} = 1.12\,{\rm V} | -g_{1}-g_{-1} = 1.12\,{\rm V} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * Noise rms value $\sigma_d \approx 0.2 \, {\rm V}$ |
| − | :$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ | + | :$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ |
\sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$ | 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | + | ⇒ $\text{System B}$ uses AMI coding: | |
| + | *Here the outer symbols $"+1"$ or $"–1"$ occur only in isolation. | ||
| + | *In the case of three consecutive symbols, the sequences "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, +1, \, +1, \,\text{ ...}$" and "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, 0, \, +1, \, \text{ ...} $" among others, are not possible, | ||
| + | * in contrast to the sequence "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, –1, \, +1, \, \text{ ...} $". | ||
| + | |||
| + | |||
| + | ⇒ $\text{System C}$ uses the duobinary code: | ||
| + | *Here the alternating sequence "$\hspace{-0.1cm} \text{ ...} \, , \, –1, \, +1, \, –1, \, \text{ ...} $" is excluded by the code, which has a favorable effect on the eye opening. | ||
| + | |||
| + | |||
| + | |||
| − | + | Notes: | |
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Intersymbol_Interference_for_Multi-Level_Transmission|"Intersymbol Interference for Multi-Level Transmission"]]. | ||
| + | |||
| + | * Not all of the numerical values given here are necessary to solve this exercise. | ||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the half eye opening for the '''AMI code'''. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System B:}\hspace{0.4cm} \ddot{o}(T_{\rm D})/2 \ = \ $ { 0.45 3% } $\ {\rm V}$ |
| − | { | + | {Calculate the worst-case signal-to-noise ratio for this system. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System B:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ { 7 3% } $\ {\rm dB}$ |
| − | { | + | {How must the thresholds $E_1$ and $E_2$ be chosen so that the result just calculated is correct? |
|type="{}"} | |type="{}"} | ||
| − | $E_1$ | + | $E_1 \ \hspace{0.05cm} = \ ${ -0.69--0.65 } $\ {\rm V}$ |
| − | $E_2$ | + | $E_2 \ = \ $ { 0.667 3% } $\ {\rm V}$ |
| − | { | + | {Calculate the half eye opening at the '''duobinary code'''. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System C:}\hspace{0.4cm} \ddot{o}(T_{\rm D})/2 \ = \ $ { 0.67 3% } $\ {\rm V}$ |
| − | { | + | {Calculate the worst-case signal-to-noise ratio for duobinary coding. |
|type="{}"} | |type="{}"} | ||
| − | ${ | + | $\text{System C:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ { 10.5 3% } $\ {\rm dB}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Since the symbol rate is not changed in the AMI code compared to the redundancy-free binary system, the basic detection pulse values remain unchanged: |
| + | :$$g_0 = 1.56 \, {\rm V}, \ g_1 = g_{\rm –1} = 0.22 \, {\rm V}, \ g_2 = g_{\rm –2} \approx 0.$$ | ||
| + | |||
| + | In pseudo-ternary coding, there are always two eye openings: | ||
| − | + | *The upper boundary line of the upper eye results in the AMI code as in the redundancy-free binary system: | |
| − | :$$d_{\rm | + | :$$d_{\rm top}= g_0 - 2 \cdot g_1 \hspace{0.2cm}\text{(associated sequence: } "\hspace{-0.1cm}-1, +1, -1\hspace{-0.1cm}") |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *In contrast, for the lower boundary line of the upper eye: | |
| − | :$$d_{\rm | + | :$$d_{\rm bottom}= g_1 \hspace{0.2cm}\text{(associated sequences: }\ "\hspace{-0.1cm}0,\ 0, +1\hspace{-0.1cm}"\hspace{0.2cm}\text{ and } "\hspace{-0.1cm}+1,\ 0,\ 0\hspace{-0.1cm}")\hspace{0.05cm}.$$ |
| − | |||
| − | + | Thus, for the half eye opening, the following holds true: | |
| − | :$${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm | + | :$${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm top} - d_{\rm bottom}) = {1}/{2} \cdot g_0 - {3}/{2} \cdot g_1 \hspace{0.15cm}\underline {= |
0.45\,{\rm V}}\hspace{0.05cm}.$$ | 0.45\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | + | The corresponding equation for the redundancy-free binary system is: | |
:$${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$ | :$${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' In terms of noise, there is no difference between the three systems since the same symbol rate is always present. It follows for the AMI code: |
:$$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = | :$$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = | ||
5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 84: | Line 99: | ||
lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$ | lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | + | *The loss compared to the redundancy-free binary system is thus almost $8 \, {\rm dB}$. | |
| + | |||
| + | *The reason for this serious loss of signal-to-noise ratio is that with the AMI code, despite $37\%$ redundancy, the symbol sequence "$\text{ ...} , \, –1, \, +1, \, –1, \text{ ...} $" is not excluded, which is particularly unfavorable with respect to intersymbol interference. | ||
| − | '''(3)''' | + | |
| − | :$$E_2= {1}/{2} \cdot (d_{\rm | + | '''(3)''' The threshold $E_2$ must be in the middle between $d_{\rm top}$ and $d_{\rm bottom}$: |
| + | :$$E_2= {1}/{2} \cdot (d_{\rm top} + d_{\rm bottom}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= | ||
0.67\,{\rm V}}\hspace{0.05cm}.$$ | 0.67\,{\rm V}}\hspace{0.05cm}.$$ | ||
| + | *The threshold value $E_1$ is symmetrical to this: $E_1 \, \underline {= \, –0.67 {\rm V}}$. | ||
| + | |||
| − | |||
| + | '''(4)''' We again assume the same basic detection pulse values. | ||
| + | *The worst-case sequence with respect to the upper boundary line of the upper eye is "$\text{ ...} , 0, \, +1, \, 0, \text{ ...} $", | ||
| + | *while the lower boundary line is defined by "$\text{ ...} , 0, \, 0, \, +1, \text{ ...} $" or "$\text{ ...} , +1, \, 0, \, 0, \text{ ...} $" respectively. | ||
| − | + | *From this follows: | |
| − | :$$d_{\rm | + | :$$d_{\rm top}= g_0, \hspace{0.2cm} d_{\rm bottom} = g_1 \hspace{0.3cm}\Rightarrow |
\hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - | \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - | ||
| − | {g_1}/{2}\hspace{0.15cm}\underline { = 0. | + | {g_1}/{2}\hspace{0.15cm}\underline { = 0.667\,{\rm V}} \hspace{0.05cm}.$$ |
| − | '''(5)''' | + | '''(5)''' Using the result from '''(4)''', we obtain analogous to subtask '''(2)''': |
:$$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = | :$$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = | ||
11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | 11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 107: | Line 129: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Prerequisite for this result are thresholds at | |
:$$E_2= {1}/{2} \cdot (g_0 + g_1 ) = | :$$E_2= {1}/{2} \cdot (g_0 + g_1 ) = | ||
0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$ | 0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$ | ||
| − | + | *It should be noted that the same cutoff frequency $f_{\rm G} \cdot T = 0.5$ was always assumed here. | |
| − | + | ||
| + | *If the cutoff frequency is optimized, it may well be that the duobinary code is superior to the redundancy-free binary code if the characteristic cable attenuation is sufficiently large. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^3.4 Eye Opening with Multilevel Systems^]] |
Latest revision as of 15:45, 28 June 2022
Three digital transmission systems are considered, each with the following matching properties:
- NRZ rectangular pulses with amplitude $s_0 = 2 \, {\rm V}$,
- coaxial cable with characteristic cable attenuation $a_* = 40 \, {\rm dB}$,
- AWGN noise with noise power density $N_0$,
- receiver filter $H_{\rm E}(f) = 1/H_{\rm K}(f) \cdot H_{\rm G}(f) $ consisting of an ideal channel equalizer $H_{\rm K}(f)^{-1}$ and a Gaussian low-pass filter $H_{\rm G}(f)$ with normalized cutoff frequency $f_{\rm G} \cdot T \approx 0.5$,
- threshold decision with optimal decision thresholds and optimal detection time $T_{\rm D} = 0$.
The system variants to be investigated in the exercise differ only in terms of the line code:
⇒ $\text{System A}$ uses a binary bipolar redundancy-free transmission signal. The following descriptive variables are known:
- Basic detection pulse values $g_0 = 1.56 \, {\rm V}$, $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$, $g_2 = g_{\rm –2} = \, \text{ ...} \, \approx 0$
- $$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} -g_{1}-g_{-1} = 1.12\,{\rm V} \hspace{0.05cm}.$$
- Noise rms value $\sigma_d \approx 0.2 \, {\rm V}$
- $$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$
⇒ $\text{System B}$ uses AMI coding:
- Here the outer symbols $"+1"$ or $"–1"$ occur only in isolation.
- In the case of three consecutive symbols, the sequences "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, +1, \, +1, \,\text{ ...}$" and "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, 0, \, +1, \, \text{ ...} $" among others, are not possible,
- in contrast to the sequence "$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, –1, \, +1, \, \text{ ...} $".
⇒ $\text{System C}$ uses the duobinary code:
- Here the alternating sequence "$\hspace{-0.1cm} \text{ ...} \, , \, –1, \, +1, \, –1, \, \text{ ...} $" is excluded by the code, which has a favorable effect on the eye opening.
Notes:
- The exercise belongs to the chapter "Intersymbol Interference for Multi-Level Transmission".
- Not all of the numerical values given here are necessary to solve this exercise.
Questions
Solution
- $$g_0 = 1.56 \, {\rm V}, \ g_1 = g_{\rm –1} = 0.22 \, {\rm V}, \ g_2 = g_{\rm –2} \approx 0.$$
In pseudo-ternary coding, there are always two eye openings:
- The upper boundary line of the upper eye results in the AMI code as in the redundancy-free binary system:
- $$d_{\rm top}= g_0 - 2 \cdot g_1 \hspace{0.2cm}\text{(associated sequence: } "\hspace{-0.1cm}-1, +1, -1\hspace{-0.1cm}") \hspace{0.05cm}.$$
- In contrast, for the lower boundary line of the upper eye:
- $$d_{\rm bottom}= g_1 \hspace{0.2cm}\text{(associated sequences: }\ "\hspace{-0.1cm}0,\ 0, +1\hspace{-0.1cm}"\hspace{0.2cm}\text{ and } "\hspace{-0.1cm}+1,\ 0,\ 0\hspace{-0.1cm}")\hspace{0.05cm}.$$
Thus, for the half eye opening, the following holds true:
- $${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm top} - d_{\rm bottom}) = {1}/{2} \cdot g_0 - {3}/{2} \cdot g_1 \hspace{0.15cm}\underline {= 0.45\,{\rm V}}\hspace{0.05cm}.$$
The corresponding equation for the redundancy-free binary system is:
- $${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$
(2) In terms of noise, there is no difference between the three systems since the same symbol rate is always present. It follows for the AMI code:
- $$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$
- The loss compared to the redundancy-free binary system is thus almost $8 \, {\rm dB}$.
- The reason for this serious loss of signal-to-noise ratio is that with the AMI code, despite $37\%$ redundancy, the symbol sequence "$\text{ ...} , \, –1, \, +1, \, –1, \text{ ...} $" is not excluded, which is particularly unfavorable with respect to intersymbol interference.
(3) The threshold $E_2$ must be in the middle between $d_{\rm top}$ and $d_{\rm bottom}$:
- $$E_2= {1}/{2} \cdot (d_{\rm top} + d_{\rm bottom}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= 0.67\,{\rm V}}\hspace{0.05cm}.$$
- The threshold value $E_1$ is symmetrical to this: $E_1 \, \underline {= \, –0.67 {\rm V}}$.
(4) We again assume the same basic detection pulse values.
- The worst-case sequence with respect to the upper boundary line of the upper eye is "$\text{ ...} , 0, \, +1, \, 0, \text{ ...} $",
- while the lower boundary line is defined by "$\text{ ...} , 0, \, 0, \, +1, \text{ ...} $" or "$\text{ ...} , +1, \, 0, \, 0, \text{ ...} $" respectively.
- From this follows:
- $$d_{\rm top}= g_0, \hspace{0.2cm} d_{\rm bottom} = g_1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - {g_1}/{2}\hspace{0.15cm}\underline { = 0.667\,{\rm V}} \hspace{0.05cm}.$$
(5) Using the result from (4), we obtain analogous to subtask (2):
- $$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = 11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 10.5\,{\rm dB}} \hspace{0.05cm}.$$
- Prerequisite for this result are thresholds at
- $$E_2= {1}/{2} \cdot (g_0 + g_1 ) = 0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$
- It should be noted that the same cutoff frequency $f_{\rm G} \cdot T = 0.5$ was always assumed here.
- If the cutoff frequency is optimized, it may well be that the duobinary code is superior to the redundancy-free binary code if the characteristic cable attenuation is sufficiently large.