Difference between revisions of "Aufgaben:Exercise 4.3: Different Frequencies"
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} |
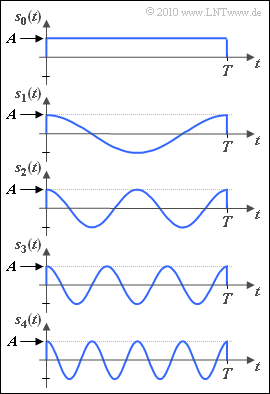
| − | [[File:P_ID1999__Dig_A_4_3.png|right|frame| | + | [[File:P_ID1999__Dig_A_4_3.png|right|frame|Given signal set $\{s_i(t)\}$]] |
| − | In | + | In the diagram $M = 5$ different signals $s_i(t)$ are shown. Contrary to the nomenclature in the theory section, the indexing variable $i$ can have the values $0, \ \text{...} \ , M-1$. |
| − | |||
| − | |||
| − | |||
| − | |||
| + | To be noted: | ||
| + | * All signals are time-limited to $0$ ... $T$; thus the energy of all signals is finite. | ||
| − | + | * The signal $s_1(t)$ has the period $T_0 = T$. The frequency is therefore $f_0 = 1/T$. | |
| − | + | * The signals $s_i(t)$ with $i ≠ 0$ are cosine oscillations with frequency $i \cdot f_0$. | |
| − | * | + | |
| + | *In contrast, $s_0(t)$ is constant between $0$ and $T$. | ||
| + | |||
| + | * The maximum value of all signals is $A$ and $|s_i(t)| ≤ A$ holds. | ||
| + | In this exercise we are looking for the $N$ basis functions, which are numbered here with $j = 0, \ \text{...} \ , N-1$. | ||
| − | === | + | |
| + | |||
| + | Note: The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Question=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Describe the signal set $\{s_i(t)\}$ with $0 ≤ i ≤ 4$ as compactly as possible. <br>Which description form is correct? |
| − | |type=" | + | |type="()"} |
| − | - $s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$. | + | - $s_i(t) = A \cdot \cos {(2\pi \cdot i \cdot t/T)}$. |
| − | + $s_i(t) = A \cdot \cos {(2\pi i \cdot t/T)}$ | + | + $s_i(t) = A \cdot \cos {(2\pi \cdot i \cdot t/T)}$ for $0 ≤ t < T$, otherwise $0$. |
| − | - $s_i(t) = A \cdot \cos {(2\pi t/T \, – \, i \cdot \pi/2)}$ | + | - $s_i(t) = A \cdot \cos {(2\pi t/T \, – \, i \cdot \pi/2)}$ for $0 ≤ t < T$, otherwise $0$. |
| − | { | + | {Specify the number $N$ of basis functions required. |
|type="{}"} | |type="{}"} | ||
| − | $N$ | + | $N \ = \ $ { 5 3% } |
| − | { | + | {What is the basis function $\varphi_0(t)$ that is equal in form to $s_0(t)$? |
| − | |type=" | + | |type="()"} |
- $\varphi_0(t) = s_0(t)$, | - $\varphi_0(t) = s_0(t)$, | ||
| − | + $\varphi_0(t) = | + | + $\varphi_0(t) = \sqrt{1/T}$ for $0 ≤ t < T$, outside $0$. |
| − | - $\varphi_0(t) = | + | - $\varphi_0(t) = \sqrt{2/T}$ for $0 ≤ t < T$, outside $0$. |
| − | { | + | {What is the basis function $\varphi_1(t)$ that is equal in form to $s_1(t)$? |
| − | |type=" | + | |type="()"} |
- $\varphi_1(t) = s_1(t)$, | - $\varphi_1(t) = s_1(t)$, | ||
| − | - $\varphi_1(t) = | + | - $\varphi_1(t) = \sqrt{1/T} \cdot \cos {(2\pi t/T)}$ for $0 ≤ t < T$, outside $0$. |
| − | + $\varphi_1(t) = | + | + $\varphi_1(t) =\sqrt{2/T} \cdot \cos {(2\pi t/T)}$ for $0 ≤ t < T$, outside $0$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>solution 2</u>: |
| + | * This takes into account the different frequencies and the limitation to the range $0 ≤ t < T$. | ||
| + | |||
| + | *The signals $s_i(t)$ according to suggestion 3, on the other hand, do not differ with respect to frequency, but have different phase positions. | ||
| + | |||
| − | '''(2)''' | + | '''(2)''' The energy-limited signals $s_i(t) = A \cdot \cos {(2\pi \cdot i \cdot t/T)}$ are orthogonal to each other ⇒ the inner product of two signals $s_i(t)$, $s_k(t)$ with $i ≠ k$ is always $0$: |
| − | :$$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A^2 \cdot \int_{0}^{T}\cos(2\pi i \cdot t/T) \cdot \cos(2\pi k \cdot t/T)\,{\rm d} t | + | :$$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A^2 \cdot \int_{0}^{T}\cos(2\pi \cdot i \cdot t/T) \cdot \cos(2\pi \cdot k \cdot t/T)\,{\rm d} t $$ |
| − | :$$ \hspace{-0.1cm} \ | + | :$$ \Rightarrow \hspace{0.3cm} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} {A^2}/{2} \cdot \int_{0}^{T}\cos(2\pi (i-k) t/T) \,{\rm d} t + |
\frac{A^2}{2} \cdot \int_{0}^{T}\cos(2\pi (i+k) t/T) \,{\rm d} t | \frac{A^2}{2} \cdot \int_{0}^{T}\cos(2\pi (i+k) t/T) \,{\rm d} t | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *With $i ∈ \{0, \ \text{...} \ , 4\}$ and $k ∈ \{0, \ \text{...}\ , 4\}$ as well as $i ≠ j$, both $i \, - k$ is integer $\ne0$, as is the sum $i + k$. | |
| + | *Thus, both integrals yield the result zero: | ||
:$$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm}= 0 | :$$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm}= 0 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.05cm}\hspace{0.15cm}\underline {N = M = 5} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.05cm}\hspace{0.15cm}\underline {N = M = 5} | ||
| Line 59: | Line 73: | ||
| − | '''(3)''' | + | '''(3)''' The energy of the signal $s_0(t)$, which is constant within $T$, is equal to |
:$$E_0 = ||s_0(t)||^2 = A^2 \cdot T | :$$E_0 = ||s_0(t)||^2 = A^2 \cdot T | ||
| − | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_0(t)|| = A \cdot \sqrt{T} | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_0(t)|| = A \cdot \sqrt{T} \hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} \varphi_0 (t) = \frac{s_0(t)}{||s_0(t)||} = | |
\left\{ \begin{array}{c} 1/\sqrt{T} \\ | \left\{ \begin{array}{c} 1/\sqrt{T} \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | ||
| − | \\ {\rm | + | \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ |
| − | + | Therefore, <u>solution 2</u> is correct. | |
| − | '''(4)''' | + | '''(4)''' The <u>last solution</u> is correct because of |
:$$E_1 = ||s_1(t)||^2 = \frac{A^2 \cdot T}{2} | :$$E_1 = ||s_1(t)||^2 = \frac{A^2 \cdot T}{2} | ||
| − | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_1(t)|| = A \cdot \sqrt{{T}/{2}} | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_1(t)|| = A \cdot \sqrt{{T}/{2}} \hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} \varphi_1 (t) = \frac{s_1(t)}{||s_1(t)||} = | |
\left\{ \begin{array}{c} \sqrt{2/T} \cdot \cos(2\pi t/T) \\ | \left\{ \begin{array}{c} \sqrt{2/T} \cdot \cos(2\pi t/T) \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | ||
| − | \\ {\rm | + | \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.1 Basis Functions & Vector Spaces^]] |
Latest revision as of 15:56, 13 July 2022
In the diagram $M = 5$ different signals $s_i(t)$ are shown. Contrary to the nomenclature in the theory section, the indexing variable $i$ can have the values $0, \ \text{...} \ , M-1$.
To be noted:
- All signals are time-limited to $0$ ... $T$; thus the energy of all signals is finite.
- The signal $s_1(t)$ has the period $T_0 = T$. The frequency is therefore $f_0 = 1/T$.
- The signals $s_i(t)$ with $i ≠ 0$ are cosine oscillations with frequency $i \cdot f_0$.
- In contrast, $s_0(t)$ is constant between $0$ and $T$.
- The maximum value of all signals is $A$ and $|s_i(t)| ≤ A$ holds.
In this exercise we are looking for the $N$ basis functions, which are numbered here with $j = 0, \ \text{...} \ , N-1$.
Note: The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
Question
Solution
- This takes into account the different frequencies and the limitation to the range $0 ≤ t < T$.
- The signals $s_i(t)$ according to suggestion 3, on the other hand, do not differ with respect to frequency, but have different phase positions.
(2) The energy-limited signals $s_i(t) = A \cdot \cos {(2\pi \cdot i \cdot t/T)}$ are orthogonal to each other ⇒ the inner product of two signals $s_i(t)$, $s_k(t)$ with $i ≠ k$ is always $0$:
- $$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A^2 \cdot \int_{0}^{T}\cos(2\pi \cdot i \cdot t/T) \cdot \cos(2\pi \cdot k \cdot t/T)\,{\rm d} t $$
- $$ \Rightarrow \hspace{0.3cm} < \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} {A^2}/{2} \cdot \int_{0}^{T}\cos(2\pi (i-k) t/T) \,{\rm d} t + \frac{A^2}{2} \cdot \int_{0}^{T}\cos(2\pi (i+k) t/T) \,{\rm d} t \hspace{0.05cm}.$$
- With $i ∈ \{0, \ \text{...} \ , 4\}$ and $k ∈ \{0, \ \text{...}\ , 4\}$ as well as $i ≠ j$, both $i \, - k$ is integer $\ne0$, as is the sum $i + k$.
- Thus, both integrals yield the result zero:
- $$< \hspace{-0.1cm}s_i(t), \hspace{0.1cm} s_k(t)\hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.05cm}\hspace{0.15cm}\underline {N = M = 5} \hspace{0.05cm}.$$
(3) The energy of the signal $s_0(t)$, which is constant within $T$, is equal to
- $$E_0 = ||s_0(t)||^2 = A^2 \cdot T \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_0(t)|| = A \cdot \sqrt{T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_0 (t) = \frac{s_0(t)}{||s_0(t)||} = \left\{ \begin{array}{c} 1/\sqrt{T} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
Therefore, solution 2 is correct.
(4) The last solution is correct because of
- $$E_1 = ||s_1(t)||^2 = \frac{A^2 \cdot T}{2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} ||s_1(t)|| = A \cdot \sqrt{{T}/{2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_1 (t) = \frac{s_1(t)}{||s_1(t)||} = \left\{ \begin{array}{c} \sqrt{2/T} \cdot \cos(2\pi t/T) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$