Difference between revisions of "Aufgaben:Exercise 4.2Z: Eight-level Phase Shift Keying"
| (22 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} |
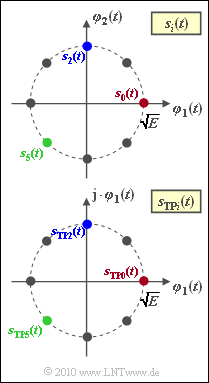
| − | [[File:P_ID1998__Dig_Z_4_2.png|right|frame| | + | [[File:P_ID1998__Dig_Z_4_2.png|right|frame|Signal space points at 8-PSK]] |
| − | + | The $M = 8$ possible transmitted signals at "8–PSK" are with $i = 0, \ \text{...} \ , 7$ in the range $0 ≤ t < T$: | |
:$$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$ | :$$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$ | ||
| − | + | Outside the symbol duration $T$, the signals $s_i(t)$ are all zero. | |
| − | In | + | In [[Aufgaben:Exercise_4.2:_AM/PM_Oscillations|"Exercise 4.2"]] it was shown that this signal set is given by the basis functions |
:$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$ | :$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$ | ||
:$$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$ | :$$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$ | ||
| − | + | which can be represented as follows $(i = 0, \ \text{...} \ , 7)$: | |
:$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | :$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | ||
| − | + | The equivalent low-pass representation of the signals $s_i(t)$ is according to the section [[Modulation_Methods/Quadrature_Amplitude_Modulation#System_description_using_the_equivalent_low-pass_signal|"System description using the equivalent low-pass signal"]] of the book "Modulation methods": | |
:$$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} | :$$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} | ||
| − | \hspace{0.05cm}, \hspace{0.2cm}i = 0, ... \hspace{0.1cm} , 7 \hspace{0.05cm},$$ | + | \hspace{0.05cm}, \hspace{0.2cm}i = 0,\text{...} \hspace{0.1cm} , 7 \hspace{0.05cm},$$ |
| − | + | where $a_i$ are dimensionless complex coefficients and the energy of the basic transmission pulse $g_s(t)$ is $E_{\it g_s}$ in the low-pass region. In the case shown here, $g_s(t)$ describes a rectangular pulse, but any other energy-limited pulse can be used for $g_s(t)$. | |
| − | + | The graph shows the 8–PSK signal space representation | |
| + | #for the band-pass signal $s_{ \it i}(t)$ (top), and | ||
| + | #for the equivalent low-pass signal $s_{\rm TP \it i}(t)$ (bottom): | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | It can be seen from this that the two representations differ only in the basis functions used, with $\varphi_1(t)$ representing different functions in the upper and lower graphs. In the low-pass representation, $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$ holds. | ||
| − | === | + | |
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | ||
| + | |||
| + | * For abbreviation, use the energy $E = 1/2 \cdot A^2 \cdot T$. | ||
| + | |||
| + | * In contrast to the theory section and [[Aufgaben:Exercise_4.2:_AM/PM_Oscillations|"Exercise 4.2"]], here the indexing variable $i$ can take the values $0, \ \text{...} \, ,M-1$. | ||
| + | |||
| + | *The color-coded signal space points in the graph (blue, red, green) are referred to in the questionnaire. These look for the signals $s_0(t)$, $s_2(t)$ and $s_5(t)$. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the coefficients of the signal $s_0(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $s_{\rm 01}$ | + | $s_{\rm 01} \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ |
| − | $s_{\rm 02}$ | + | $s_{\rm 02} \ = \ $ { 0. } $\ \cdot \sqrt{E}$ |
| − | { | + | {What are the coefficients of the signal $s_2(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $s_{\rm 21}$ | + | $s_{\rm 21} \ = \ $ { 0. } $\ \cdot \sqrt{E}$ |
| − | $s_{\rm 22}$ | + | $s_{\rm 22} \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ |
| − | { | + | {What are the coefficients of the signal $s_5(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $s_{\rm 51}$ | + | $s_{\rm 51} \ = \ $ { -0.72821--0.68579 } $\ \cdot \sqrt{E}$ |
| − | $s_{\rm 52}$ | + | $s_{\rm 52} \ = \ $ { -0.72821--0.68579 } $\ \cdot \sqrt{E}$ |
| − | { | + | {By which basis functions can the low–pass signals $s_{\rm TP \it i}(t)$ be represented? By |
|type="[]"} | |type="[]"} | ||
| − | + | + | + one complex basis function $\xi_1(t)$, |
| − | - | + | - two complex basis functions $\xi_1(t)$ and $\xi_2(t)$, |
| − | + | + | + two real functions $\varphi_1(t)$ and $\psi_1(t)$. |
| − | { | + | {What are the real basis functions in the present case? |
|type="[]"} | |type="[]"} | ||
- $\varphi_1(t) = g_s(t)$, | - $\varphi_1(t) = g_s(t)$, | ||
| − | + $\varphi_1(t) = g_s(t)/E_{\rm | + | + $\varphi_1(t) = g_s(t)/\sqrt{E_{\rm g_s}}$, |
+ $\psi_1(t) = \varphi_1(t)$, | + $\psi_1(t) = \varphi_1(t)$, | ||
| − | - $\psi_1(t) = j \cdot \varphi_1(t)$. | + | - $\psi_1(t) = {\rm j} \cdot \varphi_1(t)$. |
| − | { | + | {Let $s_{\rm TP0}(t) = \sqrt{E}$. Which is true? |
|type="()"} | |type="()"} | ||
| − | - | + | - The energy $E$ refers to the low–pass signal. |
| − | + | + | + The energy $E$ refers to the band–pass signal. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The signal $s_0(t)$ is: |
:$$s_0(t)= A \cdot \cos(2\pi f_{\rm T}t ) = s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | :$$s_0(t)= A \cdot \cos(2\pi f_{\rm T}t ) = s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | ||
| − | + | *Since this signal has no sinusoidal part, $s_{\rm 02} \hspace{0.15cm}\underline {= 0}$. | |
| + | *Further, with the given abbreviation: | ||
:$$A = s_{01} \cdot \sqrt{{2}/{T}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$A = s_{01} \cdot \sqrt{{2}/{T}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
s_{01}=\sqrt{1/2 \cdot A^2 \cdot T} = \sqrt{E}\hspace{0.05cm} \hspace{0.15cm}\underline { = 1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$ | s_{01}=\sqrt{1/2 \cdot A^2 \cdot T} = \sqrt{E}\hspace{0.05cm} \hspace{0.15cm}\underline { = 1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The signal $s_2(t)$ is with $i = 2$ (note that the second basis function is minus–sine): |
| − | :$$s_2(t)= A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{2})= - A \cdot \sin(2\pi f_{\rm T}t ) | + | :$$s_2(t)= A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{2})= - A \cdot \sin(2\pi f_{\rm T}t )\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} s_{21}\hspace{0.05cm} \underline{= 0}\hspace{0.05cm}, \hspace{0.2cm} s_{22}= \sqrt{E} \hspace{0.05cm} \hspace{0.15cm}\underline {=1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$ | |
| − | '''(3)''' | + | '''(3)''' According to the solutions to subtasks '''(1)''' and '''(2)''', the following is true: |
:$$s_{51}= s_{52}= - \sqrt{E/2} \hspace{0.05cm} \hspace{0.15cm}\underline { = -0.707 \cdot E^{\hspace{0.05cm}0.5}}$$ | :$$s_{51}= s_{52}= - \sqrt{E/2} \hspace{0.05cm} \hspace{0.15cm}\underline { = -0.707 \cdot E^{\hspace{0.05cm}0.5}}$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm} s_{5}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - {A}/{ \sqrt{2}} \cdot \cos(2\pi f_{\rm T}t ) - {A}/{ \sqrt{2}} \cdot \sin(2\pi f_{\rm T}t )= | + | :$$\Rightarrow \hspace{0.3cm} s_{5}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - {A}/{ \sqrt{2}} \cdot \cos(2\pi f_{\rm T}t ) - {A}/{ \sqrt{2}} \cdot \sin(2\pi f_{\rm T}t )=A \cdot \cos(2\pi f_{\rm T}t + \phi_5)\hspace{0.2cm}{\rm with}\hspace{0.2cm}\phi_5 = -0.75 \cdot \pi |
| − | + | \hspace{0.2cm}{\rm and}\hspace{0.2cm}\phi_5 = 1.25 \cdot \pi | |
| − | \hspace{0.2cm}{\rm | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' <u>Solutions 1 and 3</u> are correct. The following relation holds: |
:$$\xi_1 (t) = \varphi_1 (t) + {\rm j} \cdot \psi_1 (t)\hspace{0.05cm}.$$ | :$$\xi_1 (t) = \varphi_1 (t) + {\rm j} \cdot \psi_1 (t)\hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' Correct are the <u>alternatives 2 and 3</u>: |
| + | *The basis function must be energy-normalized. | ||
| + | |||
| + | * Like $\psi_1(t)$, the basis $\varphi_1(t)$ is a real function, not an imaginary one: | ||
:$$\varphi_1 (t) = \psi_1 (t) = | :$$\varphi_1 (t) = \psi_1 (t) = | ||
\left\{ \begin{array}{c} 1/\sqrt{T} \\ | \left\{ \begin{array}{c} 1/\sqrt{T} \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | ||
| − | \\ {\rm | + | \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ |
| − | '''(6)''' | + | '''(6)''' From the low–pass signal $s_{\rm TP0}(t)$, one can also calculate the band-pass signal $s_0(t)$. |
| − | :$$s_0(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[s_{{\rm TP}0}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ] | + | *In the range $0 ≤ t ≤ T$, the result from '''(5)''' gives the same result as in subtask '''(1)''': |
| − | = {\rm Re}[\sqrt{E} | + | :$$s_0(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\left[s_{{\rm TP}0}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right] |
| − | + | = {\rm Re}\left[\sqrt{E} /{\sqrt{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right]= \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t ) | |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | + | *It follows: The energy $E$ refers to the band–pass signal even when considered in the equivalent low–pass region. | |
| − | + | *Accordingly, for the signal $s_2(t)$ marked with blue dot in the region of interest: | |
| − | :$$s_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ] | + | :$$s_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] |
| − | = | + | = {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t)- \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \big] |
| − | + | = - \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) | |
| − | = | ||
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Finally, for the (green) signal $s_5(t)$ in the range $0 ≤ t < T$ can be written: | |
| − | :$$s_5(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}[\frac{-1 - {\rm j}}{\sqrt{2}} \cdot \sqrt{{E}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} ] = ... | + | :$$s_5(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\frac{-1 - {\rm j}}{\sqrt{2}} \cdot \sqrt{{E}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] = \text{...} |
| − | = | + | = - \sqrt{\frac{E}{2T}} \cdot \cos(2\pi f_{\rm T}t)+ \sqrt{\frac{E}{2T}} \cdot \sin(2\pi f_{\rm T}t)=\sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t + 1.25 \cdot \pi) |
| − | |||
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *These results also agree with those of subtasks '''(2)''' resp. '''(3)'''. Therefore, <u>solution 2</u> is correct. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.1 Basis Functions & Vector Spaces^]] |
Latest revision as of 09:41, 12 August 2022
The $M = 8$ possible transmitted signals at "8–PSK" are with $i = 0, \ \text{...} \ , 7$ in the range $0 ≤ t < T$:
- $$s_i(t)= A \cdot \cos(2\pi f_{\rm T}t + i \cdot {\pi}/{4}) \hspace{0.05cm}.$$
Outside the symbol duration $T$, the signals $s_i(t)$ are all zero.
In "Exercise 4.2" it was shown that this signal set is given by the basis functions
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},$$
- $$\varphi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}$$
which can be represented as follows $(i = 0, \ \text{...} \ , 7)$:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}.$$
The equivalent low-pass representation of the signals $s_i(t)$ is according to the section "System description using the equivalent low-pass signal" of the book "Modulation methods":
- $$s_{{\rm TP}i}(t)= a_{i} \cdot g_s(t) \hspace{0.05cm}, \hspace{0.2cm}a_{i} = a_{{\rm I}i} + {\rm j} \cdot a_{{\rm Q}i} \hspace{0.05cm}, \hspace{0.2cm}i = 0,\text{...} \hspace{0.1cm} , 7 \hspace{0.05cm},$$
where $a_i$ are dimensionless complex coefficients and the energy of the basic transmission pulse $g_s(t)$ is $E_{\it g_s}$ in the low-pass region. In the case shown here, $g_s(t)$ describes a rectangular pulse, but any other energy-limited pulse can be used for $g_s(t)$.
The graph shows the 8–PSK signal space representation
- for the band-pass signal $s_{ \it i}(t)$ (top), and
- for the equivalent low-pass signal $s_{\rm TP \it i}(t)$ (bottom):
It can be seen from this that the two representations differ only in the basis functions used, with $\varphi_1(t)$ representing different functions in the upper and lower graphs. In the low-pass representation, $\varphi_2(t) = {\rm j} \cdot \varphi_1(t)$ holds.
Notes:
- The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
- For abbreviation, use the energy $E = 1/2 \cdot A^2 \cdot T$.
- In contrast to the theory section and "Exercise 4.2", here the indexing variable $i$ can take the values $0, \ \text{...} \, ,M-1$.
- The color-coded signal space points in the graph (blue, red, green) are referred to in the questionnaire. These look for the signals $s_0(t)$, $s_2(t)$ and $s_5(t)$.
Questions
Solution
- $$s_0(t)= A \cdot \cos(2\pi f_{\rm T}t ) = s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm}.$$
- Since this signal has no sinusoidal part, $s_{\rm 02} \hspace{0.15cm}\underline {= 0}$.
- Further, with the given abbreviation:
- $$A = s_{01} \cdot \sqrt{{2}/{T}}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} s_{01}=\sqrt{1/2 \cdot A^2 \cdot T} = \sqrt{E}\hspace{0.05cm} \hspace{0.15cm}\underline { = 1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$
(2) The signal $s_2(t)$ is with $i = 2$ (note that the second basis function is minus–sine):
- $$s_2(t)= A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{2})= - A \cdot \sin(2\pi f_{\rm T}t )\hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{21}\hspace{0.05cm} \underline{= 0}\hspace{0.05cm}, \hspace{0.2cm} s_{22}= \sqrt{E} \hspace{0.05cm} \hspace{0.15cm}\underline {=1 \cdot E^{\hspace{0.05cm}0.5}}\hspace{0.05cm}.$$
(3) According to the solutions to subtasks (1) and (2), the following is true:
- $$s_{51}= s_{52}= - \sqrt{E/2} \hspace{0.05cm} \hspace{0.15cm}\underline { = -0.707 \cdot E^{\hspace{0.05cm}0.5}}$$
- $$\Rightarrow \hspace{0.3cm} s_{5}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - {A}/{ \sqrt{2}} \cdot \cos(2\pi f_{\rm T}t ) - {A}/{ \sqrt{2}} \cdot \sin(2\pi f_{\rm T}t )=A \cdot \cos(2\pi f_{\rm T}t + \phi_5)\hspace{0.2cm}{\rm with}\hspace{0.2cm}\phi_5 = -0.75 \cdot \pi \hspace{0.2cm}{\rm and}\hspace{0.2cm}\phi_5 = 1.25 \cdot \pi \hspace{0.05cm}.$$
(4) Solutions 1 and 3 are correct. The following relation holds:
- $$\xi_1 (t) = \varphi_1 (t) + {\rm j} \cdot \psi_1 (t)\hspace{0.05cm}.$$
(5) Correct are the alternatives 2 and 3:
- The basis function must be energy-normalized.
- Like $\psi_1(t)$, the basis $\varphi_1(t)$ is a real function, not an imaginary one:
- $$\varphi_1 (t) = \psi_1 (t) = \left\{ \begin{array}{c} 1/\sqrt{T} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
(6) From the low–pass signal $s_{\rm TP0}(t)$, one can also calculate the band-pass signal $s_0(t)$.
- In the range $0 ≤ t ≤ T$, the result from (5) gives the same result as in subtask (1):
- $$s_0(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\left[s_{{\rm TP}0}(t) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right] = {\rm Re}\left[\sqrt{E} /{\sqrt{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \right]= \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$
- It follows: The energy $E$ refers to the band–pass signal even when considered in the equivalent low–pass region.
- Accordingly, for the signal $s_2(t)$ marked with blue dot in the region of interest:
- $$s_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] = {\rm Re}\big[\hspace{0.05cm}{\rm j} \cdot \sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t)- \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \big] = - \sqrt{E/T} \cdot \sin(2\pi f_{\rm T}t) \hspace{0.05cm}.$$
- Finally, for the (green) signal $s_5(t)$ in the range $0 ≤ t < T$ can be written:
- $$s_5(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Re}\big[\frac{-1 - {\rm j}}{\sqrt{2}} \cdot \sqrt{{E}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}2\pi f_{\rm T}t} \big] = \text{...} = - \sqrt{\frac{E}{2T}} \cdot \cos(2\pi f_{\rm T}t)+ \sqrt{\frac{E}{2T}} \cdot \sin(2\pi f_{\rm T}t)=\sqrt{E/T} \cdot \cos(2\pi f_{\rm T}t + 1.25 \cdot \pi) \hspace{0.05cm}.$$
- These results also agree with those of subtasks (2) resp. (3). Therefore, solution 2 is correct.