Difference between revisions of "Aufgaben:Exercise 4.14: 8-PSK and 16-PSK"
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation}} |
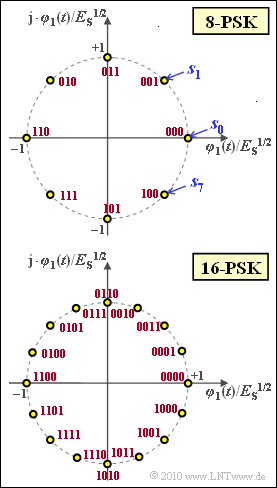
| − | [[File:P_ID2067__Dig_A_4_14.png|right|frame| | + | [[File:P_ID2067__Dig_A_4_14.png|right|frame|Signal space constellations <br>of the 8-PSK and 16-PSK]] |
| − | + | Now a signal set $\{s_i(t)\}$ is considered, which is limited to the time domain $0 ≤ t ≤ T$. The index $i$ runs through the values $0, \ \text{...} \ , M-1$: | |
:$$s_i(t) = A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) \hspace{0.05cm}.$$ | :$$s_i(t) = A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) \hspace{0.05cm}.$$ | ||
| − | + | *This is a "phase modulation" with $M$ signal shapes. | |
| − | + | *This modulation process is also called "$\rm M–PSK$". $M$ is usually a power of two. | |
| − | + | ||
| + | The graphic shows the signal space constellation for $M = 8$ (top) and $M = 16$ (bottom). All signal space points have equal energy $||\boldsymbol{s}_i||^2 = E_{\rm S}$ ("average symbol energy"). | ||
| + | |||
| + | The exact calculation of the symbol error probability is difficult for $M ≠ 2$. However, the so-called "Union Bound" can always be given as an upper bound for the symbol error probability $(p_{\rm UB} ≥ p_{\rm S})$: | ||
:$$ p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) = 2 \cdot {\rm Q} \left (\sqrt{ \frac{ d^2}{ 2 N_0}}\right ) \hspace{0.05cm}.$$ | :$$ p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) = 2 \cdot {\rm Q} \left (\sqrt{ \frac{ d^2}{ 2 N_0}}\right ) \hspace{0.05cm}.$$ | ||
| − | + | The following quantities are used here: | |
| − | * $d$ | + | * $d$ is the distance between two neighboring points, for example between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$. |
| − | * | + | |
| − | * | + | *If the decision boundary is exactly centered perpendicular to the line connecting $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$, then $d/2$ is the distance of $\boldsymbol{s}_0$ or $\boldsymbol{s}_1$ from this decision boundary. |
| − | * ${\rm Q}(x)$ | + | |
| + | * The variance of the AWGN noise is $\sigma_n^2 = N_0/2$. | ||
| + | |||
| + | * The factor of $2$ in the above limit takes into account that for $M > 2$ each signal space point can be falsified in two directions, e.g. for the "8–PSK" the symbol $\boldsymbol{s}_0$ into the symbol $\boldsymbol{s}_1$ or into the symbol $\boldsymbol{s}_7$. | ||
| + | |||
| + | * ${\rm Q}(x)$ is the complementary Gaussian error function for which the following approximation holds: | ||
:$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} | :$${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The last subtask deals with the bit error probability. For this, the following bound was given in the [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation| "theory section"]] under the assumption of a "Gray code": | |
:$$p_{\rm B} \le \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) | :$$p_{\rm B} \le \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | However, this equation is only applicable for $M > 4$. In contrast, the exact solution | |
| − | * | + | * for $M = 2$ from the identity with the [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Binary_phase_shift_keying_.28BPSK.29| "BPSK"]], and |
| − | |||
| − | |||
| − | + | * for $M = 4$ from the fact that the "4–PSK" is identical with the [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Quadrature_amplitude_modulation_.28M-QAM.29|"4–QAM"]]: | |
:$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) | :$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Notes: | ||
| + | * The exercise belongs to the topic of the chapter [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation|"Carrier Frequency Systems with Coherent Demodulation"]]. | ||
| + | *Reference is made in particular to the section [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Multi-level_phase.E2.80.93shift_keying_.28M.E2.80.93PSK.29| "Multi-level Phase Shift Keying"]]. | ||
| + | |||
| + | * The assignment of the $8$ or $16$ symbols to binary sequences of length $3$ or $4$ according to the Gray coding can be taken from the graphic (red labeling). | ||
| + | * When solving the exercise, you can use the following equations: | ||
| + | :$$\cos(\alpha + \beta) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(\alpha ) \cdot \cos( \beta) - \sin(\alpha ) \cdot \sin( \beta)\hspace{0.05cm}, \hspace{0.25cm} | ||
| + | 1 - \cos(2\alpha ) = \sin^2(\alpha )\hspace{0.05cm},$$ | ||
| + | :$$ \int_{0}^{T} \cos^2 ( 2\pi f_{\rm T}t) \,{\rm d} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{0.15cm}{\rm falls}\hspace{0.15cm} f_{\rm T} \gg 1/T \hspace{0.05cm}.$$ | ||
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the basis functions in the band-pass representation? Let $\varphi_1(t)$ and $\varphi_2(t)$ each be limited to the range $0 ≤ t ≤ T$. |
|type="[]"} | |type="[]"} | ||
- $\varphi_1(t) = \cos {(2\pi f_{\rm T}t)}$, | - $\varphi_1(t) = \cos {(2\pi f_{\rm T}t)}$, | ||
| − | + $\varphi_1(t) = | + | + $\varphi_1(t) = \sqrt {2/T} \cdot \cos {(2\pi f_{\rm T}t)}$, |
- $\varphi_2(t) = E_{\rm S} \cdot \sin {(2\pi f_{\rm T}t)}$, | - $\varphi_2(t) = E_{\rm S} \cdot \sin {(2\pi f_{\rm T}t)}$, | ||
| − | + $\varphi_2(t) = \, – | + | + $\varphi_2(t) = \, –\sqrt {2/T} \cdot \sin {(2\pi f_{\rm T}t)}$. |
| − | { | + | {What are the in-phase and quadrature components of the signal space point $\boldsymbol{s}_i$? Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + $s_{\rm I \it i} = E_{\rm S} | + | + $s_{\rm I \it i} = \sqrt {E_{\rm S}} \cdot \cos {(2\pi \cdot i/M)}$, |
| − | - $s_{\rm I \it i} = E_{\rm S} | + | - $s_{\rm I \it i} = \sqrt {E_{\rm S}} \cdot \sin {(2\pi \cdot i/M)}$, |
| − | - $s_{\rm Q \it i} = E_{\rm S} | + | - $s_{\rm Q \it i} = \sqrt {E_{\rm S}} \cdot \cos {(2\pi \cdot i/M)}$, |
| − | + $s_{\rm Q \it i} = E_{\rm S} | + | + $s_{\rm Q \it i} = \sqrt {E_{\rm S}} \cdot \sin {(2\pi \cdot i/M)}$. |
| − | { | + | {What is the distance $d$ between two adjacent signal space points? What are the values for $M = 8$ and $M = 16$, respectively? |
|type="{}"} | |type="{}"} | ||
| − | $M = 8 \text{:} \hspace{0. | + | $M = 8 \text{:} \hspace{0.45cm} d \ = \ $ { 0.765 3% } $\ \cdot \sqrt {E_{\rm S}}$ |
| − | $M = 16 \text{:} \hspace{0.2cm} d$ | + | $M = 16 \text{:} \hspace{0.2cm} d \ = \ $ { 0.39 3% } $\ \cdot \sqrt {E_{\rm S}}$ |
| − | { | + | {What is the value of the "Union Bound" $(p_{\rm UB})$ with $E_{\rm S}/N_0 = 50$. |
|type="{}"} | |type="{}"} | ||
| − | $M = 8 \text{:} \hspace{0. | + | $M = 8 \text{:} \hspace{0.45cm} p_{\rm UB}$ = { 0.014 3% } $\ \%$ |
| − | $M = 16 \text{:} \hspace{0.2cm} p_{\rm UB}$ = { 6 3% } $\ \ | + | $M = 16 \text{:} \hspace{0.2cm} p_{\rm UB}$ = { 6 3% } $\ \%$ |
| − | { | + | {Does the statement "$p_{\rm UB}$ approximates $p_{\rm S}$ more closely the larger $M$ is" hold? |
|type="()"} | |type="()"} | ||
| − | + | + | + YES. |
| − | - | + | - NO. |
| − | { | + | {Which statements are true regarding the bit error probability $p_{\rm B}$? |
|type="[]"} | |type="[]"} | ||
| − | + $p_{\rm B}$ | + | + $p_{\rm B}$ is smallest for $M = 2$ and $M = 4$. |
| − | - $p_{\rm B}$ | + | - $p_{\rm B}$ is smallest for $M = 8$. |
| − | - $p_{\rm B}$ | + | - $p_{\rm B}$ is smallest for $M = 16$. |
| − | + $p_{\rm B}$ | + | + $p_{\rm B}$ is not the main reason for using higher level PSK. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solutions 2 and 4</u> are correct: |
| − | :$$s_i(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) = | + | *The signal set $\{s_i(t)\}$ can be represented in the band-pass domain with the given trigonometric transformation as follows: |
| − | + | :$$s_i(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) = A \cdot \cos \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \cos \left ( 2\pi f_{\rm T}t \right )- | |
A \cdot \sin \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \sin \left ( 2\pi f_{\rm T}t \right )\hspace{0.05cm}.$$ | A \cdot \sin \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \sin \left ( 2\pi f_{\rm T}t \right )\hspace{0.05cm}.$$ | ||
| − | + | *The respective first terms in this difference lead to the signal space point $\boldsymbol{s}_i$, the respective second terms to the basis functions $\varphi_1(t)$ and $\varphi_2(t)$. | |
| − | :$$\int_{0}^{T} \varphi_1 ( t)^2 \,{\rm d} t = \int_{0}^{T} \left [K \cdot \cos( 2\pi f_{\rm T}t)\right ]^2 \,{\rm d} t = 1 | + | |
| − | + | *Here it is to be noted that these must be energy normalized in each case: | |
| + | :$$\int_{0}^{T} \varphi_1 ( t)^2 \,{\rm d} t = \int_{0}^{T} \left [K \cdot \cos( 2\pi f_{\rm T}t)\right ]^2 \,{\rm d} t = 1\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} \frac{K^2 \cdot T}{2} = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = \sqrt{2/T } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
\varphi_1 ( t) = \sqrt{2/T } \cdot \cos( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$ | \varphi_1 ( t) = \sqrt{2/T } \cdot \cos( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$ | ||
| − | + | *Using the same arithmetic, we arrive at the second basis function: | |
| − | |||
:$$\varphi_2 ( t) = -\sqrt{2/T } \cdot \sin( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$ | :$$\varphi_2 ( t) = -\sqrt{2/T } \cdot \sin( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | '''(2)''' <u>Solutions 1 and 4</u> are correct: | |
| − | '''(2)''' | + | *Using the basis functions just calculated, the signal set $s_i(t)$ can be represented as follows $($again, limited to the range $0 ≤ t ≤ T)$: |
:$$s_i(t) = A \cdot \sqrt{T/2 } \cdot \cos ( 2\pi \cdot i /M ) \cdot \varphi_1 ( t)+ | :$$s_i(t) = A \cdot \sqrt{T/2 } \cdot \cos ( 2\pi \cdot i /M ) \cdot \varphi_1 ( t)+ | ||
A \cdot \sqrt{T/2 } \cdot \sin ( 2\pi \cdot i /M ) \cdot \varphi_2 ( t) | A \cdot \sqrt{T/2 } \cdot \sin ( 2\pi \cdot i /M ) \cdot \varphi_2 ( t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *With the energy $E = 0.5 \cdot A^2 \cdot T$, which is the same for all $M$ points and which is also the average signal energy per symbol $(E_{\rm S})$, the above equation is | |
:$$s_i(t) = s_{{\rm I}i} \cdot \varphi_1 ( t)+ | :$$s_i(t) = s_{{\rm I}i} \cdot \varphi_1 ( t)+ | ||
| − | s_{{\rm Q}i} \cdot \varphi_2 ( t) | + | s_{{\rm Q}i} \cdot \varphi_2 ( t)\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm} s_{{\rm I}i} = \sqrt{E_{\rm S} }\cdot \cos ( 2\pi \cdot i /M )\hspace{0.05cm},\hspace{0.2cm} | |
s_{{\rm Q}i} = \sqrt{E_{\rm S} }\cdot \sin ( 2\pi \cdot i /M )\hspace{0.05cm}. $$ | s_{{\rm Q}i} = \sqrt{E_{\rm S} }\cdot \sin ( 2\pi \cdot i /M )\hspace{0.05cm}. $$ | ||
| − | + | *The signal space points sketched in the front graph for $M = 8$ resp. $M = 16$, can be represented in exactly this way. | |
| + | |||
| + | |||
| + | '''(3)''' Since the distance from one to the nearest point is the same for all $i$, we can calculate $d$, for example, from the signal space points $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$. | ||
| + | *In doing so, consider the sketch below. According to the "Pythagorean theorem": | ||
| + | [[File:P_ID2070__Dig_A_4_14c.png|right|frame|Distance calculation at the "8-PSK"]] | ||
| − | + | :$$d_{\rm norm}^2 \hspace{-0.01cm}=\hspace{-0.01cm} \sin^2(\frac{2\pi}{M}) + [1- \cos(\frac{2\pi}{M})]^2 $$ | |
| − | :$$d_{\rm norm}^2 \hspace{-0.01cm}=\hspace{-0.01cm} \sin^2(\frac{2\pi}{M}) + [1- \cos(\frac{2\pi}{M})]^2 | + | :$$\Rightarrow \hspace{0.3cm} d_{\rm norm}^2 \hspace{-0.01cm}=\hspace{-0.01cm} 2 \cdot [1- \cos( \frac{2\pi}{M} )] = 4 \cdot \sin^2(\pi/M )\hspace{0.05cm} $$ |
| − | :$$\hspace{-0.01cm}=\hspace{-0.01cm} 2 \cdot [1- \cos( \frac{2\pi}{M} )] = 4 \cdot \sin^2(\pi/M )\hspace{0.05cm} $$ | + | :$$\Rightarrow \hspace{0.3cm} d_{\rm norm}= 2 \cdot \sin({\pi}/{M }) \hspace{0.3cm} |
| − | :$$\Rightarrow \hspace{0. | + | \Rightarrow \hspace{0.3cm} d = 2\sqrt {E_{\rm S}} \cdot \sin{\pi}/{M })\hspace{0.05cm}.$$ |
| − | |||
| − | + | *This results in the following numerical values: | |
:$$M = 8\hspace{-0.09cm}: \hspace{0.2cm}d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.765} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm},$$ | :$$M = 8\hspace{-0.09cm}: \hspace{0.2cm}d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.765} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm},$$ | ||
:$$M = 16\hspace{-0.09cm}: \hspace{0.2cm} d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.390} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm}.$$ | :$$M = 16\hspace{-0.09cm}: \hspace{0.2cm} d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.390} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Using the result from subtask '''(3)''', we obtain with the equation given in front: |
:$$p_{\rm S} \le p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | :$$p_{\rm S} \le p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | ||
| − | + | *With $E_{\rm S}/N_0 = 50$ ⇒ $(2E_{\rm S}/N_0)^{\rm 0.5} = 10$ it follows: | |
| − | :$$M = 8\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.383 )= 2 \cdot {\rm Q} ( 3.83 ) \approx \underline{ | + | :$$M = 8\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.383 )= 2 \cdot {\rm Q} ( 3.83 ) \approx \underline{0.014 \%} \hspace{0.05cm},$$ |
| − | :$$ M = 16\hspace{-0.09cm}: \hspace{0.2cm} p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.195 )= 2 \cdot {\rm Q} ( 1.95 ) \approx \underline{6 \ | + | :$$ M = 16\hspace{-0.09cm}: \hspace{0.2cm} p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.195 )= 2 \cdot {\rm Q} ( 1.95 ) \approx \underline{6 \%} \hspace{0.05cm}.$$ |
| − | + | *Thus, the symbol error probability becomes larger and larger as $M$ increases, assuming constant $E_{\rm S}/N_0$, as in this case. | |
| + | |||
| + | *The most favorable value would result for $M = 2$ (the factor $2$ of the Union Bound is then not necessary) as follows | ||
:$$M = 2\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} = p_{\rm S} = {\rm Q} ( 10 ) \approx { 10^{-23}}.$$ | :$$M = 2\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} = p_{\rm S} = {\rm Q} ( 10 ) \approx { 10^{-23}}.$$ | ||
| − | + | *Thus, multi-level PSK would not make sense if there were not other reasons for its use, which will be discussed in subtask '''(6)'''. | |
| − | |||
| − | |||
| − | + | '''(5)''' Correct is <u>YES</u>. The graph shows the constellation for "8–PSK" and "16–PSK". | |
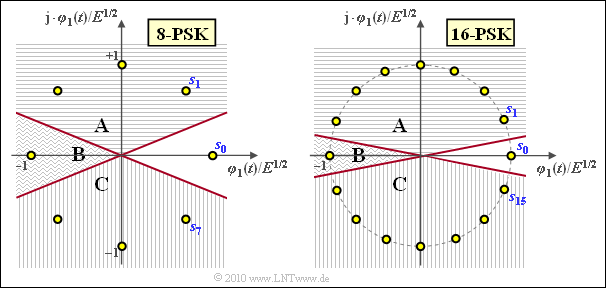
| − | + | [[File:P_ID2071__Dig_A_4_14e.png|right|frame|For the interpretation of the Union Bound at the "$\rm M–PSK$"]] | |
| − | + | ||
| − | + | *Each valid under the assumption that $\boldsymbol{s}_0$ was transmitted. | |
| + | *The contour lines of the AWGN PDF are then circles around $\boldsymbol{s}_0$. | ||
| − | '''(6)''' | + | |
| − | :$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) = 10^{-4} | + | The following statements are valid: |
| + | # The actual error probability $p_{\rm S}$ is composed of the components $\rm A$, $\rm B$ and $\rm C$. | ||
| + | # On the other hand, the "Union Bound" results from $\rm A+B$ $($falsification into the symbol $\boldsymbol{s}_1)$ plus $\rm C+B$ $($falsification into the symbol $\boldsymbol{s}_{M-1})$. | ||
| + | # Thus, $p_{\rm S} = p_{\rm UB}-B$ always holds, but the larger $M$ is, the smaller the fraction $\rm B$ is. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' For verification we assume $p_{\rm B} = 10^{\rm –4}$. | ||
| + | |||
| + | *From this follows for $M = 2$ and $M = 4$: | ||
| + | :$$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) = 10^{-4}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} | ||
\sqrt{ { {2E_{\rm B}}}/{ N_0} } \approx 3.72 | \sqrt{ { {2E_{\rm B}}}/{ N_0} } \approx 3.72 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *On the other hand, with the given equation for $M = 8$: | |
| − | :$$p_{\rm B} \hspace{-0.1cm} \ \le \ \hspace{-0.1cm} \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right )= | + | :$$p_{\rm B} \hspace{-0.1cm} \ \le \ \hspace{-0.1cm} \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right )= {2}/{3} \cdot {\rm Q} \left ( \sqrt{3} \cdot 0.383 \cdot 3.72 \right ) \approx {2}/{3} \cdot {\rm Q} \left ( 2.46 \right ) \approx 0.46 \% |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Accordingly, for $M = 16$ ⇒ ${\rm log}_2 (M) = 4$ is obtained: | |
| − | :$$p_{\rm B} = {2}/{4} \cdot {\rm Q} \left ( \sqrt{4} \cdot 0.195 \cdot 3.72 \right ) \approx {1}/{2} \cdot {\rm Q} \left ( 1.45 \right ) \approx | + | :$$p_{\rm B} = {2}/{4} \cdot {\rm Q} \left ( \sqrt{4} \cdot 0.195 \cdot 3.72 \right ) \approx {1}/{2} \cdot {\rm Q} \left ( 1.45 \right ) \approx 4.8 \% |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Thus, The <u>statements 1 and 4</u> are correct: | |
| + | *Thus, the main advantage of a higher-level PSK is not the lower bit error rate, but the lower demand on the very expensive resource "bandwidth". | ||
| + | |||
| + | *It should also be noted that the results are completely different when a (highly) distorting channel is present, as is common in "wireline transmission technology". | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.4 Coherent Demodulation^]] |
Latest revision as of 20:31, 1 September 2022
Now a signal set $\{s_i(t)\}$ is considered, which is limited to the time domain $0 ≤ t ≤ T$. The index $i$ runs through the values $0, \ \text{...} \ , M-1$:
- $$s_i(t) = A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) \hspace{0.05cm}.$$
- This is a "phase modulation" with $M$ signal shapes.
- This modulation process is also called "$\rm M–PSK$". $M$ is usually a power of two.
The graphic shows the signal space constellation for $M = 8$ (top) and $M = 16$ (bottom). All signal space points have equal energy $||\boldsymbol{s}_i||^2 = E_{\rm S}$ ("average symbol energy").
The exact calculation of the symbol error probability is difficult for $M ≠ 2$. However, the so-called "Union Bound" can always be given as an upper bound for the symbol error probability $(p_{\rm UB} ≥ p_{\rm S})$:
- $$ p_{\rm UB} = 2 \cdot {\rm Q} \left ( \frac{ d/2}{ \sigma_n}\right ) = 2 \cdot {\rm Q} \left (\sqrt{ \frac{ d^2}{ 2 N_0}}\right ) \hspace{0.05cm}.$$
The following quantities are used here:
- $d$ is the distance between two neighboring points, for example between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$.
- If the decision boundary is exactly centered perpendicular to the line connecting $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$, then $d/2$ is the distance of $\boldsymbol{s}_0$ or $\boldsymbol{s}_1$ from this decision boundary.
- The variance of the AWGN noise is $\sigma_n^2 = N_0/2$.
- The factor of $2$ in the above limit takes into account that for $M > 2$ each signal space point can be falsified in two directions, e.g. for the "8–PSK" the symbol $\boldsymbol{s}_0$ into the symbol $\boldsymbol{s}_1$ or into the symbol $\boldsymbol{s}_7$.
- ${\rm Q}(x)$ is the complementary Gaussian error function for which the following approximation holds:
- $${\rm Q}(x) \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$
The last subtask deals with the bit error probability. For this, the following bound was given in the "theory section" under the assumption of a "Gray code":
- $$p_{\rm B} \le \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$
However, this equation is only applicable for $M > 4$. In contrast, the exact solution
- for $M = 2$ from the identity with the "BPSK", and
- for $M = 4$ from the fact that the "4–PSK" is identical with the "4–QAM":
- $$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the topic of the chapter "Carrier Frequency Systems with Coherent Demodulation".
- Reference is made in particular to the section "Multi-level Phase Shift Keying".
- The assignment of the $8$ or $16$ symbols to binary sequences of length $3$ or $4$ according to the Gray coding can be taken from the graphic (red labeling).
- When solving the exercise, you can use the following equations:
- $$\cos(\alpha + \beta) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(\alpha ) \cdot \cos( \beta) - \sin(\alpha ) \cdot \sin( \beta)\hspace{0.05cm}, \hspace{0.25cm} 1 - \cos(2\alpha ) = \sin^2(\alpha )\hspace{0.05cm},$$
- $$ \int_{0}^{T} \cos^2 ( 2\pi f_{\rm T}t) \,{\rm d} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{0.15cm}{\rm falls}\hspace{0.15cm} f_{\rm T} \gg 1/T \hspace{0.05cm}.$$
Questions
Solution
- The signal set $\{s_i(t)\}$ can be represented in the band-pass domain with the given trigonometric transformation as follows:
- $$s_i(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos \left ( 2\pi f_{\rm T}t + { 2\pi }/{ M} \cdot i \right ) = A \cdot \cos \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \cos \left ( 2\pi f_{\rm T}t \right )- A \cdot \sin \left ( { 2\pi }/{ M} \cdot i \right ) \cdot \sin \left ( 2\pi f_{\rm T}t \right )\hspace{0.05cm}.$$
- The respective first terms in this difference lead to the signal space point $\boldsymbol{s}_i$, the respective second terms to the basis functions $\varphi_1(t)$ and $\varphi_2(t)$.
- Here it is to be noted that these must be energy normalized in each case:
- $$\int_{0}^{T} \varphi_1 ( t)^2 \,{\rm d} t = \int_{0}^{T} \left [K \cdot \cos( 2\pi f_{\rm T}t)\right ]^2 \,{\rm d} t = 1\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{K^2 \cdot T}{2} = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = \sqrt{2/T } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \varphi_1 ( t) = \sqrt{2/T } \cdot \cos( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$
- Using the same arithmetic, we arrive at the second basis function:
- $$\varphi_2 ( t) = -\sqrt{2/T } \cdot \sin( 2\pi f_{\rm T}t)\hspace{0.05cm}.$$
(2) Solutions 1 and 4 are correct:
- Using the basis functions just calculated, the signal set $s_i(t)$ can be represented as follows $($again, limited to the range $0 ≤ t ≤ T)$:
- $$s_i(t) = A \cdot \sqrt{T/2 } \cdot \cos ( 2\pi \cdot i /M ) \cdot \varphi_1 ( t)+ A \cdot \sqrt{T/2 } \cdot \sin ( 2\pi \cdot i /M ) \cdot \varphi_2 ( t) \hspace{0.05cm}.$$
- With the energy $E = 0.5 \cdot A^2 \cdot T$, which is the same for all $M$ points and which is also the average signal energy per symbol $(E_{\rm S})$, the above equation is
- $$s_i(t) = s_{{\rm I}i} \cdot \varphi_1 ( t)+ s_{{\rm Q}i} \cdot \varphi_2 ( t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} s_{{\rm I}i} = \sqrt{E_{\rm S} }\cdot \cos ( 2\pi \cdot i /M )\hspace{0.05cm},\hspace{0.2cm} s_{{\rm Q}i} = \sqrt{E_{\rm S} }\cdot \sin ( 2\pi \cdot i /M )\hspace{0.05cm}. $$
- The signal space points sketched in the front graph for $M = 8$ resp. $M = 16$, can be represented in exactly this way.
(3) Since the distance from one to the nearest point is the same for all $i$, we can calculate $d$, for example, from the signal space points $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$.
- In doing so, consider the sketch below. According to the "Pythagorean theorem":
- $$d_{\rm norm}^2 \hspace{-0.01cm}=\hspace{-0.01cm} \sin^2(\frac{2\pi}{M}) + [1- \cos(\frac{2\pi}{M})]^2 $$
- $$\Rightarrow \hspace{0.3cm} d_{\rm norm}^2 \hspace{-0.01cm}=\hspace{-0.01cm} 2 \cdot [1- \cos( \frac{2\pi}{M} )] = 4 \cdot \sin^2(\pi/M )\hspace{0.05cm} $$
- $$\Rightarrow \hspace{0.3cm} d_{\rm norm}= 2 \cdot \sin({\pi}/{M }) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} d = 2\sqrt {E_{\rm S}} \cdot \sin{\pi}/{M })\hspace{0.05cm}.$$
- This results in the following numerical values:
- $$M = 8\hspace{-0.09cm}: \hspace{0.2cm}d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.765} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm},$$
- $$M = 16\hspace{-0.09cm}: \hspace{0.2cm} d \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \underline{0.390} \cdot \sqrt {E_{\rm S} } \hspace{0.05cm}.$$
(4) Using the result from subtask (3), we obtain with the equation given in front:
- $$p_{\rm S} \le p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$
- With $E_{\rm S}/N_0 = 50$ ⇒ $(2E_{\rm S}/N_0)^{\rm 0.5} = 10$ it follows:
- $$M = 8\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.383 )= 2 \cdot {\rm Q} ( 3.83 ) \approx \underline{0.014 \%} \hspace{0.05cm},$$
- $$ M = 16\hspace{-0.09cm}: \hspace{0.2cm} p_{\rm UB} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \cdot {\rm Q} ( 10 \cdot 0.195 )= 2 \cdot {\rm Q} ( 1.95 ) \approx \underline{6 \%} \hspace{0.05cm}.$$
- Thus, the symbol error probability becomes larger and larger as $M$ increases, assuming constant $E_{\rm S}/N_0$, as in this case.
- The most favorable value would result for $M = 2$ (the factor $2$ of the Union Bound is then not necessary) as follows
- $$M = 2\hspace{-0.09cm}: \hspace{0.2cm}p_{\rm UB} = p_{\rm S} = {\rm Q} ( 10 ) \approx { 10^{-23}}.$$
- Thus, multi-level PSK would not make sense if there were not other reasons for its use, which will be discussed in subtask (6).
(5) Correct is YES. The graph shows the constellation for "8–PSK" and "16–PSK".
- Each valid under the assumption that $\boldsymbol{s}_0$ was transmitted.
- The contour lines of the AWGN PDF are then circles around $\boldsymbol{s}_0$.
The following statements are valid:
- The actual error probability $p_{\rm S}$ is composed of the components $\rm A$, $\rm B$ and $\rm C$.
- On the other hand, the "Union Bound" results from $\rm A+B$ $($falsification into the symbol $\boldsymbol{s}_1)$ plus $\rm C+B$ $($falsification into the symbol $\boldsymbol{s}_{M-1})$.
- Thus, $p_{\rm S} = p_{\rm UB}-B$ always holds, but the larger $M$ is, the smaller the fraction $\rm B$ is.
(6) For verification we assume $p_{\rm B} = 10^{\rm –4}$.
- From this follows for $M = 2$ and $M = 4$:
- $$p_{\rm B} ={\rm Q} \left ( \sqrt{ { {2E_{\rm B}}}/{ N_0} }\right ) = 10^{-4}$$
- $$\Rightarrow \hspace{0.3cm} \sqrt{ { {2E_{\rm B}}}/{ N_0} } \approx 3.72 \hspace{0.05cm}.$$
- On the other hand, with the given equation for $M = 8$:
- $$p_{\rm B} \hspace{-0.1cm} \ \le \ \hspace{-0.1cm} \frac{2}{{\rm log_2} \hspace{0.05cm}(M)} \cdot {\rm Q} \left ( \sqrt{{\rm log_2} \hspace{0.05cm}(M)} \cdot \sin ({ \pi}/{ M}) \cdot \sqrt{ { {2E_{\rm S}}}/{ N_0} }\right )= {2}/{3} \cdot {\rm Q} \left ( \sqrt{3} \cdot 0.383 \cdot 3.72 \right ) \approx {2}/{3} \cdot {\rm Q} \left ( 2.46 \right ) \approx 0.46 \% \hspace{0.05cm}.$$
- Accordingly, for $M = 16$ ⇒ ${\rm log}_2 (M) = 4$ is obtained:
- $$p_{\rm B} = {2}/{4} \cdot {\rm Q} \left ( \sqrt{4} \cdot 0.195 \cdot 3.72 \right ) \approx {1}/{2} \cdot {\rm Q} \left ( 1.45 \right ) \approx 4.8 \% \hspace{0.05cm}.$$
Thus, The statements 1 and 4 are correct:
- Thus, the main advantage of a higher-level PSK is not the lower bit error rate, but the lower demand on the very expensive resource "bandwidth".
- It should also be noted that the results are completely different when a (highly) distorting channel is present, as is common in "wireline transmission technology".