Difference between revisions of "Aufgaben:Exercise 2.6: Modified MS43 Code"
| (16 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Block_Coding_with_4B3T_Codes |
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_Z_1_4.png|right|frame|Code table of the MMS43 code ]] |
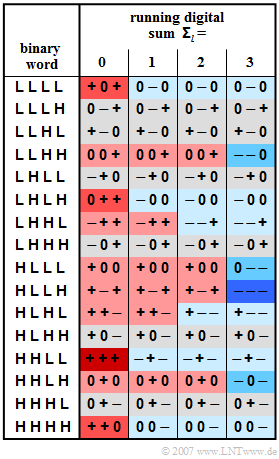
| − | + | For ISDN data transmission, the '''MMS43 code''' ("'''M'''odified '''M'''onitored '''S'''um '''4'''B'''3'''T") is used in Germany and Belgium on the so-called $\rm {U_{K0}}$ interface, which describes the transmission path between the exchange and home. This is a 4B3T code with four code tables, which are used for coding according to the running digital sum (after $l$ blocks): | |
| − | :$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu | + | :$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu.$$ |
| − | + | ${\it \Sigma}_{0} = 0$ is used for initialization. | |
| − | |||
| − | |||
| − | |||
| + | The colorings in the table mean: | ||
| + | *If the running digital sum does not change $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, a field is grayed out. | ||
| + | *An increase $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ is highlighted in red, a decrease $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ in blue. | ||
| − | + | *The more intense the coloring, the larger the change. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | Notes: |
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Block_Coding_with_4B3T_Codes|"Block Coding with 4B3T Codes"]]. | ||
| + | |||
| + | *The binary symbols are denoted by $\rm L$ ("Low") and $\rm H$ ("High") in this learning tutorial. Often you can find the binary symbols $\rm L$ and $\rm 0$ $($instead of $\rm H)$ in the literature. Sometimes, however, $\rm L$ corresponds to our $\rm H$ and $\rm 0$ to $\rm L$. | ||
| − | * | + | *To avoid such confusion and to prevent the $\rm 0$ from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers. |
| − | === | + | |
| + | *You can check the results with the (German language) SWF applet [[Applets:4B3T-Codes|"Principle of 4B3T coding"]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Why is a 4B3T code used for ISDN instead of the redundancy-free binary code? |
|type="[]"} | |type="[]"} | ||
| − | - 4B3T | + | - 4B3T is always better than the redundancy-free binary code. |
| − | + | + | + The transmitted signal should be DC signal free because of $H_{\rm K}(f=0) = 0$. |
| − | + | + | + A smaller baud rate allows longer cable length. |
| − | { | + | {Code the binary sequence $\rm HHLL\hspace{0.08cm} LHLL\hspace{0.08cm} LHHL\hspace{0.08cm} HLHL$ $($with ${\it \Sigma}_{0} = 0)$ . <br>What is the amplitude coefficient of the third ternary symbol of the fourth block? |
|type="{}"} | |type="{}"} | ||
$a_{12} \ = \ $ { -1.03--0.97 } | $a_{12} \ = \ $ { -1.03--0.97 } | ||
| − | { | + | {Determine the Markov diagram for the transition from ${\it \Sigma}_{l}$ to ${\it \Sigma}_{l+1}$. What are the transition probabilities? |
|type="{}"} | |type="{}"} | ||
| − | $ {\Pr}(\ | + | $ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $ { 0.375 3% } |
| − | $ {\Pr}(\ | + | $ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $ { 0.1875 3% } |
| − | $ {\Pr}(\ | + | $ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ = \ $ { 0 3% } |
| − | { | + | {What properties follow from the Markov diagram? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Equal probabilities: ${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}(\Sigma_{l} = 3)$. |
| − | + | + | + ${\rm Pr}({\it \Sigma}_{l} = 0) = {\rm Pr}({\it \Sigma}_{l} = 3)$ and ${\rm Pr}({\it \Sigma}_{l} = 1) = {\rm Pr}({\it \Sigma}_{l} = 2)$ are valid. |
| − | + | + | + The extreme values $({\it \Sigma}_{l} = 0$ and ${\it \Sigma}_{l} = 3)$ occur less frequently than the inner values $({\it \Sigma}_{l} = 1$ and ${\it \Sigma}_{l} = 2)$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Statements 2 and 3</u> are correct: |
| − | + | *The first statement, on the other hand, is not true: For example, the AWGN ("Additive White Gaussian Noise") channel with a 4B3T code results in a much larger symbol error probability due to the ternary decision compared to the redundancy-free binary code. | |
| − | + | ||
| − | + | *The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a "telephone channel". | |
| − | |||
| − | |||
| − | |||
| − | + | *The $25 \%$ smaller baud rate $(1/T)$ of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines (strong increase in attenuation with frequency). | |
| + | |||
| + | *For a given line attenuation, a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal. | ||
| − | |||
| − | ''' | + | [[File:P_ID1341__Dig_A_2_6c.png|right|frame|Markov diagram for the MMS43 code]] |
| + | '''(2)''' The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$: | ||
| − | + | *$\rm HHLL$ ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$, | |
| + | *$\rm LHLL$ ⇒ $– + 0 \hspace{0.2cm}({\it\Sigma}_{2} = 3)$, | ||
| + | *$\rm LHHL$ ⇒ $– – + \hspace{0.2cm}({\it\Sigma}_{3} = 2)$, | ||
| + | *$\rm HLHL$ ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$. | ||
| − | + | Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$. | |
| − | |||
| − | ${\ | ||
| − | |||
| − | |||
| + | '''(3)''' From the coloring of the code table, the Markov diagram can be obtained. | ||
| + | *From it, one can read the transition probabilities we are looking for: | ||
| + | :$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$ | ||
| + | :$$ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 0)= 3/16 \ \underline{= 0.1875},$$ | ||
| + | :$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ \underline{= 0}.$$ | ||
| + | '''(4)''' <u>Statements 2 and 3</u> are correct: | ||
| + | *Statement 1 is false, recognizable by the asymmetries in the Markov diagram. | ||
| − | + | *On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$". | |
| − | + | ||
| − | + | *In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0)$ we write $ {\rm Pr}(0)$ in a simplified way. | |
| − | + | ||
| − | + | *Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram: | |
| − | |||
| − | |||
:$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$ | :$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$ | ||
| − | + | *From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further: | |
:$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$ | :$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$ | ||
| − | + | :This calculation is based on the "sum of incoming arrows in state $0$". | |
| + | |||
| + | One could also give equations for the other three states, but they all give the same result: | ||
:$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | :$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | ||
:$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | :$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | ||
:$${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$ | :$${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$ | ||
| − | + | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 104: | Line 112: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^2.3 Blockwise 4B3T Coding^]] |
Latest revision as of 16:56, 24 October 2022
For ISDN data transmission, the MMS43 code ("Modified Monitored Sum 4B3T") is used in Germany and Belgium on the so-called $\rm {U_{K0}}$ interface, which describes the transmission path between the exchange and home. This is a 4B3T code with four code tables, which are used for coding according to the running digital sum (after $l$ blocks):
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu.$$
${\it \Sigma}_{0} = 0$ is used for initialization.
The colorings in the table mean:
- If the running digital sum does not change $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, a field is grayed out.
- An increase $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ is highlighted in red, a decrease $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ in blue.
- The more intense the coloring, the larger the change.
Notes:
- The exercise belongs to the chapter "Block Coding with 4B3T Codes".
- The binary symbols are denoted by $\rm L$ ("Low") and $\rm H$ ("High") in this learning tutorial. Often you can find the binary symbols $\rm L$ and $\rm 0$ $($instead of $\rm H)$ in the literature. Sometimes, however, $\rm L$ corresponds to our $\rm H$ and $\rm 0$ to $\rm L$.
- To avoid such confusion and to prevent the $\rm 0$ from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers.
- You can check the results with the (German language) SWF applet "Principle of 4B3T coding".
Questions
Solution
- The first statement, on the other hand, is not true: For example, the AWGN ("Additive White Gaussian Noise") channel with a 4B3T code results in a much larger symbol error probability due to the ternary decision compared to the redundancy-free binary code.
- The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a "telephone channel".
- The $25 \%$ smaller baud rate $(1/T)$ of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines (strong increase in attenuation with frequency).
- For a given line attenuation, a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal.
(2) The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$:
- $\rm HHLL$ ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$,
- $\rm LHLL$ ⇒ $– + 0 \hspace{0.2cm}({\it\Sigma}_{2} = 3)$,
- $\rm LHHL$ ⇒ $– – + \hspace{0.2cm}({\it\Sigma}_{3} = 2)$,
- $\rm HLHL$ ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$.
Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$.
(3) From the coloring of the code table, the Markov diagram can be obtained.
- From it, one can read the transition probabilities we are looking for:
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 0)= 3/16 \ \underline{= 0.1875},$$
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ \underline{= 0}.$$
(4) Statements 2 and 3 are correct:
- Statement 1 is false, recognizable by the asymmetries in the Markov diagram.
- On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$".
- In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0)$ we write $ {\rm Pr}(0)$ in a simplified way.
- Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram:
- $${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$
- From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further:
- $${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$
- This calculation is based on the "sum of incoming arrows in state $0$".
One could also give equations for the other three states, but they all give the same result:
- $${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$