Difference between revisions of "Aufgaben:Exercise 4.4: Extrinsic L-values at SPC"
| (45 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} |
| − | [[File: | + | [[File:EN_KC_A_4_4.png|right|frame|Suitable auxiliary table]] |
| − | + | We consider again the [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes|"single parity–check code"]]. In such a ${\rm SPC} \ (n, \, n-1, \, 2)$ the $n$ bits of a code word $\underline{x}$ come from the $k = n -1$ bits from the source sequence $\underline{u}$ and only a single check bit $p$ is added, such that the number of "ones" in the code word $\underline{x}$ is even: | |
| − | :$$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0. | + | :$$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = |
| − | \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0. | + | \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}. $$ |
| − | + | The extrinsic information about the $i$th code bit is formed over all other bits $(j ≠ i)$. Therefore we write for the code word shorter by one bit: | |
| − | :$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0. | + | :$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$ |
| − | + | The extrinsic L–value over the $i$th code symbol reads with the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Hamming weight"]] $w_{\rm H}$ of the truncated sequence $\underline{x}^{(-i)}$: | |
| − | :$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm | + | :$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *If the probability in the numerator is greater than that in the denominator, then $L_{\rm E}(i) > 0$ and thus the a-posteriori L–value $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ magnified, that is tends to be affected in the direction of the symbol $x_i = 0$. | |
| + | |||
| + | *If $L_{\rm E}(i) < 0$ then there is much to be said for $x_i = 1$ from the point of view of the other symbols $(j ≠ i)$. | ||
| − | + | ||
| + | Only the $\text{SPC (4, 3, 4)}$ is treated, where for the probabilities $p_i = {\rm Pr}(x_i = 1)$ holds: | ||
:$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} | :$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} | ||
p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} | p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} | ||
| Line 21: | Line 24: | ||
p_4 = 0.6 \hspace{0.05cm}.$$ | p_4 = 0.6 \hspace{0.05cm}.$$ | ||
| − | + | From this the a-priori log likelihood ratios result to: | |
:$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} | :$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} | ||
\right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} | \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} | ||
| Line 27: | Line 30: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | <u>Hints:</u> | ||
| + | *This exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder|"Soft–in Soft–out Decoder"]]. | ||
| + | |||
| + | *Reference is made in particular to the section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"Calculation of the extrinsic log likelihood ratios"]]. | ||
| + | |||
| + | * In the table are given for $p_i = 0$ to $p_i = 1$ with step size $0.1$ $($column 1$)$: | ||
| + | ::In column 2: the probability $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$, | ||
| + | ::in column 3: the values for $1 - 2p_i$, | ||
| + | ::in column 4: the a-priori log likelihood ratios $L_i = \ln {\big [(1 - p_i)/p_ i \big ]} = L_{\rm A}(i)$. | ||
| + | |||
| + | * The "hyperbolic tangent" $(\tanh)$ of $L_i/2$ is identical to $1-2p_i$ ⇒ column 3. | ||
| + | |||
| + | * In [[Aufgaben:Exercise_4.4Z:_Supplement_to_Exercise_4.4|$\text{Exercise 4.4Z}$]] it is shown that for the extrinsic L–value can also be written: | ||
| + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} | ||
| + | {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {It holds $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$. From this, calculate the a-priori log likelihood ratios of the $\text{SPC (4, 3, 4)}$ for bit 1 and bit 2. |
| + | |type="{}"} | ||
| + | $L_{\rm A}(i = 1) \ = \ ${ 1.386 3% } | ||
| + | $L_{\rm A}(i = 2) \ = \ ${ -2.26291--2.13109 } | ||
| + | |||
| + | {What are the extrinsic log likelihood ratios for bit 1 and bit 2. | ||
| + | |type="{}"} | ||
| + | $L_{\rm E}(i = 1) \ = \ ${ 0.128 3% } | ||
| + | $L_{\rm E}(i = 2) \ = \ ${ -0.09888--0.09312 } | ||
| + | |||
| + | {What are the relationships between $p_j$ and $L_j = L_{\rm A}(j)$? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + It holds $p_j = 1/(1 + {\rm e}^ {L_j})$. |
| − | - | + | + It holds $1-2p_j = ({\rm e}^ {L_j} - 1) \ / \ ({\rm e}^ {L_j} + 1)$. |
| + | + It holds $1-2p_j = \tanh {(L_j/2)}$. | ||
| − | { | + | {It is further $p_1 = 0.2, \ p_2 = 0.9, \ p_3, \ p_4 = 0.6$. Calculate the extrinsic log likelihood ratios for bit 3 and bit 4. Use different equations for this purpose. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $L_{\rm E}(i = 3) \ = \ ${ 0.193 3% } |
| + | $L_{\rm E}(i = 4) \ = \ ${ -0.40067--0.37733 } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the a-priori log likelihood ratios of the first two bits of the code word: |
| − | '''(2)''' | + | :$$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} |
| − | '''(3)''' | + | \hspace{0.05cm},$$ |
| − | '''(4)''' | + | :$$L_{\rm A}(i = 2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_2}{p_2} \right ] = {\rm ln} \hspace{0.1cm} 1/9 \hspace{0.15cm}\underline{= -2.197} |
| − | '''( | + | \hspace{0.05cm}.$$ |
| + | |||
| + | *The values can be read from the fourth column of the table attached to the information page. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' To calculate the extrinsic L–value over the $i$th bit, only the information about the other three bits $(j ≠ i)$ may be used. With the given equation holds: | ||
| + | :$$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *For the product, we obtain according to the third column of the [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC|$\rm table$]]: | ||
| + | :$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
| + | (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 | ||
| + | \hspace{0.05cm}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *In terms of bit 2, one obtains accordingly: | ||
| + | :$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
| + | (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 | ||
| + | \hspace{0.05cm}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' For the a-priori L– value holds: | ||
| + | :$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} | ||
| + | \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} | ||
| + | \right ]\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } | ||
| + | \hspace{0.05cm} .$$ | ||
| + | |||
| + | *Thus also applies: | ||
| + | :$$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } | ||
| + | = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$ | ||
| + | |||
| + | *Multiplying the numerator and denominator by ${\rm e}^{-L_j/2}$, we get: | ||
| + | :$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$ | ||
| + | |||
| + | *Thus <u>all proposed solutions</u> are correct. | ||
| + | |||
| + | *The function "hyperbolic tangent" can be found, for example, in tabular form in formula collections or in the last column of the table given in front. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' We first calculate $L_{\rm E}(i = 3)$ in the same way as in subtask '''(2)''': | ||
| + | :$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
| + | (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 | ||
| + | \hspace{0.05cm}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *We calculate the extrinsic L–value with respect to the last bit according to the equation | ||
| + | :$$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} | ||
| + | {\rm with} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *This results in accordance with the above [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC|$\rm table$]]: | ||
| + | :$$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | L_1/2 = +0.693 \hspace{0.2cm} | ||
| + | \Rightarrow \hspace{0.2cm} | ||
| + | {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} | ||
| + | = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$ | ||
| + | :$$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | L_2/2 = -1.099\hspace{0.2cm} | ||
| + | \Rightarrow \hspace{0.2cm} | ||
| + | {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} | ||
| + | = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$ | ||
| + | :$$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| + | L_3/2 = +0.419 \hspace{0.2cm} | ||
| + | \Rightarrow \hspace{0.2cm} | ||
| + | {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} | ||
| + | = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$ | ||
| + | |||
| + | *The final result is thus: | ||
| + | :$$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 -0.192}{1 +0.192}\hspace{0.15cm}\underline{= -0.389} | ||
| + | \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^4.1 Soft–in Soft–out Decoder^]] |
Latest revision as of 16:25, 23 January 2023
We consider again the "single parity–check code". In such a ${\rm SPC} \ (n, \, n-1, \, 2)$ the $n$ bits of a code word $\underline{x}$ come from the $k = n -1$ bits from the source sequence $\underline{u}$ and only a single check bit $p$ is added, such that the number of "ones" in the code word $\underline{x}$ is even:
- $$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}. $$
The extrinsic information about the $i$th code bit is formed over all other bits $(j ≠ i)$. Therefore we write for the code word shorter by one bit:
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
The extrinsic L–value over the $i$th code symbol reads with the "Hamming weight" $w_{\rm H}$ of the truncated sequence $\underline{x}^{(-i)}$:
- $$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$
- If the probability in the numerator is greater than that in the denominator, then $L_{\rm E}(i) > 0$ and thus the a-posteriori L–value $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ magnified, that is tends to be affected in the direction of the symbol $x_i = 0$.
- If $L_{\rm E}(i) < 0$ then there is much to be said for $x_i = 1$ from the point of view of the other symbols $(j ≠ i)$.
Only the $\text{SPC (4, 3, 4)}$ is treated, where for the probabilities $p_i = {\rm Pr}(x_i = 1)$ holds:
- $$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} p_3 = 0.3 \hspace{0.05cm}, \hspace{0.3cm} p_4 = 0.6 \hspace{0.05cm}.$$
From this the a-priori log likelihood ratios result to:
- $$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} \right ] \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the section "Calculation of the extrinsic log likelihood ratios".
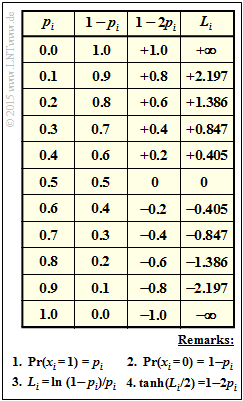
- In the table are given for $p_i = 0$ to $p_i = 1$ with step size $0.1$ $($column 1$)$:
- In column 2: the probability $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$,
- in column 3: the values for $1 - 2p_i$,
- in column 4: the a-priori log likelihood ratios $L_i = \ln {\big [(1 - p_i)/p_ i \big ]} = L_{\rm A}(i)$.
- The "hyperbolic tangent" $(\tanh)$ of $L_i/2$ is identical to $1-2p_i$ ⇒ column 3.
- In $\text{Exercise 4.4Z}$ it is shown that for the extrinsic L–value can also be written:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) \hspace{0.05cm}.$$
Questions
Solution
- $$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} \hspace{0.05cm},$$
- $$L_{\rm A}(i = 2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_2}{p_2} \right ] = {\rm ln} \hspace{0.1cm} 1/9 \hspace{0.15cm}\underline{= -2.197} \hspace{0.05cm}.$$
- The values can be read from the fourth column of the table attached to the information page.
(2) To calculate the extrinsic L–value over the $i$th bit, only the information about the other three bits $(j ≠ i)$ may be used. With the given equation holds:
- $$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} \hspace{0.05cm}.$$
- For the product, we obtain according to the third column of the $\rm table$:
- $$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} \hspace{0.05cm}.$$
- In terms of bit 2, one obtains accordingly:
- $$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} \hspace{0.05cm}.$$
(3) For the a-priori L– value holds:
- $$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } \hspace{0.05cm} .$$
- Thus also applies:
- $$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$
- Multiplying the numerator and denominator by ${\rm e}^{-L_j/2}$, we get:
- $$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$
- Thus all proposed solutions are correct.
- The function "hyperbolic tangent" can be found, for example, in tabular form in formula collections or in the last column of the table given in front.
(4) We first calculate $L_{\rm E}(i = 3)$ in the same way as in subtask (2):
- $$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} \hspace{0.05cm}.$$
- We calculate the extrinsic L–value with respect to the last bit according to the equation
- $$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm with} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \hspace{0.05cm}.$$
- This results in accordance with the above $\rm table$:
- $$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1/2 = +0.693 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$
- $$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2/2 = -1.099\hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$
- $$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3/2 = +0.419 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$
- The final result is thus:
- $$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 -0.192}{1 +0.192}\hspace{0.15cm}\underline{= -0.389} \hspace{0.05cm}.$$