Difference between revisions of "Aufgaben:Exercise 4.4Z: Supplement to Exercise 4.4"
| (51 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Soft-in_Soft-Out_Decoder}} |
| − | [[File:P_ID2994__KC_Z_4_4_v3.png |right|frame| | + | [[File:P_ID2994__KC_Z_4_4_v3.png |right|frame|Hamming weights $w_{\rm H}(\underline{x})$, <br>sequence probabilities ${\rm Pr}(\underline{x})$ ]] |
| − | + | The information theorist [https://en.wikipedia.org/wiki/Robert_G._Gallager $\text{Robert G. Gallager}$] dealt already in 1963 with the following problem: | |
| − | * | + | * Given a random vector $\underline{x} = (x_1, \, x_2, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_n)$ with $n$ binary elements $x_i ∈ \{0, \, 1\}$. |
| − | |||
| − | |||
| − | |||
| + | * Known are all probabilities $p_i = {\rm Pr}(x_i = 1)$ and $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ with index $i = 1, \hspace{-0.04cm}\text{ ...} \hspace{0.08cm} ,\ n$. | ||
| − | + | * What we are looking for is the probability that the number of "ones" in this vector is even. | |
| − | * | ||
| − | |||
| − | |||
| + | * Or expressed using the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Hamming weight"]]: What is the probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$? | ||
| − | + | ||
| − | :$$\ | + | The graph illustrates the task for the example $n = 4$ and $p_1 = 0.2$, $p_2 = 0.9$, $p_3 = 0.3$ and $p_4 = 0.6$. |
| + | * For the row highlighted in green ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ holds $w_{\rm H}(\underline{x}) = 2$ and | ||
| + | :$${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$ | ||
| + | * Blue font means "$w_{\rm H}(\underline{x})$ is even". Red font stands for "$w_{\rm H}(\underline{x})$ is odd." | ||
| + | |||
| + | *The probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$ is the sum of the blue numbers in the last column. | ||
| + | |||
| + | *The sum of the red numbers gives ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ odd}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$. | ||
| + | |||
| + | |||
| + | Gallager solved the problem in an analytical way: | ||
| + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \right ] | ||
\hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$ | \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$ | ||
| − | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm | + | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} |
\right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$ | \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$ | ||
| + | |||
| + | Here the following auxiliary variable is used: | ||
| + | :$$\pi = \prod\limits_{i =1}^{n} \hspace{0.25cm}(1-2p_i) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | One applies the equation, for example, to calculate the extrinsic L–values of a "single parity–check code". | ||
| + | |||
| + | Indeed, as already pointed out in [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC| $\text{Exercise 4.4}$]] the extrinsic log likelihood ratio with Hamming–weight $w_{\rm H}$ is the truncated sequence $\underline{x}^{(-i)}$: | ||
| + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Here it is taken into account that for $L_{\rm E}(i)$ one may refer only to the other symbols $(j ≠ i)$ : | ||
| + | :$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <u>Hints:</u> | ||
| + | *This exercise belongs to the chapter [[Channel_Coding/Soft%E2%80%93in_Soft%E2%80%93out_Decoder|"Soft–in Soft–out Decoder"]]. | ||
| + | |||
| + | *Reference is made in particular to the section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_log_likelihood_ratios|"For calculating the extrinsic log likelihood ratios"]]. | ||
| + | |||
| + | *The exercise is intended as a supplement to [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC| $\text{Exercise 4.4}$]] . | ||
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {We consider the vector $\underline{x} = (x_1, \, x_2) \ \Rightarrow \ n = 2$ with $x_i ∈ \{0, \, 1\}$ and $p_1 = 0.2, \ p_2 = 0.9$. <br>What is the probability that $\underline{x}$ contains an even number of "ones" ? |
| − | |type="[] | + | |type="{}"} |
| − | + | ${\rm Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ even}\big ] \ = \ ${ 0.26 3% } | |
| − | |||
| − | { | + | {Compute the same probability for $\underline{x} = (x_1, \, x_2, \, x_3) \ \Rightarrow \ n = 3$ and $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ even}\big ] \ = \ ${ 0.404 3% } |
| + | |||
| + | {Now let be $n = 4$ and $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$. Calculate the following quantities according to Gallager's equation: | ||
| + | |type="{}"} | ||
| + | ${\rm Pr(blue) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ even}\big ] \hspace{0.33cm} = \ ${ 0.5192 3% } | ||
| + | ${\rm Pr(red) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ odd}\big ] \hspace{0.1cm} = \ ${ 0.4808 3% } | ||
| + | $\text{Quotient }Q = {\rm Pr(blau)/Pr(rot)} \hspace{0.4cm} = \ ${ 1.0799 3% } | ||
| + | |||
| + | {What is the extrinsic log likelihood ratio for the symbol $i = 5$ at $\text{SPC (5, 4, 2)}$ with $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6, \ p_5 = 0.9$? | ||
| + | |type="{}"} | ||
| + | $L_{\rm E}(i = 5) \ = \ ${ 0.077 3% } | ||
| + | |||
| + | {How does $L_{\rm E}(i = 5)$ change if we assume $p_5 = 0.1$ instead? | ||
| + | |type="()"} | ||
| + | - $L_{\rm E}(i = 5)$ becomes larger. | ||
| + | - $L_{\rm E}(i = 5)$ becomes smaller. | ||
| + | + $L_{\rm E}(i = 5)$ is not changed compared to subtask '''(4)'''. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | [[File:P_ID2996__KC_Z_4_4a_v1.png|frame|right|Derivation "$w_{\rm H}$ is even" for code length $n = 2$.]] |
| − | ' | + | '''(1)''' According to the adjacent table applies: |
| − | '''( | + | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.10cm}{\rm is \hspace{0.10cm} even}\right ] = |
| − | + | {\rm Pr} \left [w_{\rm H} = 0 \right] + {\rm Pr} \left [w_{\rm H} = 2 \right] | |
| − | '''( | + | \hspace{0.05cm}. $$ |
| − | {{ | + | |
| + | *With the probabilities | ||
| + | :$$p_1 = {\rm Pr} (x_1 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.2\hspace{0.05cm},\hspace{0.3cm}q_1 = {\rm Pr} (x_1 = 0) = 0.8\hspace{0.05cm},$$ | ||
| + | :$$p_2 = {\rm Pr} (x_2 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.9\hspace{0.05cm},\hspace{0.3cm}q_2 = {\rm Pr} (x_2 = 0) = 0.1$$ | ||
| + | |||
| + | :one obtains: | ||
| + | :$${\rm Pr} \left [w_{\rm H}(\underline{x}) = 0\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
| + | {\rm Pr} \left [(x_1 = 0)\cap (x_2 = 0) \right] = q_1 \cdot q_2 = 0.8 \cdot 0.1 | ||
| + | = 0.08 \hspace{0.05cm},$$ | ||
| + | :$${\rm Pr} \left [w_{\rm H}(\underline{x}) = 2\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} | ||
| + | {\rm Pr} \left [(x_1 = 1)\cap (x_2 = 1) \right] = p_1 \cdot p_2 = 0.2 \cdot 0.9 = 0.18$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] = 0.8 + 0.18 \hspace{0.15cm} \underline{= 0.26} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The Gallager's equation provides for the same set of parameters: | ||
| + | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{2} \hspace{0.25cm}(1-2\cdot p_i) = 0.5 + 0.5 \cdot (1 - 2 \cdot 0.2)\cdot (1 - 2 \cdot 0.9) = 0.26 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The equation given by Gallager 1963 was hereby verified for $n = 2$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' In the second table, the four combinations with an even number of "ones" are marked in blue. | ||
| + | [[File:P_ID2997__KC_Z_4_4b_v1.png|right|frame|Derivation "$w_{\rm H}$ is even" for code length $n = 3$.]] | ||
| + | |||
| + | *The occurrence probabilities of each combination are given in the last column. Thus, the result is: | ||
| + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] = 0.056 + 0.216 + 0.006 + 0.126 \hspace{0.15cm} \underline{= 0.404} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The red rows provide the complementary event: | ||
| + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] = 0.024 + 0.504 + 0.014 + 0.054= 0.596 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Gallager's equation again gives the exact same result, although it should be noted that this equation is valid for all $n$ and all arbitrary probabilities: | ||
| + | :$${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{3} \hspace{0.25cm}(1-2\cdot p_i) $$ | ||
| + | :$$\Rightarrow\hspace{0.3cm}{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot (+0.6) \cdot (-0.8) \cdot (+0.4) = 0.404 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' According to the specification page applies: | ||
| + | :$$\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1 - 2 \cdot 0.2) \cdot (1 - 2 \cdot 0.9) \cdot (1 - 2 \cdot 0.3) \cdot (1 - 2 \cdot 0.6) $$ | ||
| + | :$$\Rightarrow\hspace{0.3cm}\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(+0.6) \cdot (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.0384 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *From this can be calculated: | ||
| + | :$${\rm Pr}({\rm blue}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \pi = 0.5 + 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.5192}\hspace{0.05cm},$$ | ||
| + | :$${\rm Pr}({\rm red}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$ | ||
| + | |||
| + | *If you add up the blue and red probabilities on the information page,V you get exactly the values calculated here. For the quotient we get: | ||
| + | :$$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} | ||
| + | \hspace{0.05cm}. $$ | ||
| + | |||
| − | [[ | + | '''(4)''' For the "single parity–check code", the extrinsic log likelihood ratio with respect to the $i^{th}$ bit was specified as follows: |
| + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ||
| + | \hspace{0.05cm},$$ | ||
| + | *Or: | ||
| + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{1+\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)}{1-\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *At $\text{SPC (5, 4, 2}$) ⇒ $n = 5$, this product for $i = 5$ results from the following four factors: | ||
| + | :$$\pi = \prod\limits_{j = 1, \hspace{0.05cm}2, \hspace{0.05cm}3, \hspace{0.05cm}4} \hspace{0.05cm}(1-2\cdot p_j) = | ||
| + | (1-2\cdot p_1) \cdot (1-2\cdot p_2) \cdot (1-2\cdot p_3) \cdot (1-2\cdot p_4) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | The comparison with subtask '''(3)''' shows that $L_{\rm E}(i = 5) = \ln {Q} = \ln {(1.0799)} \ \underline{\approx 0.077}$. | ||
| + | '''(5)''' Correct is the <u>proposed solution 3</u> because the result for $L_{\rm E}(i = 5)$ is independent of $p_5$. | ||
| + | {{ML-Fuß}} | ||
| − | ^]] | + | [[Category:Channel Coding: Exercises|^4.1 Soft–in Soft–out Decoder^]] |
Latest revision as of 15:29, 3 December 2022
The information theorist $\text{Robert G. Gallager}$ dealt already in 1963 with the following problem:
- Given a random vector $\underline{x} = (x_1, \, x_2, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_n)$ with $n$ binary elements $x_i ∈ \{0, \, 1\}$.
- Known are all probabilities $p_i = {\rm Pr}(x_i = 1)$ and $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ with index $i = 1, \hspace{-0.04cm}\text{ ...} \hspace{0.08cm} ,\ n$.
- What we are looking for is the probability that the number of "ones" in this vector is even.
- Or expressed using the "Hamming weight": What is the probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$?
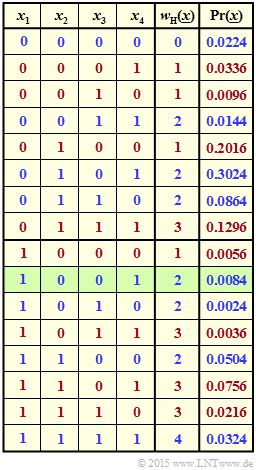
The graph illustrates the task for the example $n = 4$ and $p_1 = 0.2$, $p_2 = 0.9$, $p_3 = 0.3$ and $p_4 = 0.6$.
- For the row highlighted in green ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ holds $w_{\rm H}(\underline{x}) = 2$ and
- $${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$
- Blue font means "$w_{\rm H}(\underline{x})$ is even". Red font stands for "$w_{\rm H}(\underline{x})$ is odd."
- The probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$ is the sum of the blue numbers in the last column.
- The sum of the red numbers gives ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ odd}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$.
Gallager solved the problem in an analytical way:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$
Here the following auxiliary variable is used:
- $$\pi = \prod\limits_{i =1}^{n} \hspace{0.25cm}(1-2p_i) \hspace{0.05cm}.$$
One applies the equation, for example, to calculate the extrinsic L–values of a "single parity–check code".
Indeed, as already pointed out in $\text{Exercise 4.4}$ the extrinsic log likelihood ratio with Hamming–weight $w_{\rm H}$ is the truncated sequence $\underline{x}^{(-i)}$:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$
Here it is taken into account that for $L_{\rm E}(i)$ one may refer only to the other symbols $(j ≠ i)$ :
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the section "For calculating the extrinsic log likelihood ratios".
- The exercise is intended as a supplement to $\text{Exercise 4.4}$ .
Questions
Solution
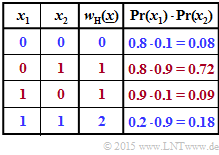
(1) According to the adjacent table applies:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.10cm}{\rm is \hspace{0.10cm} even}\right ] = {\rm Pr} \left [w_{\rm H} = 0 \right] + {\rm Pr} \left [w_{\rm H} = 2 \right] \hspace{0.05cm}. $$
- With the probabilities
- $$p_1 = {\rm Pr} (x_1 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.2\hspace{0.05cm},\hspace{0.3cm}q_1 = {\rm Pr} (x_1 = 0) = 0.8\hspace{0.05cm},$$
- $$p_2 = {\rm Pr} (x_2 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.9\hspace{0.05cm},\hspace{0.3cm}q_2 = {\rm Pr} (x_2 = 0) = 0.1$$
- one obtains:
- $${\rm Pr} \left [w_{\rm H}(\underline{x}) = 0\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr} \left [(x_1 = 0)\cap (x_2 = 0) \right] = q_1 \cdot q_2 = 0.8 \cdot 0.1 = 0.08 \hspace{0.05cm},$$
- $${\rm Pr} \left [w_{\rm H}(\underline{x}) = 2\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr} \left [(x_1 = 1)\cap (x_2 = 1) \right] = p_1 \cdot p_2 = 0.2 \cdot 0.9 = 0.18$$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] = 0.8 + 0.18 \hspace{0.15cm} \underline{= 0.26} \hspace{0.05cm}.$$
- The Gallager's equation provides for the same set of parameters:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{2} \hspace{0.25cm}(1-2\cdot p_i) = 0.5 + 0.5 \cdot (1 - 2 \cdot 0.2)\cdot (1 - 2 \cdot 0.9) = 0.26 \hspace{0.05cm}.$$
- The equation given by Gallager 1963 was hereby verified for $n = 2$.
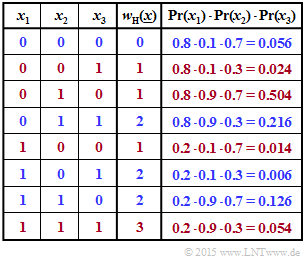
(2) In the second table, the four combinations with an even number of "ones" are marked in blue.
- The occurrence probabilities of each combination are given in the last column. Thus, the result is:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] = 0.056 + 0.216 + 0.006 + 0.126 \hspace{0.15cm} \underline{= 0.404} \hspace{0.05cm}.$$
- The red rows provide the complementary event:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] = 0.024 + 0.504 + 0.014 + 0.054= 0.596 \hspace{0.05cm}.$$
- Gallager's equation again gives the exact same result, although it should be noted that this equation is valid for all $n$ and all arbitrary probabilities:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{3} \hspace{0.25cm}(1-2\cdot p_i) $$
- $$\Rightarrow\hspace{0.3cm}{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot (+0.6) \cdot (-0.8) \cdot (+0.4) = 0.404 \hspace{0.05cm}.$$
(3) According to the specification page applies:
- $$\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1 - 2 \cdot 0.2) \cdot (1 - 2 \cdot 0.9) \cdot (1 - 2 \cdot 0.3) \cdot (1 - 2 \cdot 0.6) $$
- $$\Rightarrow\hspace{0.3cm}\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(+0.6) \cdot (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.0384 \hspace{0.05cm}.$$
- From this can be calculated:
- $${\rm Pr}({\rm blue}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \pi = 0.5 + 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.5192}\hspace{0.05cm},$$
- $${\rm Pr}({\rm red}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$
- If you add up the blue and red probabilities on the information page,V you get exactly the values calculated here. For the quotient we get:
- $$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} \hspace{0.05cm}. $$
(4) For the "single parity–check code", the extrinsic log likelihood ratio with respect to the $i^{th}$ bit was specified as follows:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm},$$
- Or:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{1+\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)}{1-\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)} \hspace{0.05cm}.$$
- At $\text{SPC (5, 4, 2}$) ⇒ $n = 5$, this product for $i = 5$ results from the following four factors:
- $$\pi = \prod\limits_{j = 1, \hspace{0.05cm}2, \hspace{0.05cm}3, \hspace{0.05cm}4} \hspace{0.05cm}(1-2\cdot p_j) = (1-2\cdot p_1) \cdot (1-2\cdot p_2) \cdot (1-2\cdot p_3) \cdot (1-2\cdot p_4) \hspace{0.05cm}.$$
The comparison with subtask (3) shows that $L_{\rm E}(i = 5) = \ln {Q} = \ln {(1.0799)} \ \underline{\approx 0.077}$.
(5) Correct is the proposed solution 3 because the result for $L_{\rm E}(i = 5)$ is independent of $p_5$.