Difference between revisions of "Aufgaben:Exercise 1.6: (7, 4) Hamming Code"
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Examples_of_Binary_Block_Codes |
}} | }} | ||
| − | [[File:P_ID2388__KC_A_1_6_neu.png|right|frame| | + | [[File:P_ID2388__KC_A_1_6_neu.png|right|frame|Code table of the $\text{HC (7, 4)}$]] |
| − | 1962 | + | In 1962, [https://en.wikipedia.org/wiki/Richard_Hamming Richard Wesley Hamming] specified a class of binary block codes that differ in the number $m$ of check bits supplied. The code word length is always $n = 2^m - 1$. The information word consists of $k = n - m$ bits: |
| − | *$m = 2$: | + | *$m = 2$: $\text{(3, 1)}$ Hamming code ⇒ identical to [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|$\text{RC (3, 1)}$]], |
| − | *$m = 3$: | + | *$m = 3$: $\text{(7, 4)}$ Hamming code, |
| − | *$m = 4$: | + | *$m = 4$: $\text{(15, 11)}$ Hamming code, |
| − | *$m = 5$: | + | *$m = 5$: $\text{(31, 26)}$ Hamming code, etc. |
| − | + | In the course of this exercise there are questions | |
| − | * | + | *to the code size $ |\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}|$, |
| − | * | + | *to the code rate $R$, and |
| − | * | + | *to the minimum distance $d_{\rm min}$. |
| − | + | Furthermore, we want to clarify whether the $\text{(7, 4)}$ Hamming code given for this task by its code table $\underline{u}_{i} ⇒ \underline{x}_{i}$ is systematic, and whether it is a so called "perfect code". The control index can take the values $i = 1, \text{...}\hspace{0.05cm} , 2^k =16$ . | |
| − | + | One speaks of a "perfect code" if the following condition is satisfied: | |
:$$2^k = \frac{2^n} {\sum_{f=0}^t {n \choose f}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$ | :$$2^k = \frac{2^n} {\sum_{f=0}^t {n \choose f}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$ | ||
| − | + | Here $t$ denotes the number of correctable errors. For odd minimum distance $d_{\rm min}$ holds: | |
:$$ t = \frac{d_{\rm min}-1 } {2} \hspace{0.05cm}.$$ | :$$ t = \frac{d_{\rm min}-1 } {2} \hspace{0.05cm}.$$ | ||
| − | + | The interpretation to this condition can be found in the sample solution. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | Hints: |
| + | *This exercise belongs to the chapter [[Channel_Coding/Examples_of_Binary_Block_Codes|"Examples of Binary Block Codes"]]. | ||
| + | |||
| + | *Reference is made to the section [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|"Hamming Codes"]]. | ||
| + | |||
| + | *For this Hamming code, different parity-check equations were used than in the [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|theory section]]. Therefore, the code tables also differ. | ||
| + | |||
| + | *In the [[Aufgaben:Exercise_1.07:_Check_and_Generator_Matrix_of_the_HC_(7,_4,_3)|Exercise 1.7]], where the same code is used, the chart of the parity-check equations is given. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Specify the characteristics of the given code $\mathcal{C}$: |
|type="{}"} | |type="{}"} | ||
| − | $ |\mathcal{C}| \ = \ $ { 16 } | + | $ |\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| \ = \ $ { 16 } |
| − | $ k \hspace{0. | + | $ k \hspace{0.46cm} = \ $ { 4 } |
| − | $ n \hspace{0. | + | $ n \hspace{0.44cm} = \ $ { 7 } |
| − | $ R\hspace{0. | + | $ R \hspace{0.40cm} = \ $ { 0.571 3% } |
| − | { | + | {Is this a systematic code? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - No. |
| − | { | + | {What is the minimum distance between any two code words? |
|type="{}"} | |type="{}"} | ||
$ \ d_{\rm min} \ = \ $ { 3 } | $ \ d_{\rm min} \ = \ $ { 3 } | ||
| − | { | + | {How many transmission errors can be detected $(e)$ or corrected $(t)$ respectively? |
|type="{}"} | |type="{}"} | ||
$e\hspace{0.22cm} = \ $ { 2 } | $e\hspace{0.22cm} = \ $ { 2 } | ||
$t\hspace{0.28cm} = \ $ { 1 } | $t\hspace{0.28cm} = \ $ { 1 } | ||
| − | { | + | {Is the Hamming code considered here "perfect"? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - No. |
| − | { | + | {Which statements are true regarding a "perfect code"? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - A perfect code always results in zero block error probability. |
| − | + | + | + All receive words $\underline{y}$ are assignable to a valid code word. |
| − | + | + | + For perfect codes, the minimum Hamming distance is odd. |
| − | { | + | {Which of the codes listed below are perfect? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The $\text{(15, 11)}$ Hamming code, |
| − | + | + | + the $\text{(63, 57)}$ Hamming code, |
| − | + | + | + the $\text{(3, 1)}$ repetition code, |
| − | - | + | - the $\text{(4, 1)}$ repetition Code, |
| − | + | + | + the $\text{(5, 1)}$ repetition code. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The code table has sixteen entries: $\underline{|C| = 16}$. |
| − | * | + | *From the equation $|C| = 2^k$ it follows that $\underline{k = 4}$. |
| − | * | + | *The length of each code word is $\underline{n = 7}$. |
| − | * | + | *Thus, the code rate is $\underline{R = 4/7} = 0.571$. |
| − | '''(2)''' | + | |
| − | * | + | '''(2)''' Correct <u>YES</u>: |
| + | *Each code word $\underline{x}$ first contains the $k = 4$ bits of the information word $\underline{u}$. This is followed by $m = 3$ check bits: | ||
:$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_5,x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3) \hspace{0.05cm}.$$ | :$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_5,x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3) \hspace{0.05cm}.$$ | ||
| − | * | + | *This corresponds exactly to the definition of a [[Channel_Coding/General_Description_of_Linear_Block_Codes|"systematic code"]] . |
| + | |||
| + | |||
| + | '''(3)''' For any Hamming code, the minimum distance $d_{\rm min} \underline{= 3}$. | ||
| + | *From the table, you can see that the minimum [[Channel_Coding/Objective_of_Channel_Coding#Some_Important_Definitions_of_Block_Coding|Hamming weight]] (the number of ones in a code word) is equal to 3. | ||
| + | *A linear code, in fact, also includes the zero word, so that holds: | ||
| + | :$$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} }\hspace{0.1cm}w_{\rm H}(\underline{x}) = 3 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' | + | '''(4)''' The specification $d_{\rm min} = 3$ means that $\underline{e = 2}$ errors can be detected and $\underline{t = 1}$ errors can be corrected. |
| − | '''(5)''' | + | |
| − | * | + | '''(5)''' Correct is <u>YES</u>: |
| + | *The condition for a perfect code is according to the specification: | ||
:$$ 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$ | :$$ 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$ | ||
| − | * | + | *In the $\text{(7, 4) Hamming code}$ considered here, $n = 7$, $m = 3$, and $t = 1$, giving a value of $8$ on both sides of the equation: |
:$$ 2^3 = 8\hspace{0.05cm}, \hspace{0.35cm} {\sum_{f=0}^1 {7 \choose f}} = {7 \choose 0} + {7 \choose 1} = 1 + 7 = 8 \hspace{0.05cm}.$$ | :$$ 2^3 = 8\hspace{0.05cm}, \hspace{0.35cm} {\sum_{f=0}^1 {7 \choose f}} = {7 \choose 0} + {7 \choose 1} = 1 + 7 = 8 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | [[File:P_ID2389__KC_A_1_6_ML.png| | + | '''(6)''' Correct <u>statements 2 and 3</u>: |
| + | *If there were a channel code with finite code word length $n$ that made the block error probability zero for all channels, it would not only be perfect, but a "miracle". | ||
| + | *But due to the channel coding theorem, ${\rm Pr(block error)} = 0$ is not even possible with finite $n$. | ||
| + | |||
| + | |||
| + | [[File:P_ID2389__KC_A_1_6_ML.png|right|frame|Illustration of a "perfect code"]] | ||
| − | + | Let's illustrate statement 2 with a graph. Here, the high-dimensional space is shown in a highly simplified way ("2D"). We assume the numerical values $k = 4$, $n = 7$, $m = 3$ and $t = 1$ of the $\text{(7, 4, 3)}$ Hamming code: | |
| − | * | + | *For the receive word, $2^7 = 128$ points are possible in seven-dimensional space. The red dots mark the $2^4 = 16$ valid code words. |
| − | * | + | *The circles include $8$ points each, namely a valid code word and $n = 7$ receive words after only one error, which are assigned to exactly this code word during decoding. |
| − | * | + | *Total there are $2^4 = 16$ such circles. Therefore, because of $128 = 16 \cdot 8$, not a single receive word $\underline{y}$ lies outside such an assignment circle. |
| − | + | Also the <u>last statement</u> is true, which shall be shown exemplarily for $d_{\rm min} = 4$: | |
| − | * | + | *Hereby also only $t = 1$ error can be corrected. |
| − | * | + | *If a receive word $\underline{y}$ differs from permissible code words in two bits, this point is not to be assigned to any circle. Then there are also points outside the circles and the condition of a "perfect code" is no longer fulfilled. |
| − | '''(7)''' | + | |
| − | * | + | '''(7)''' Correct are <u>statements 1, 2, 3 and 5</u>: |
| + | *All Hamming codes have the minimum Hamming distance $d_{\rm min} = 3$ ⇒ $t = 1$. | ||
| + | *At the same time, any $(n, k)$ Hamming code can also be written as a $(2^m - 1, 2^m - 1 - m)$ code, where $m = n - k$ indicates the number of parity bits. | ||
| + | *Thus, the equation of a "perfect code" is always satisfied: | ||
:$${\sum_{f=0}^1 {n \choose f}} = 1 + n = 2^m \hspace{0.05cm}.$$ | :$${\sum_{f=0}^1 {n \choose f}} = 1 + n = 2^m \hspace{0.05cm}.$$ | ||
| − | + | Where: | |
| − | *$m = 2$: | + | *$m = 2$: $\rm (3, 1)$ Hamming code, ⇒ identical to [[Channel_Coding/Examples_of_Binary_Block_Codes#RepetitionCodes|$\text{RC (3, 1)}$]], |
| − | *$m = 3$: (7, 4) | + | |
| − | *$m = 4$: (15, 11) | + | *$m = 3$: $\rm (7, 4)$ Hamming code, |
| − | *$m = 5$: (31, 26) | + | *$m = 4$: $\rm (15, 11)$ Hamming code, |
| − | *$m = 6$: (63, 57) | + | *$m = 5$: $\rm (31, 26)$ Hamming code, |
| + | *$m = 6$: $\rm (63, 57)$ Hamming code, | ||
| − | + | The repetition code with $n = 5$ also satisfies the condition. With $d_{\rm min} = 5$, $t = 2$ and $m = 4$ we obtain: | |
:$${\sum_{f=0}^2 {5 \choose f}} = 1 + 5 + 10 = 16 = 2^m \hspace{0.05cm}.$$ | :$${\sum_{f=0}^2 {5 \choose f}} = 1 + 5 + 10 = 16 = 2^m \hspace{0.05cm}.$$ | ||
| − | + | The other repetition codes $\rm (RC)$ with odd $n$ are also perfect, but not with even $n$: $\text{RC (4, 1)}$, $\text{RC (6, 1)}$, etc. This has already been justified in the solution to the subtask '''(6)'''. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^1.3 Examples of Binary Block Codes^]] |
| − | ^]] | ||
Latest revision as of 17:56, 1 November 2022
In 1962, Richard Wesley Hamming specified a class of binary block codes that differ in the number $m$ of check bits supplied. The code word length is always $n = 2^m - 1$. The information word consists of $k = n - m$ bits:
- $m = 2$: $\text{(3, 1)}$ Hamming code ⇒ identical to $\text{RC (3, 1)}$,
- $m = 3$: $\text{(7, 4)}$ Hamming code,
- $m = 4$: $\text{(15, 11)}$ Hamming code,
- $m = 5$: $\text{(31, 26)}$ Hamming code, etc.
In the course of this exercise there are questions
- to the code size $ |\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}|$,
- to the code rate $R$, and
- to the minimum distance $d_{\rm min}$.
Furthermore, we want to clarify whether the $\text{(7, 4)}$ Hamming code given for this task by its code table $\underline{u}_{i} ⇒ \underline{x}_{i}$ is systematic, and whether it is a so called "perfect code". The control index can take the values $i = 1, \text{...}\hspace{0.05cm} , 2^k =16$ .
One speaks of a "perfect code" if the following condition is satisfied:
- $$2^k = \frac{2^n} {\sum_{f=0}^t {n \choose f}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$
Here $t$ denotes the number of correctable errors. For odd minimum distance $d_{\rm min}$ holds:
- $$ t = \frac{d_{\rm min}-1 } {2} \hspace{0.05cm}.$$
The interpretation to this condition can be found in the sample solution.
Hints:
- This exercise belongs to the chapter "Examples of Binary Block Codes".
- Reference is made to the section "Hamming Codes".
- For this Hamming code, different parity-check equations were used than in the theory section. Therefore, the code tables also differ.
- In the Exercise 1.7, where the same code is used, the chart of the parity-check equations is given.
Questions
Solution
- From the equation $|C| = 2^k$ it follows that $\underline{k = 4}$.
- The length of each code word is $\underline{n = 7}$.
- Thus, the code rate is $\underline{R = 4/7} = 0.571$.
(2) Correct YES:
- Each code word $\underline{x}$ first contains the $k = 4$ bits of the information word $\underline{u}$. This is followed by $m = 3$ check bits:
- $$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_5,x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3) \hspace{0.05cm}.$$
- This corresponds exactly to the definition of a "systematic code" .
(3) For any Hamming code, the minimum distance $d_{\rm min} \underline{= 3}$.
- From the table, you can see that the minimum Hamming weight (the number of ones in a code word) is equal to 3.
- A linear code, in fact, also includes the zero word, so that holds:
- $$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}') = \min_{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} }\hspace{0.1cm}w_{\rm H}(\underline{x}) = 3 \hspace{0.05cm}.$$
(4) The specification $d_{\rm min} = 3$ means that $\underline{e = 2}$ errors can be detected and $\underline{t = 1}$ errors can be corrected.
(5) Correct is YES:
- The condition for a perfect code is according to the specification:
- $$ 2^m = {\sum_{f=0}^t {n \choose f}} \hspace{0.05cm}.$$
- In the $\text{(7, 4) Hamming code}$ considered here, $n = 7$, $m = 3$, and $t = 1$, giving a value of $8$ on both sides of the equation:
- $$ 2^3 = 8\hspace{0.05cm}, \hspace{0.35cm} {\sum_{f=0}^1 {7 \choose f}} = {7 \choose 0} + {7 \choose 1} = 1 + 7 = 8 \hspace{0.05cm}.$$
(6) Correct statements 2 and 3:
- If there were a channel code with finite code word length $n$ that made the block error probability zero for all channels, it would not only be perfect, but a "miracle".
- But due to the channel coding theorem, ${\rm Pr(block error)} = 0$ is not even possible with finite $n$.
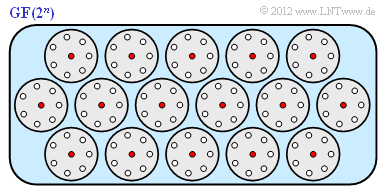
Let's illustrate statement 2 with a graph. Here, the high-dimensional space is shown in a highly simplified way ("2D"). We assume the numerical values $k = 4$, $n = 7$, $m = 3$ and $t = 1$ of the $\text{(7, 4, 3)}$ Hamming code:
- For the receive word, $2^7 = 128$ points are possible in seven-dimensional space. The red dots mark the $2^4 = 16$ valid code words.
- The circles include $8$ points each, namely a valid code word and $n = 7$ receive words after only one error, which are assigned to exactly this code word during decoding.
- Total there are $2^4 = 16$ such circles. Therefore, because of $128 = 16 \cdot 8$, not a single receive word $\underline{y}$ lies outside such an assignment circle.
Also the last statement is true, which shall be shown exemplarily for $d_{\rm min} = 4$:
- Hereby also only $t = 1$ error can be corrected.
- If a receive word $\underline{y}$ differs from permissible code words in two bits, this point is not to be assigned to any circle. Then there are also points outside the circles and the condition of a "perfect code" is no longer fulfilled.
(7) Correct are statements 1, 2, 3 and 5:
- All Hamming codes have the minimum Hamming distance $d_{\rm min} = 3$ ⇒ $t = 1$.
- At the same time, any $(n, k)$ Hamming code can also be written as a $(2^m - 1, 2^m - 1 - m)$ code, where $m = n - k$ indicates the number of parity bits.
- Thus, the equation of a "perfect code" is always satisfied:
- $${\sum_{f=0}^1 {n \choose f}} = 1 + n = 2^m \hspace{0.05cm}.$$
Where:
- $m = 2$: $\rm (3, 1)$ Hamming code, ⇒ identical to $\text{RC (3, 1)}$,
- $m = 3$: $\rm (7, 4)$ Hamming code,
- $m = 4$: $\rm (15, 11)$ Hamming code,
- $m = 5$: $\rm (31, 26)$ Hamming code,
- $m = 6$: $\rm (63, 57)$ Hamming code,
The repetition code with $n = 5$ also satisfies the condition. With $d_{\rm min} = 5$, $t = 2$ and $m = 4$ we obtain:
- $${\sum_{f=0}^2 {5 \choose f}} = 1 + 5 + 10 = 16 = 2^m \hspace{0.05cm}.$$
The other repetition codes $\rm (RC)$ with odd $n$ are also perfect, but not with even $n$: $\text{RC (4, 1)}$, $\text{RC (6, 1)}$, etc. This has already been justified in the solution to the subtask (6).