Difference between revisions of "Aufgaben:Exercise 1.2: ISDN and PCM"
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/General_Description_of_ISDN |
}} | }} | ||
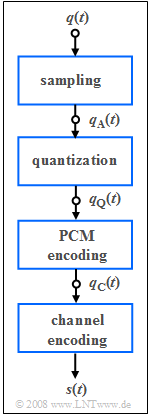
| − | [[File: | + | [[File:EN_Bei_A_1_2.png|right|frame|Components of PCM transmitter]] |
| − | + | The conversion of the analog speech signal $q(t)$ into the binary signal $q_{\rm C}(t)$ is done at $\rm ISDN$ ("Integrated Services Digital Network") according to the guidelines of "pulse code modulation" $\rm (PCM)$ by | |
| − | * | + | *sampling in the interval $T_{\rm A} = 1/f_{\rm A}$, |
| − | |||
| − | |||
| + | *quantization to $M = 256$ discrete values, | ||
| − | + | *binary PCM encoding with $N$ bits per quantization value. | |
| − | + | The net data rate of a $\rm B$ channel ("Bearer Channel") is $64 \ \rm kbit/s$ and corresponds to the bit rate of the redundancy-free binary signal $q_{\rm C}(t)$. | |
| + | |||
| + | However, because of the subsequent redundant channel coding and the inserted signaling bits, the gross data rate – i.e., the transmission rate of the transmitted signal $s(t)$ – is greater. | ||
| + | |||
| + | A measure for the quality of the entire ISDN transmission system is the sink SNR | ||
:$$\rho_{v} = \frac{P_q}{P_{\varepsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) - q(t)]^2}}$$ | :$$\rho_{v} = \frac{P_q}{P_{\varepsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) - q(t)]^2}}$$ | ||
| − | + | as the ratio of the powers | |
| + | *of the analog signal $q(t)$ bandlimited to the range $300 \ {\rm Hz}\ \text{...}\ 3400 \ {\rm Hz}$ | ||
| + | |||
| + | *and the error signal $\varepsilon (t) = v (t) - q(t)$. | ||
| + | |||
| + | An ideal signal reconstruction with an ideal rectangular low-pass filter is assumed here for the sink signal $v (t)$. | ||
| − | |||
| − | + | <u>Notes:</u> | |
| + | *The exercise refers to the chapter [[Examples_of_Communication_Systems/General_Description_of_ISDN|"General Description of ISDN"]] of this book. | ||
| + | *Reference is also made to the chapter [[Modulation_Methods/Pulse_Code_Modulation|"Pulse Code Modulation"]] of the book "Modulation Methods". | ||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {With how many bits $(N)$ is each quantized sample represented? |
|type="{}"} | |type="{}"} | ||
$N \ = \ $ { 8 3% } | $N \ = \ $ { 8 3% } | ||
| − | { | + | {What is the sampling rate $f_{\rm A} $? |
|type="{}"} | |type="{}"} | ||
$f_{\rm A} \ = \ $ { 8 3% } $ \ \rm kHz $ | $f_{\rm A} \ = \ $ { 8 3% } $ \ \rm kHz $ | ||
| − | { | + | {Does this satisfy the sampling theorem? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - no. |
| − | { | + | {Is the sink SNR $\rho_{v}$ at ISDN limited by the following effects? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Sampling (if sampling theorem is satisfied), |
| − | + | + | + AWGN noise (transmission error). |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The quantization level number $M$ is usually chosen as a power of two and for the number of bits $N = {\log_2}\hspace{0.05cm}(M)$. |
| + | *From $M = 2^{8} = 256$ follows $\underline{N = 8}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' For the bit rate, $R_{\rm B} = N \cdot f_{\rm A}$. | ||
| + | *Thus, from $R_{\rm B} = 64 \ \rm kbit/s$ and $N = 8$, we get $f_{\rm A} \hspace{0.15cm}\underline{= 8 \ \rm kHz}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Due to the bandwidth limitation, the highest frequency contained in the signal $q(t)$ is equal to $3.4 \ \rm kHz$. | ||
| + | |||
| + | *Therefore, according to the sampling theorem, $f_{\rm A} ≥ 6.8 \ \rm kHz$ should hold. | ||
| + | |||
| + | *With $f_{\rm A} = 8 \ \rm kHz$ the condition is fulfilled ⇒ $\underline {\rm YES}$. | ||
| − | |||
| − | '''( | + | '''(4)''' The <u>last statement</u> is correct: |
| + | *Even if the influence of the AWGN noise is small $($small noise power density $N_{0})$, the sink SNR $\rho_{v}$ cannot fall below a limit given by the quantization noise: | ||
| + | :$$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$ | ||
| − | + | *With larger noise interference, $\rho_{v}$ can further (significantly) be reduced by the transmission errors. | |
| − | |||
| − | + | *In contrast, sampling results in no loss of quality if the sampling theorem is obeyed. | |
| + | |||
| + | *Sampling can then be completely undone if the source signal $q(t)$ is bandlimited and the signal reconstruction is correctly dimensioned ⇒ ideal low-pass. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 70: | Line 96: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^1.1 General Description of ISDN^]] |
Latest revision as of 16:36, 23 January 2023
The conversion of the analog speech signal $q(t)$ into the binary signal $q_{\rm C}(t)$ is done at $\rm ISDN$ ("Integrated Services Digital Network") according to the guidelines of "pulse code modulation" $\rm (PCM)$ by
- sampling in the interval $T_{\rm A} = 1/f_{\rm A}$,
- quantization to $M = 256$ discrete values,
- binary PCM encoding with $N$ bits per quantization value.
The net data rate of a $\rm B$ channel ("Bearer Channel") is $64 \ \rm kbit/s$ and corresponds to the bit rate of the redundancy-free binary signal $q_{\rm C}(t)$.
However, because of the subsequent redundant channel coding and the inserted signaling bits, the gross data rate – i.e., the transmission rate of the transmitted signal $s(t)$ – is greater.
A measure for the quality of the entire ISDN transmission system is the sink SNR
- $$\rho_{v} = \frac{P_q}{P_{\varepsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) - q(t)]^2}}$$
as the ratio of the powers
- of the analog signal $q(t)$ bandlimited to the range $300 \ {\rm Hz}\ \text{...}\ 3400 \ {\rm Hz}$
- and the error signal $\varepsilon (t) = v (t) - q(t)$.
An ideal signal reconstruction with an ideal rectangular low-pass filter is assumed here for the sink signal $v (t)$.
Notes:
- The exercise refers to the chapter "General Description of ISDN" of this book.
- Reference is also made to the chapter "Pulse Code Modulation" of the book "Modulation Methods".
Questions
Solution
(1) The quantization level number $M$ is usually chosen as a power of two and for the number of bits $N = {\log_2}\hspace{0.05cm}(M)$.
- From $M = 2^{8} = 256$ follows $\underline{N = 8}$.
(2) For the bit rate, $R_{\rm B} = N \cdot f_{\rm A}$.
- Thus, from $R_{\rm B} = 64 \ \rm kbit/s$ and $N = 8$, we get $f_{\rm A} \hspace{0.15cm}\underline{= 8 \ \rm kHz}$.
(3) Due to the bandwidth limitation, the highest frequency contained in the signal $q(t)$ is equal to $3.4 \ \rm kHz$.
- Therefore, according to the sampling theorem, $f_{\rm A} ≥ 6.8 \ \rm kHz$ should hold.
- With $f_{\rm A} = 8 \ \rm kHz$ the condition is fulfilled ⇒ $\underline {\rm YES}$.
(4) The last statement is correct:
- Even if the influence of the AWGN noise is small $($small noise power density $N_{0})$, the sink SNR $\rho_{v}$ cannot fall below a limit given by the quantization noise:
- $$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$
- With larger noise interference, $\rho_{v}$ can further (significantly) be reduced by the transmission errors.
- In contrast, sampling results in no loss of quality if the sampling theorem is obeyed.
- Sampling can then be completely undone if the source signal $q(t)$ is bandlimited and the signal reconstruction is correctly dimensioned ⇒ ideal low-pass.