Difference between revisions of "Aufgaben:Exercise 1.3: Fictional University Somewhere"
m (Guenter verschob die Seite 1.3 Fiktive Uni Irgenwo nach Aufgabe 1.3: Fiktive Uni Irgenwo) |
|||
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Set_Theory_Basics |
}} | }} | ||
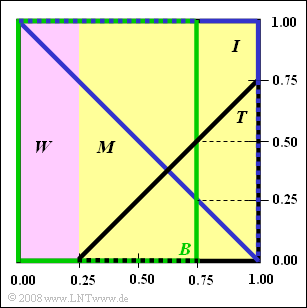
| − | [[File:P_ID89__Sto_A_1_3.png|right| | + | [[File:P_ID89__Sto_A_1_3.png|right|frame|Fictional University Somewhere]] |
| − | + | From the adjacent graph you can read some information about $\rm FUS$ ("Fictional University Somewhere"). The whole square represents the universal set $G$ of $960$ students. Of these | |
| − | *25% weiblich ( | + | *$25\%$ female (German: "weiblich") (set $W$, purple rectangle), |
| − | *75% männlich ( | + | *$75\%$ male (German: "männlich") (set $M$, yellow rectangle). |
| − | + | At the university there are the faculties of | |
| − | * | + | *Theology (set $T$,nbsp; black triangle), |
| − | * | + | *Information Technology (set $I$,nbsp; blue triangle), |
| − | * | + | *Business Administration (set $B$,nbsp; green rectangle). |
| − | |||
| − | + | Each student must be assigned to at least one of these faculties,nbsp; but can belong to two or three faculties at the same time. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Set_Theory_Basics|Set Theory Basics]]. | ||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video | ||
| + | :[[Mengentheoretische_Begriffe_und_Gesetzmäßigkeiten_(Lernvideo)|Mengentheoretische Begriffe und Gesetzmäßigkeiten]] $\Rightarrow$ "Set Theoretical Concepts and Laws". | ||
| + | *The areas in the above diagram are to scale, so you can easily give the (percentage) occupancy figures using the numerical values given and simple geometric considerations. | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the number of students enrolled in the faculties. As a check, enter the number of students in the Faculty of Theology $(N_{\rm T})$. |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm T} \ =$ { 270 3% } | + | $N_{\rm T} \ = \ $ { 270 3% } |
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - $I$ | + | - $I$ is a subset of $M$. |
| − | + $W$ | + | + $W$ is a subset of $B$. |
| − | + $W$ | + | + $W$ and $M$ together form a "complete system". |
| − | - $B$, $I$ | + | - $B$, $I$ and $T$ together form a "complete system". |
| − | + $W$ | + | + $W$ and $T$ are disjoint sets. |
| − | + | + | + The union of $B$, $I$ and $T$ gives the universal set $G$. |
| − | - | + | - The intersection of $B$, $I$ and $T$ gives the empty set $\phi$. |
| − | { | + | {What is the proportion of female IT students relative to all students? |
|type="{}"} | |type="{}"} | ||
| − | $\text{Pr[IT | + | $\text{Pr}\big[\text{female IT student}\big] \ = \ $ { 3.13 3% } $\ \%$ |
| − | { | + | {What is the proportion of students with only one field of study? |
|type="{}"} | |type="{}"} | ||
| − | $\text{Pr[ | + | $\text{Pr}\big[\text{one field of study}\big] \ = \ $ { 48.43 3% } $\ \%$ |
| − | { | + | {What is the percentage of students with three fields of study? |
|type="{}"} | |type="{}"} | ||
| − | $\text{Pr[ | + | $\text{Pr}\big[\text{three fields of study}\big] \ = \ $ { 1.56 3% } $\ \%$ |
| − | { | + | {What is the percentage of students with two fields of study? |
|type="{}"} | |type="{}"} | ||
| − | $\text{Pr[ | + | $\text{Pr}\big[\text{two fields of study}\big] \ = \ $ { 50 3% } $\ \%$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From simple geometric considerations, we arrive at the results: |
| + | |||
| + | :$${\rm Pr}(B) = 3/4 \cdot 1 = 3/4\hspace{0.3cm}(\text{absolute:}\ 720),$$ | ||
| + | |||
| + | :$${\rm Pr}(I) = {1}/{2}\cdot 1\cdot 1 = 1/2\hspace{0.3cm}(\text{absolute:} \ 480),$$ | ||
| + | |||
| + | :$${\rm Pr}(T) = {1}/{2} \cdot {3}/{4} \cdot {3}/{4} = {9}/{32} \hspace{0.3cm}(\text{absolute:}\ 270)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm T} \;\underline{= 270}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' <u>Proposed solutions 2, 3, 5 and 6</u> are correct ⇒ proposed solutions 1, 4, 7 are consequently incorrect: | ||
| + | *There are also female IT students, although very few. | ||
| + | *The union of $B$, $I$ and $T$ gives the universal set, but not a complete system (not all combinations of $B$, $I$ and $T$ are disjoint). | ||
| + | *For the same reason, the intersection of $B$, $I$ and $T$ does not yield the empty set. | ||
| + | |||
| + | |||
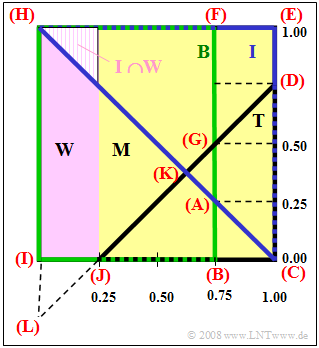
| + | [[File:P_ID181__Sto_A_1_3_d_neu.png|right|frame|Geometric solution of a probability problem]] | ||
| + | '''(3)''' In set theory, an IT student is the intersection of $I$ and $W$ <br>(shown as a shaded area in the upper left of the graph): | ||
| − | $${ | + | :$$\text{Pr[female IT student] = Pr}(I \cap W) = {1}/{2}\cdot {1}/{4} \cdot {1}/{4} = {1}/{32} \hspace{0.15cm}\underline { \thickapprox 3.13 \%}.$$ |
| − | $$ | + | In words, there are $30$ female IT students among the $960$ students. |
| − | |||
| − | '''( | + | '''(4)''' The probability can be calculated as the sum of three individual probabilities: |
| − | + | :$$ \text{Pr[one field of study] = Pr}( \overline{B} \cap \overline{I} \cap T) + {\rm Pr}( \overline{B} \cap I \cap \overline{T}) + {\rm Pr}( \it B \cap \overline{I} \cap \overline{T}).$$ | |
| − | |||
| − | |||
| + | *Each individual probability corresponds to an area in the Venn diagram and can be determined by addition or subtraction of triangles or rectangles (see graph): | ||
| + | :$$p_1 = {\rm Pr}( \overline{B} \cap \overline{I} \cap T) = {\rm Triangle\ (ABC)}= \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm}\frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm}\frac{1}{4}= \frac{1}{32}\hspace{0.1cm}\underline{\approx 0.0313},$$ | ||
| + | :$$p_2 ={\rm Pr}( \overline{B} \cap I \cap \overline{T}) = {\rm Rectangle\hspace{0.1cm}(DEFG)}= \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}+ \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4} = \frac{3}{32}\hspace{0.1cm}\underline{\approx 0.0938},$$ | ||
| − | + | :$$p_3 = {\rm Triangle\hspace{0.1cm}(HIC)}- {\rm Triangle\hspace{0.1cm}(KJC)} ={1}/{2}\hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} - \hspace{0.1cm}{1}/{2}\hspace{0.05cm} \cdot \hspace{0.1cm} {3}/{4} \cdot {3}/{8} = {23}/{64}.$$ | |
| − | |||
| − | + | $\text{Or:}\hspace{0.3cm}$ | |
| − | + | :$$p_3 = {\rm Pr}( B \cap \overline{I} \cap \overline{T}) ={\rm Rectangle\hspace{0.1cm}(HIJK)}= {\rm Triangle\hspace{0.1cm}(HLK)}- {\rm Triangle\hspace{0.1cm}(ILJ)} = \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{4}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{8}\hspace{0.02cm} - \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{1}{4} \cdot \frac{1}{4} = \frac{23}{64}\hspace{0.1cm}\underline{\approx 0.3594}.$$ | |
| + | *The sum of these three probabilities leads to the final result $ \text{Pr[one field of study] } = 31/64 \;\underline {\approx 48.43 \%}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(5)''' This probability is expressed by the triangle $\text{Triangle(AGK)}$ . This has the area | |
| + | :$$\text{Pr[three fields of study]} = {1}/{2}\cdot {1}/{4}\cdot {1}/{8} = {1}/{64}\hspace{0.15cm}\underline{\approx 1.56 \%}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(6)''' The three events |
| − | + | * "only one field of study", | |
| + | *"two fields of study" and | ||
| + | *"three fields of study" | ||
| − | + | form a complete system. Thus, using the results of the last subtasks, we obtain: | |
| − | + | :$$\text{Pr[two fields of study]} = 1- \text{Pr[one field of study] } - \text{[three fields of study]}= 1- {31}/{64} - {1}/{64} \hspace{0.15cm}\underline{= 50\%}.$$ | |
| − | $$\ | + | One would arrive at exactly the same result – but with considerably more effort – in the direct way accordingly: |
| − | + | :$$\text{Pr[two fields of study]} = {\rm Pr}(B\cap I \cap\overline{T}) + {\rm Pr}(B\cap\overline{I}\cap{T}) + {\rm Pr}(\overline{B}\cap I \cap T).$$ | |
| − | $$\ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.2 Set Theory Basics^]] |
Latest revision as of 15:09, 25 November 2021
From the adjacent graph you can read some information about $\rm FUS$ ("Fictional University Somewhere"). The whole square represents the universal set $G$ of $960$ students. Of these
- $25\%$ female (German: "weiblich") (set $W$, purple rectangle),
- $75\%$ male (German: "männlich") (set $M$, yellow rectangle).
At the university there are the faculties of
- Theology (set $T$,nbsp; black triangle),
- Information Technology (set $I$,nbsp; blue triangle),
- Business Administration (set $B$,nbsp; green rectangle).
Each student must be assigned to at least one of these faculties,nbsp; but can belong to two or three faculties at the same time.
Hints:
- The exercise belongs to the chapter Set Theory Basics.
- The topic of this chapter is illustrated with examples in the (German language) learning video
- Mengentheoretische Begriffe und Gesetzmäßigkeiten $\Rightarrow$ "Set Theoretical Concepts and Laws".
- The areas in the above diagram are to scale, so you can easily give the (percentage) occupancy figures using the numerical values given and simple geometric considerations.
Questions
Solution
(1) From simple geometric considerations, we arrive at the results:
- $${\rm Pr}(B) = 3/4 \cdot 1 = 3/4\hspace{0.3cm}(\text{absolute:}\ 720),$$
- $${\rm Pr}(I) = {1}/{2}\cdot 1\cdot 1 = 1/2\hspace{0.3cm}(\text{absolute:} \ 480),$$
- $${\rm Pr}(T) = {1}/{2} \cdot {3}/{4} \cdot {3}/{4} = {9}/{32} \hspace{0.3cm}(\text{absolute:}\ 270)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm T} \;\underline{= 270}.$$
(2) Proposed solutions 2, 3, 5 and 6 are correct ⇒ proposed solutions 1, 4, 7 are consequently incorrect:
- There are also female IT students, although very few.
- The union of $B$, $I$ and $T$ gives the universal set, but not a complete system (not all combinations of $B$, $I$ and $T$ are disjoint).
- For the same reason, the intersection of $B$, $I$ and $T$ does not yield the empty set.
(3) In set theory, an IT student is the intersection of $I$ and $W$
(shown as a shaded area in the upper left of the graph):
- $$\text{Pr[female IT student] = Pr}(I \cap W) = {1}/{2}\cdot {1}/{4} \cdot {1}/{4} = {1}/{32} \hspace{0.15cm}\underline { \thickapprox 3.13 \%}.$$
In words, there are $30$ female IT students among the $960$ students.
(4) The probability can be calculated as the sum of three individual probabilities:
- $$ \text{Pr[one field of study] = Pr}( \overline{B} \cap \overline{I} \cap T) + {\rm Pr}( \overline{B} \cap I \cap \overline{T}) + {\rm Pr}( \it B \cap \overline{I} \cap \overline{T}).$$
- Each individual probability corresponds to an area in the Venn diagram and can be determined by addition or subtraction of triangles or rectangles (see graph):
- $$p_1 = {\rm Pr}( \overline{B} \cap \overline{I} \cap T) = {\rm Triangle\ (ABC)}= \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm}\frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm}\frac{1}{4}= \frac{1}{32}\hspace{0.1cm}\underline{\approx 0.0313},$$
- $$p_2 ={\rm Pr}( \overline{B} \cap I \cap \overline{T}) = {\rm Rectangle\hspace{0.1cm}(DEFG)}= \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}+ \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4} = \frac{3}{32}\hspace{0.1cm}\underline{\approx 0.0938},$$
- $$p_3 = {\rm Triangle\hspace{0.1cm}(HIC)}- {\rm Triangle\hspace{0.1cm}(KJC)} ={1}/{2}\hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} - \hspace{0.1cm}{1}/{2}\hspace{0.05cm} \cdot \hspace{0.1cm} {3}/{4} \cdot {3}/{8} = {23}/{64}.$$
$\text{Or:}\hspace{0.3cm}$
- $$p_3 = {\rm Pr}( B \cap \overline{I} \cap \overline{T}) ={\rm Rectangle\hspace{0.1cm}(HIJK)}= {\rm Triangle\hspace{0.1cm}(HLK)}- {\rm Triangle\hspace{0.1cm}(ILJ)} = \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{4}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{8}\hspace{0.02cm} - \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{1}{4} \cdot \frac{1}{4} = \frac{23}{64}\hspace{0.1cm}\underline{\approx 0.3594}.$$
- The sum of these three probabilities leads to the final result $ \text{Pr[one field of study] } = 31/64 \;\underline {\approx 48.43 \%}$.
(5) This probability is expressed by the triangle $\text{Triangle(AGK)}$ . This has the area
- $$\text{Pr[three fields of study]} = {1}/{2}\cdot {1}/{4}\cdot {1}/{8} = {1}/{64}\hspace{0.15cm}\underline{\approx 1.56 \%}.$$
(6) The three events
- "only one field of study",
- "two fields of study" and
- "three fields of study"
form a complete system. Thus, using the results of the last subtasks, we obtain:
- $$\text{Pr[two fields of study]} = 1- \text{Pr[one field of study] } - \text{[three fields of study]}= 1- {31}/{64} - {1}/{64} \hspace{0.15cm}\underline{= 50\%}.$$
One would arrive at exactly the same result – but with considerably more effort – in the direct way accordingly:
- $$\text{Pr[two fields of study]} = {\rm Pr}(B\cap I \cap\overline{T}) + {\rm Pr}(B\cap\overline{I}\cap{T}) + {\rm Pr}(\overline{B}\cap I \cap T).$$