Difference between revisions of "Aufgaben:Exercise 1.5: Binary Markov Source"
m (Guenter verschob die Seite 1.5 Binäre Markovquelle nach Aufgabe 1.5: Binäre Markovquelle) |
|||
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Discrete_Sources_with_Memory |
}} | }} | ||
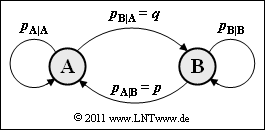
| − | [[File:P_ID2250__Inf_A_1_5.png|right| | + | [[File:P_ID2250__Inf_A_1_5.png|right|frame|Binary Markov diagram]] |
| − | + | [[Aufgaben:Exercise_1.4:_Entropy_Approximations_for_the_AMI_Code|Exercise 1.4]] has shown that the calculation of the entropy for a source with memory can be very time-consuming. One must then first calculate (very many) entropy approximations $H_k$ for $k$–tuples and only then the source entropy can be determined with the boundary transition $k \to \infty$ : | |
:$$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$ | :$$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$ | ||
| − | + | Often, $H_k$ tends only very slowly towards the limit $H$. | |
| − | + | The calculation process is drastically reduced if the message source has Markov properties. The graphic shows the transition diagram for a binary Markov source with the two states (symbols) $\rm A$ and $\rm B$. | |
| − | |||
| − | |||
| + | *This is clearly determined by the two conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q$ . | ||
| + | *The other conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}$ as well as the (unconditional) symbol probabilities $p_{\rm A}$ and $p_{\rm B}$ can be determined from this. | ||
| − | + | ||
| + | The entropy of the binary Markov chain (with the unit "bit/symbol") is then: | ||
:$$H = H_{\rm M} = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot | :$$H = H_{\rm M} = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot | ||
{\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | It should be noted that in the argument of the "binary logarithm", the [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability|conditional probabilities]] $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$, $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$, ... are to be used, while the [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability|"Conditional Probabilities"]] $p_{\rm AA}$, $p_{\rm AB}$, ... are to be used for the weighting. | |
| − | + | Using the first order entropy approximation, | |
:$$H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A}} + p_{\rm B} \cdot | :$$H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A}} + p_{\rm B} \cdot | ||
{\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} | {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} | ||
| − | \hspace{0.5cm}({\rm | + | \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol})\hspace{0.05cm},$$ |
| − | + | as well as the (actual) entropy $H = H_{\rm M}$ given above, all further entropy approximations $(k = 2, 3, \text{...})$ can also be given directly for a Markov source: | |
| − | :$$H_k = \frac{1}{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] | + | :$$H_k = \frac{1}{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M} \big ] |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '' | + | |
| − | * | + | |
| − | * | + | ''Hints:'' |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Discrete_Sources_with_Memory|Discrete Sources with Memory]]. |
| − | * | + | *Reference is also made in particular to the two pages [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Intersection|"Intersection"]] and [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability|"Conditional Probability"]]. |
| − | + | *With the exception of subtask '''(6)''' $p = 1/4$ and $q = 1/2$ always apply. | |
| + | |||
| + | *For the (ergodic) symbol probabilities of a first order Markov chain applies: | ||
:$$ p_{\rm A} = \frac {p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} | :$$ p_{\rm A} = \frac {p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} | ||
{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.3cm} | { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.3cm} | ||
| Line 40: | Line 43: | ||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Give the transition probabilities for $p = 1/4$ and $q = 1/2$. |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \ = $ { 0.5 3% } | + | $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \ = \ $ { 0.5 3% } |
| − | $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \ = $ { 0.75 3% } | + | $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \ = \ $ { 0.75 3% } |
| − | { | + | {What are the (unconditional) symbol probabilities? Let $p = 1/4$ and $q = 1/2$ still hold. |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm A} \ = $ { 0.333 3% } | + | $p_{\rm A} \ = \ $ { 0.333 3% } |
| − | $p_{\rm B} \ = ${ 0.667 3% } | + | $p_{\rm B} \ = \ ${ 0.667 3% } |
| − | { | + | {Give the corresponding first order entropy approximation. |
|type="{}"} | |type="{}"} | ||
| − | $H_1 \ = $ { 0.918 1% } $\ \rm bit/ | + | $H_1 \ = \ $ { 0.918 1% } $\ \rm bit/symbol$ |
| − | { | + | {What is the entropy $H = H_{\rm M}$ of this Markov source with $p = 1/4$ and $q = 1/2$? |
|type="{}"} | |type="{}"} | ||
| − | $H \ =$ { 0.875 1% } $\ \rm bit/ | + | $H \ = \ $ { 0.875 1% } $\ \rm bit/symbol$ |
| − | { | + | {Which entropy approximations $H_k$ result from the Markov properties? |
|type="{}"} | |type="{}"} | ||
| − | $H_2 \ =$ { 0.897 0.5% } $\ \rm bit/ | + | $H_2 \ = \ $ { 0.897 0.5% } $\ \rm bit/symbol$ |
| − | $H_3 \ =$ { 0.889 0.5% } $\ \rm bit/ | + | $H_3 \ = \ $ { 0.889 0.5% } $\ \rm bit/symbol$ |
| − | $H_4 \ =$ { 0.886 0.5% } $\ \rm bit/ | + | $H_4 \ = \ $ { 0.886 0.5% } $\ \rm bit/symbol$ |
| − | { | + | {What is the entropy $H = H_{\rm M}$ of the Markov source with $p = 1/4$ and $q = 3/4$? |
|type="{}"} | |type="{}"} | ||
| − | $H \ =$ { 0.811 1% } $\ \rm bit/ | + | $H \ = \ $ { 0.811 1% } $\ \rm bit/symbol$ |
| Line 80: | Line 85: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
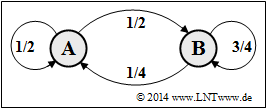
| − | [[File:Inf_A_1_5a_vers2.png|right| | + | [[File:Inf_A_1_5a_vers2.png|right|frame|Markov diagram for tasks '''(1)''', ... , '''(5)''']] |
| − | + | After $\rm A$ , $\rm A$ and $\rm B$ are equally probable. After $\rm B$ , $\rm B$ occurs much more frequently than $\rm A$ . The following applies to the transition probabilities | |
:$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}= 1 - q \hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm},$$ | :$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}= 1 - q \hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm},$$ | ||
:$$ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}= 1 - p \hspace{0.15cm} \underline {= 0.75} \hspace{0.05cm}.$$ | :$$ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}= 1 - p \hspace{0.15cm} \underline {= 0.75} \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | |
| + | |||
| + | '''(2)''' According to the equations given: | ||
:$$p_{\rm A}= \frac{p}{p+q} = \frac{0.25}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.333} \hspace{0.05cm}, \hspace{0.5cm} | :$$p_{\rm A}= \frac{p}{p+q} = \frac{0.25}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.333} \hspace{0.05cm}, \hspace{0.5cm} | ||
p_{\rm B} = \frac{q}{p+q} = \frac{0.50}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.667} \hspace{0.05cm}.$$ | p_{\rm B} = \frac{q}{p+q} = \frac{0.50}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.667} \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| + | |||
| + | '''(3)''' With the probabilities calculated in the last sub-task: | ||
:$$H_{\rm 1} = H_{\rm bin}(p_{\rm A}) = 1/3 \cdot {\rm log}_2\hspace{0.01cm} (3) + 2/3 \cdot {\rm log}_2\hspace{0.01cm} (1.5) = | :$$H_{\rm 1} = H_{\rm bin}(p_{\rm A}) = 1/3 \cdot {\rm log}_2\hspace{0.01cm} (3) + 2/3 \cdot {\rm log}_2\hspace{0.01cm} (1.5) = | ||
| − | 1.585 - 2/3\hspace{0.15cm} \underline {= 0.918 \,{\rm bit/ | + | 1.585 - 2/3\hspace{0.15cm} \underline {= 0.918 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| + | |||
| + | '''(4)''' The entropy of the Markov source is according to: | ||
:$$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot | :$$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot | ||
{\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *For the composite probabilities holds: | |
:$$p_{\rm AA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = (1-q) \cdot \frac{p}{p+q} = | :$$p_{\rm AA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = (1-q) \cdot \frac{p}{p+q} = | ||
\frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$ | \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$ | ||
| Line 111: | Line 122: | ||
:$$\Rightarrow\hspace{0.3cm} H = 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot | :$$\Rightarrow\hspace{0.3cm} H = 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot | ||
{\rm log}_2\hspace{0.01cm} (4) + 1/2 \cdot {\rm log}_2\hspace{0.1cm} (4/3) = | {\rm log}_2\hspace{0.01cm} (4) + 1/2 \cdot {\rm log}_2\hspace{0.1cm} (4/3) = | ||
| − | 10/6 - 1/2 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.875 \,{\rm bit/ | + | 10/6 - 1/2 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.875 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | |
| − | :$$H_2 = {1}/{2} \cdot [ 0.918 + 1 \cdot 0.875] \hspace{0.15cm} \underline {= 0.897 \,{\rm bit/ | + | |
| + | '''(5)''' In general, with $H_{\rm M} = H$ for $k$–th entropy approximation: | ||
| + | :$$H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] \hspace{0.05cm}.$$ | ||
| + | *It follows that: | ||
| + | :$$H_2 = {1}/{2} \cdot [ 0.918 + 1 \cdot 0.875] \hspace{0.15cm} \underline {= 0.897 \,{\rm bit/symbol}} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | :$$ H_3 = {1}/{3} \cdot [ 0.918 + 2 \cdot 0.875] \hspace{0.15cm} \underline {= 0.889 \,{\rm bit/ | + | :$$ H_3 = {1}/{3} \cdot [ 0.918 + 2 \cdot 0.875] \hspace{0.15cm} \underline {= 0.889 \,{\rm bit/symbol}} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | :$$ H_4 = {1}/{4} \cdot [ 0.918 + 3 \cdot 0.875] \hspace{0.15cm} \underline {= 0.886 \,{\rm bit/ | + | :$$ H_4 = {1}/{4} \cdot [ 0.918 + 3 \cdot 0.875] \hspace{0.15cm} \underline {= 0.886 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | [[File:Inf_A_1_5f_vers2.png|right| | + | |
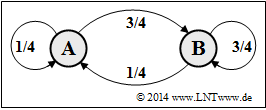
| − | '''(6)''' | + | [[File:Inf_A_1_5f_vers2.png|right|frame|Markov diagram for subtask '''(6)''']] |
| + | '''(6)''' With the new set of parameters $(p = 1/4, q = 3/4)$, we obtain for the symbol probabilities: | ||
| + | :$$ p_{\rm A} = 1/4, \ p_{\rm B} = 3/4.$$ | ||
| + | |||
| + | *This special case thus leads to statistically independent symbols: | ||
:$$ p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} | :$$ p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} | ||
\hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} | \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Thus the entropy $H$ is identical with the entropy approximation $H_1$: | |
:$$H = H_{\rm 1} = 1/4 \cdot {\rm log}_2\hspace{0.01cm} (4) + 3/4 \cdot {\rm log}_2\hspace{0.01cm} (4/3) = | :$$H = H_{\rm 1} = 1/4 \cdot {\rm log}_2\hspace{0.01cm} (4) + 3/4 \cdot {\rm log}_2\hspace{0.01cm} (4/3) = | ||
2 - 0.75 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Symbol}} | 2 - 0.75 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Symbol}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *The entropy approximations $H_2$, $H_3$, $H_4$, ... also yield the result $0.811 \, \rm bit/symbol$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.2 Sources with Memory^]] |
Latest revision as of 13:03, 10 August 2021
Exercise 1.4 has shown that the calculation of the entropy for a source with memory can be very time-consuming. One must then first calculate (very many) entropy approximations $H_k$ for $k$–tuples and only then the source entropy can be determined with the boundary transition $k \to \infty$ :
- $$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$
Often, $H_k$ tends only very slowly towards the limit $H$.
The calculation process is drastically reduced if the message source has Markov properties. The graphic shows the transition diagram for a binary Markov source with the two states (symbols) $\rm A$ and $\rm B$.
- This is clearly determined by the two conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q$ .
- The other conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}$ as well as the (unconditional) symbol probabilities $p_{\rm A}$ and $p_{\rm B}$ can be determined from this.
The entropy of the binary Markov chain (with the unit "bit/symbol") is then:
- $$H = H_{\rm M} = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
It should be noted that in the argument of the "binary logarithm", the conditional probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}$, $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$, ... are to be used, while the "Conditional Probabilities" $p_{\rm AA}$, $p_{\rm AB}$, ... are to be used for the weighting.
Using the first order entropy approximation,
- $$H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol})\hspace{0.05cm},$$
as well as the (actual) entropy $H = H_{\rm M}$ given above, all further entropy approximations $(k = 2, 3, \text{...})$ can also be given directly for a Markov source:
- $$H_k = \frac{1}{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M} \big ] \hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter Discrete Sources with Memory.
- Reference is also made in particular to the two pages "Intersection" and "Conditional Probability".
- With the exception of subtask (6) $p = 1/4$ and $q = 1/2$ always apply.
- For the (ergodic) symbol probabilities of a first order Markov chain applies:
- $$ p_{\rm A} = \frac {p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.3cm} p_{\rm B} = \frac {p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$
Questions
Solution
After $\rm A$ , $\rm A$ and $\rm B$ are equally probable. After $\rm B$ , $\rm B$ occurs much more frequently than $\rm A$ . The following applies to the transition probabilities
- $$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}= 1 - q \hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm},$$
- $$ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}= 1 - p \hspace{0.15cm} \underline {= 0.75} \hspace{0.05cm}.$$
(2) According to the equations given:
- $$p_{\rm A}= \frac{p}{p+q} = \frac{0.25}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.333} \hspace{0.05cm}, \hspace{0.5cm} p_{\rm B} = \frac{q}{p+q} = \frac{0.50}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.667} \hspace{0.05cm}.$$
(3) With the probabilities calculated in the last sub-task:
- $$H_{\rm 1} = H_{\rm bin}(p_{\rm A}) = 1/3 \cdot {\rm log}_2\hspace{0.01cm} (3) + 2/3 \cdot {\rm log}_2\hspace{0.01cm} (1.5) = 1.585 - 2/3\hspace{0.15cm} \underline {= 0.918 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(4) The entropy of the Markov source is according to:
- $$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
- For the composite probabilities holds:
- $$p_{\rm AA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = (1-q) \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$
- $$ p_{\rm AB} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = q \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = {1}/{6} \hspace{0.05cm},$$
- $$ p_{\rm BA} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = p \cdot \frac{q}{p+q} = p_{\rm AB} = {1}/{6} \hspace{0.05cm},$$
- $$ p_{\rm BB} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-p) \cdot \frac{q}{p+q} = \frac{3/4 \cdot 1/2}{3/4} = {1}/{2} $$
- $$\Rightarrow\hspace{0.3cm} H = 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (4) + 1/2 \cdot {\rm log}_2\hspace{0.1cm} (4/3) = 10/6 - 1/2 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.875 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(5) In general, with $H_{\rm M} = H$ for $k$–th entropy approximation:
- $$H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] \hspace{0.05cm}.$$
- It follows that:
- $$H_2 = {1}/{2} \cdot [ 0.918 + 1 \cdot 0.875] \hspace{0.15cm} \underline {= 0.897 \,{\rm bit/symbol}} \hspace{0.05cm},$$
- $$ H_3 = {1}/{3} \cdot [ 0.918 + 2 \cdot 0.875] \hspace{0.15cm} \underline {= 0.889 \,{\rm bit/symbol}} \hspace{0.05cm},$$
- $$ H_4 = {1}/{4} \cdot [ 0.918 + 3 \cdot 0.875] \hspace{0.15cm} \underline {= 0.886 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(6) With the new set of parameters $(p = 1/4, q = 3/4)$, we obtain for the symbol probabilities:
- $$ p_{\rm A} = 1/4, \ p_{\rm B} = 3/4.$$
- This special case thus leads to statistically independent symbols:
- $$ p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}.$$
- Thus the entropy $H$ is identical with the entropy approximation $H_1$:
- $$H = H_{\rm 1} = 1/4 \cdot {\rm log}_2\hspace{0.01cm} (4) + 3/4 \cdot {\rm log}_2\hspace{0.01cm} (4/3) = 2 - 0.75 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
- The entropy approximations $H_2$, $H_3$, $H_4$, ... also yield the result $0.811 \, \rm bit/symbol$.