Difference between revisions of "Aufgaben:Exercise 3.13: Code Rate and Reliability"
m (Guenter verschob die Seite 3.13 Coderate und Zuverlässigkeit nach Aufgabe 3.13: Coderate und Zuverlässigkeit) |
|||
| (21 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Application_to_Digital_Signal_Transmission |
}} | }} | ||
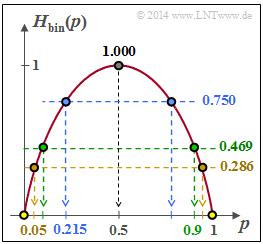
| − | [[File:P_ID2805__Inf_A_3_12.png|right|frame| | + | [[File:P_ID2805__Inf_A_3_12.png|right|frame|Binary entropy function]] |
| − | + | [https://en.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon's] channel coding theorem states, among other things, that a channel can be used to transmit with an arbitrarily small block error probability as long as the code rate $R$ is not greater than the channel capacity $C$. However, this result can only be achieved with channel coding for very large block lengths: $n → ∞$, which is associated with an arbitrarily large effort. | |
| − | + | This statement is based on information-theoretical laws that Shannon himself established. However, Shannon does not say what this "infinitely good" channel coding must look like, he only proves that it exists. | |
| − | + | The inverse of the channel coding theorem states that no error-free transmission is possible with a rate $R > C$. There is then no coding system with a vanishingly small error probability, no matter how elaborate and sophisticated the coding. | |
| − | |||
| − | * | + | Rather, two bounds can be specified for the case $R > C$ : |
| − | :$$ p_{\rm B} \ge H_{\rm bin}^{-1} \left (1 - | + | |
| − | * | + | *If one transmits via a "discrete memoryless channel" $\rm (DMC)$ with a rate $R$ greater than the channel capacity $C$, there is a lower bound for the bit error probability: |
| + | :$$ p_{\rm B} \ge H_{\rm bin}^{-1} \left (1 - {C}/{R} \right) > 0 \hspace{0.05cm}.$$ | ||
| + | *If the bit error probability is not to exceed the value $p_{\rm B}$ after best possible decoding, the rate must not exceed a certain limit: | ||
:$$ R \le \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.05cm}.$$ | :$$ R \le \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.05cm}.$$ | ||
| − | In | + | In this exercise, these equations are to be evaluated numerically using the [[Information_Theory/Ged%C3%A4chtnislose_Nachrichtenquellen#Binary_entropy_function|binary entropy function]] |
| − | :$$ H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$ | + | :$$ H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}.$$ |
| − | + | $H_{\rm bin}(p)$ is sketched above. Because of $0 < p_B ≤ 1$ and $0 < C/R < 1$ the argument of the function $H_{\rm bin}(⋅)$ and its inverse $H_{\rm bin}^{ –1 }(⋅)$ is always between $0$ and $1$. | |
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | Hints: |
| + | *The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to digital signal transmission]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Rate.2C_channel_capacity_and_bit_error_probability|Rate, channel capacity and bit error probability]]. | ||
| + | *The values of the binary entropy function are provided, for example, by the (German language) interactive SWF applet<br> [[Applets:Entropien_von_Nachrichtenquellen|Entropien und Näherungen von digitalen Nachrichtenquellen]] ⇒ "Entropies and approximations of digital sources". | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the lower bit error probability bound for $\underline{R/C = 4}$? |
|type="{}"} | |type="{}"} | ||
$p_{\text{B, min}} \ = \ $ { 0.215 3% } | $p_{\text{B, min}} \ = \ $ { 0.215 3% } | ||
| − | { | + | {At what rate $R$ you can transmit over a channel with capacity $\underline{C = 0.5 \ \rm (bit)}$ for a given marginal error probability $p_{\rm B}$ ? |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm B} = 0.10\text{:} \ | + | $p_{\rm B} = 0.10\text{:} \hspace{0.5cm}R_{\rm max} \ = \ $ { 0.942 3% } |
| − | $p_{\rm B} = 0.05\text{:} \ | + | $p_{\rm B} = 0.05\text{:} \hspace{0.5cm}R_{\rm max} \ = \ $ { 0.7 3% } |
| − | { | + | {What is the relation between $H_{\rm bin}(p)$ and the approximation $p · \log_2 (1/p)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $H_{\rm bin}(p) < p · \log_2 \, (1/p)$ is valid. |
| − | + | + | + $H_{\rm bin}(p) > p · \log_2 \, (1/p)$ is valid. |
| − | + $H_{\rm bin}(p) - p · \log_2 \, (1/p)$ | + | + $H_{\rm bin}(p) - p · \log_2 \, (1/p)$ becomes smaller the smaller $p$ is. |
| − | { | + | {Which of the following equations are upper bounds on the rate? |
|type="[]"} | |type="[]"} | ||
+ $R/C ≤ [1 – H_{\rm bin}(p_{\rm B})]^{ –1 }$, | + $R/C ≤ [1 – H_{\rm bin}(p_{\rm B})]^{ –1 }$, | ||
+ $R′/C ≤ [1 + p_{\rm B} · \log_2 (p_{\rm B})]^{ –1 }$, | + $R′/C ≤ [1 + p_{\rm B} · \log_2 (p_{\rm B})]^{ –1 }$, | ||
+ $R′′/C ≤ 1 – p_{\rm B} · \log_2 (p_{\rm B})$, | + $R′′/C ≤ 1 – p_{\rm B} · \log_2 (p_{\rm B})$, | ||
| − | + $R′′′/C ≤ 1 + i · p_{\rm B}/ \lg(2)$ | + | + $R′′′/C ≤ 1 + i · p_{\rm B}/ \lg(2)$ für $p_{\rm B} = 10^{ –i}$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' According to the given equation: |
:$$ p_{\rm B,\hspace{0.05cm} min} = H_{\rm bin}^{-1} \left (1 - \frac{C}{R} \right) = H_{\rm bin}^{-1} (0.75) \hspace{0.05cm}.$$ | :$$ p_{\rm B,\hspace{0.05cm} min} = H_{\rm bin}^{-1} \left (1 - \frac{C}{R} \right) = H_{\rm bin}^{-1} (0.75) \hspace{0.05cm}.$$ | ||
| − | + | *From the graph on the data page (blue marking) we can read: | |
| + | :$$ p_{\rm B,\hspace{0.05cm} min} \hspace{0.15cm} \underline {=0.215} \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | |
| + | '''(2)''' By rearranging the above equation, we obtain with $H_{\rm bin}(p_{\rm B})$ from the graph: | ||
:$$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ | :$$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ | ||
\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$ | \Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$ | ||
| − | '''(3)''' | + | |
| − | * | + | '''(3)''' The <u>proposed solutions 2 and 3</u> are correct: |
| + | *For the binary entropy function, by definition: | ||
:$$H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | :$$H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | ||
| − | * | + | *Both terms are positive. From this follows the <u>proposed solution 2</u>: $H_{\rm bin}(p) > p · \log_2 \, (1/p)$. |
| − | * | + | *The difference is given by the second term of the binary entropy function: |
:$$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | :$$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$ | ||
| − | + | *This term becomes smaller the smaller $p$ is. | |
| − | :$$ p_{\rm B} | + | *The <u>proposed solution 3</u> is therefore also correct, as the following calculations show: |
| − | :$$p_{\rm B} | + | :$$ p_{\rm B} = 10^{-3}\text{:} \hspace{0.3cm} 0.999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.999}= 1.4420 \cdot 10^{-3} \hspace{0.05cm},$$ |
| − | :$$p_{\rm B | + | :$$p_{\rm B} = 10^{-4}\text{:} \hspace{0.3cm} 0.9999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9999}= 1.4427 \cdot 10^{-4} \hspace{0.05cm},$$ |
| + | :$$p_{\rm B} = 10^{-5}\text{:} \hspace{0.3cm} 0.99999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.99999}= 1.4427 \cdot 10^{-5} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' <u>All proposed solutions</u> are correct: | ||
| + | *The expression $R/C$ gives the upper bound according to the inverse channel coding theorem. | ||
| + | *For $p_{\rm B} = 10^{ –3 }$, the following bound is obtained: | ||
| + | :$$R/C ≤ 1.01154 \hspace{0.5cm} ⇒ \hspace{0.5cm} R/C - 1 ≤ 1.154 · 10^{ –2 }.$$ | ||
| + | * Proposition 2 takes into account the approximation according to subtask '''(3)''' . Since the denominator is now increased, $R′/C < R/C$, for example, applies for | ||
| + | :$$p_{\rm B} = 10^{ –3 }\text{:}\hspace{0.5cm} R′/C = 1.01007 · 10^{ –2 }.$$ | ||
| + | : This is also an upper bound, somewhat safer than the first bound $R/C$. | ||
| + | * The bound $R′′ < R′$ is obtained by replacing $1/(1 – ε)$ by $1 + ε$ $(ε$ is positive$)$. For example, for $p_{\rm B} = 10^{–3}$ one obtains | ||
| + | :$$R′′/C = 1.00997 \hspace{0.5cm} ⇒ \hspace{0.5cm} R′′/C - 1 ≤ 0.997 · 10^{–2}.$$ | ||
| + | * $R′′′$ according to the last suggestion is identical to $R′′$ and well suited for rollover calculations with integer exponent $i$ . <br>For the logarithm to the base ten, the numerical value $\lg(2) ≈ 0.30103$ applies. | ||
| + | |||
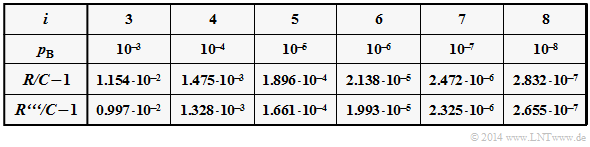
| + | [[File:P_ID2806__Inf_A_3_12d.png|right|frame|Calculated bounds for the code rates; $p_{\rm B} = 10^{ –i}$ applies]] | ||
| − | + | The table shows for different bit error probabilities $p_{\rm B}$ the deviations | |
| − | + | * of the first bound $(R/C-1)$ and | |
| − | * | + | * of the last approximation $(R'''/C-1)$. |
| − | * | ||
| − | |||
| − | |||
| − | + | One can see the good agreement of both specifications. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 95: | Line 117: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^3.3 Application to Digital Signal Transmission^]] |
Latest revision as of 12:57, 24 September 2021
Claude E. Shannon's channel coding theorem states, among other things, that a channel can be used to transmit with an arbitrarily small block error probability as long as the code rate $R$ is not greater than the channel capacity $C$. However, this result can only be achieved with channel coding for very large block lengths: $n → ∞$, which is associated with an arbitrarily large effort.
This statement is based on information-theoretical laws that Shannon himself established. However, Shannon does not say what this "infinitely good" channel coding must look like, he only proves that it exists.
The inverse of the channel coding theorem states that no error-free transmission is possible with a rate $R > C$. There is then no coding system with a vanishingly small error probability, no matter how elaborate and sophisticated the coding.
Rather, two bounds can be specified for the case $R > C$ :
- If one transmits via a "discrete memoryless channel" $\rm (DMC)$ with a rate $R$ greater than the channel capacity $C$, there is a lower bound for the bit error probability:
- $$ p_{\rm B} \ge H_{\rm bin}^{-1} \left (1 - {C}/{R} \right) > 0 \hspace{0.05cm}.$$
- If the bit error probability is not to exceed the value $p_{\rm B}$ after best possible decoding, the rate must not exceed a certain limit:
- $$ R \le \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.05cm}.$$
In this exercise, these equations are to be evaluated numerically using the binary entropy function
- $$ H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}.$$
$H_{\rm bin}(p)$ is sketched above. Because of $0 < p_B ≤ 1$ and $0 < C/R < 1$ the argument of the function $H_{\rm bin}(⋅)$ and its inverse $H_{\rm bin}^{ –1 }(⋅)$ is always between $0$ and $1$.
Hints:
- The exercise belongs to the chapter Application to digital signal transmission.
- Reference is made in particular to the page Rate, channel capacity and bit error probability.
- The values of the binary entropy function are provided, for example, by the (German language) interactive SWF applet
Entropien und Näherungen von digitalen Nachrichtenquellen ⇒ "Entropies and approximations of digital sources".
Questions
Solution
- $$ p_{\rm B,\hspace{0.05cm} min} = H_{\rm bin}^{-1} \left (1 - \frac{C}{R} \right) = H_{\rm bin}^{-1} (0.75) \hspace{0.05cm}.$$
- From the graph on the data page (blue marking) we can read:
- $$ p_{\rm B,\hspace{0.05cm} min} \hspace{0.15cm} \underline {=0.215} \hspace{0.05cm}.$$
(2) By rearranging the above equation, we obtain with $H_{\rm bin}(p_{\rm B})$ from the graph:
- $$\begin{align*} R_{\rm max} = \frac{C}{1 - H_{\rm bin}( p_{\rm B})} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.10:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.469}\hspace{0.15cm} \underline {=0.942} \hspace{0.05cm},\\ \Rightarrow \hspace{0.3cm} p_{\rm B} &= 0.05:\hspace{0.2cm} R_{\rm max} = \frac{0.5}{1 - 0.286}\hspace{0.15cm} \underline {=0.700}\hspace{0.05cm}.\end{align*}$$
(3) The proposed solutions 2 and 3 are correct:
- For the binary entropy function, by definition:
- $$H_{\rm bin}( p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- Both terms are positive. From this follows the proposed solution 2: $H_{\rm bin}(p) > p · \log_2 \, (1/p)$.
- The difference is given by the second term of the binary entropy function:
- $$ H_{\rm bin}( p) - p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} = (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$
- This term becomes smaller the smaller $p$ is.
- The proposed solution 3 is therefore also correct, as the following calculations show:
- $$ p_{\rm B} = 10^{-3}\text{:} \hspace{0.3cm} 0.999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.999}= 1.4420 \cdot 10^{-3} \hspace{0.05cm},$$
- $$p_{\rm B} = 10^{-4}\text{:} \hspace{0.3cm} 0.9999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9999}= 1.4427 \cdot 10^{-4} \hspace{0.05cm},$$
- $$p_{\rm B} = 10^{-5}\text{:} \hspace{0.3cm} 0.99999 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.99999}= 1.4427 \cdot 10^{-5} \hspace{0.05cm}.$$
(4) All proposed solutions are correct:
- The expression $R/C$ gives the upper bound according to the inverse channel coding theorem.
- For $p_{\rm B} = 10^{ –3 }$, the following bound is obtained:
- $$R/C ≤ 1.01154 \hspace{0.5cm} ⇒ \hspace{0.5cm} R/C - 1 ≤ 1.154 · 10^{ –2 }.$$
- Proposition 2 takes into account the approximation according to subtask (3) . Since the denominator is now increased, $R′/C < R/C$, for example, applies for
- $$p_{\rm B} = 10^{ –3 }\text{:}\hspace{0.5cm} R′/C = 1.01007 · 10^{ –2 }.$$
- This is also an upper bound, somewhat safer than the first bound $R/C$.
- The bound $R′′ < R′$ is obtained by replacing $1/(1 – ε)$ by $1 + ε$ $(ε$ is positive$)$. For example, for $p_{\rm B} = 10^{–3}$ one obtains
- $$R′′/C = 1.00997 \hspace{0.5cm} ⇒ \hspace{0.5cm} R′′/C - 1 ≤ 0.997 · 10^{–2}.$$
- $R′′′$ according to the last suggestion is identical to $R′′$ and well suited for rollover calculations with integer exponent $i$ .
For the logarithm to the base ten, the numerical value $\lg(2) ≈ 0.30103$ applies.
The table shows for different bit error probabilities $p_{\rm B}$ the deviations
- of the first bound $(R/C-1)$ and
- of the last approximation $(R'''/C-1)$.
One can see the good agreement of both specifications.