Difference between revisions of "Aufgaben:Exercise 2.1Z: Which Tables Describe Groups?"
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Some_Basics_of_Algebra}} |
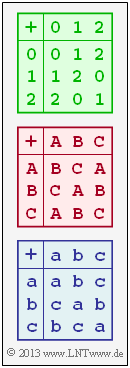
| − | [[File:P_ID2491__KC_Z_2_1.png|right|frame| | + | [[File:P_ID2491__KC_Z_2_1.png|right|frame|Addition tables for $q = 3$]] |
| − | In | + | In this exercise we consider sets of three elements each, generally denoted by $\{z_0, \, z_1, \, z_2\}$. The elements can be: |
| − | * | + | * numbers, for example $z_0 = 0, \ z_1 = 1, \ z_2 = 2$, |
| − | |||
| − | |||
| + | * algebraic expressions, such as $z_0 = A, \ z_1 = B, \ z_2 = C$, | ||
| − | + | * anything, for example $z_0 = \ "\hspace{-0.05cm}{\rm apple}\hspace{-0.05cm}", \ z_1 = \ "\hspace{-0.05cm}{\rm pear}\hspace{-0.05cm}", \ z_2 = \ "\hspace{-0.05cm}{\rm lemon}\hspace{-0.05cm}"$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A group $(G, \ "+")$ with respect to the addition results if by a table the "$+$"–linkage between two elements each was defined in such a way that the following conditions are fulfilled $($the control variables $i, \ j, \ k$ can take the values $0, \ 1, \ 2$ respectively): | |
| − | + | * For all $z_i ∈ G$ and $z_j ∈ G$ holds $(z_i + z_j) ∈ G$ ⇒ "closure criterion". The condition must also be satisfied for $i = j$. | |
| − | :$${\rm Inv_A}(0) = 0 \hspace{0.05cm},\hspace{0. | + | |
| − | \hspace{0.05cm},\hspace{0. | + | * For all $z_i, \ z_j, \ z_k$: $(z_i + z_j) + z_k = z_i + (z_j + z_k)$ ⇒ "Associative law". |
| + | |||
| + | * There is a "neutral element with respect to addition" ⇒ $N_{\rm A} ∈ G$ such that for all $z_i ∈ G$ holds $z_i + N_{\rm A} = z_i$. | ||
| + | |||
| + | * For all $z_i ∈ G$ there is a "inverse element with respect to addition" ⇒ ${\rm Inv}_{\rm A}(z_i) ∈ G$ such that $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A}$ holds. | ||
| + | |||
| + | |||
| + | If, in addition, for all $z_i ∈ G$ and $z_j ∈ G$ still the "commutative law" ⇒ $z_i + z_j = z_j + z_i$ is satisfied, then it is called a "commutative group" or – after the Norwegian mathematician [https://en.wikipedia.org/wiki/Niels_Henrik_Abel Niels Hendrik Abel] – an "Abelian group". | ||
| + | |||
| + | The number set $\{0, \, 1, \, 2\}$ is an Abelian (commutative) group. | ||
| + | *According to the green bordered addition table in the above diagram, the addition modulo $3$ is to be understood here. | ||
| + | *So the sum is always $0, \ 1$ or $2$. | ||
| + | *The neutral element is $N_{\rm A} = 0$ and the to $z_i$ inverse element ${\rm Inv}_{\rm A}(z_i) = -z_i$: | ||
| + | :$${\rm Inv_A}(0) = 0 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(1) = (-1)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 2 | ||
| + | \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(2) = (-2)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 1 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In | + | In this exercise, you are to check whether the two other addition tables shown in the above diagram also each belong to an "algebraic group". |
| + | |||
| + | Hints: | ||
| + | * The exercise belongs to the chapter [[Channel_Coding/Some_Basics_of_Algebra|"Some Basics of Algebra"]]. | ||
| − | + | * Reference is made in particular to the page [[Channel_Coding/Some_Basics_of_Algebra#Definition_and_examples_of_an_algebraic_group|"Definition and examples of an algebraic group"]]. | |
| − | * | ||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements result from the <u>red bordered</u> addition table? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The neutral element is $N_{\rm A} = {\rm C}$. |
| − | + | + | + The inverses are $\rm Inv_A(A) = B, \ \ Inv_A(B) = A, \ \ Inv_A(C) = C$. |
| − | + | + | + This is an additive group $(G, \ +)$. |
| − | + | + | + The condition of an Abelian group is also satisfied. |
| − | { | + | {Does anything change from subtask '''(1)''' if the elements $\rm A, \ \ B, \ \ C$ now stand for "$\hspace{-0.01cm}\rm apple\hspace{0.01cm}$", "$\rm pear$" and "$\rm lemon$" ? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes. |
| − | + | + | + No. |
| − | { | + | {What statements result from the <u>blue bordered</u> addition table? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The neutral element is $N_{\rm A} = a$. |
| − | + | + | + The additive inverses are $\rm Inv_A(a) = a, \ \ Inv_A(b) = b, \ \ Inv_A(c) = c$. |
| − | - | + | - This is an Abelian group. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>All statements</u> are true: |
| − | * | + | *The neutral element $N_{\rm A} = {\rm C}$ can be recognized from the last row of the addition table. |
| − | * | + | |
| − | :* $\rm Inv_A(A) = B$, | + | *From the condition $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A} = {\rm C}$ one obtains: |
| − | :* $\rm Inv_A(B) = A$, | + | :* $\rm Inv_A(A) = B$, since the second position of the first row contains the only $\rm C$, |
| − | :* $\rm Inv_A(C) = C$, | + | :* $\rm Inv_A(B) = A$, since the first position of the second row is the only $\rm C$, |
| − | * | + | :* $\rm Inv_A(C) = C$, since in the last position of the third row is the only $\rm C$. |
| + | *We check the "associative law" (improperly) on only one example. By applying the addition table twice, we get e.g. $\rm (A + B) + C = C + C=C$. The same result is obtained for $\rm A + (B + C) = A + B = C$. | ||
| + | |||
| + | |||
| + | Thus all conditions for an additive group are fulfilled. The validity of the commutative law can be seen from the symmetry of the addition table to the diagonal. Thus the group is also "Abelian". | ||
| + | By the way: The (red) addition table results from the green table by renaming $0 → \rm C, \ 1 → A$ and $2 → \rm B$ and then $\rm ABC$ sorting. | ||
| − | |||
| − | |||
| + | '''(2)''' Correct is <u>No</u>: | ||
| + | *All statements are determined by the addition table alone and not by the meaning of the elements. | ||
| + | |||
| + | *Even the author of this exercise, however, cannot justify more deeply why the modulo–3 addition of "$\rm apple$" and "$\rm pear$" yields the neutral element "$\rm lemon$". | ||
| − | |||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(3)''' The <u>first two statements</u> are true in contrast to the last one: |
| − | * | + | *The commutative law is violated (no symmetry with respect to the table diagonals). For example: |
:$$ {\rm a} + {\rm b} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm b} + {\rm a} = {\rm c} \hspace{0.05cm},$$ | :$$ {\rm a} + {\rm b} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm b} + {\rm a} = {\rm c} \hspace{0.05cm},$$ | ||
:$${\rm a} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$ | :$${\rm a} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$ | ||
:$${\rm b} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm b} = {\rm c} \hspace{0.05cm} \hspace{0.05cm}.$$ | :$${\rm b} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm b} = {\rm c} \hspace{0.05cm} \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus the linkage considered here is not an Abelian (commutative) group. |
| + | |||
| + | *Moreover, because of the violation of the "associative law", already the basic conditions of a group are not present here. For example: | ||
:$${\rm c} + ({\rm c} + {\rm c}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$ | :$${\rm c} + ({\rm c} + {\rm c}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$ | ||
:$$({\rm c} + {\rm c}) + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm a} + {\rm c} = {\rm c} \hspace{0.05cm}.$$ | :$$({\rm c} + {\rm c}) + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm a} + {\rm c} = {\rm c} \hspace{0.05cm}.$$ | ||
| Line 89: | Line 105: | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.1 Some Basics of Algebra^]] |
Latest revision as of 15:23, 27 August 2022
In this exercise we consider sets of three elements each, generally denoted by $\{z_0, \, z_1, \, z_2\}$. The elements can be:
- numbers, for example $z_0 = 0, \ z_1 = 1, \ z_2 = 2$,
- algebraic expressions, such as $z_0 = A, \ z_1 = B, \ z_2 = C$,
- anything, for example $z_0 = \ "\hspace{-0.05cm}{\rm apple}\hspace{-0.05cm}", \ z_1 = \ "\hspace{-0.05cm}{\rm pear}\hspace{-0.05cm}", \ z_2 = \ "\hspace{-0.05cm}{\rm lemon}\hspace{-0.05cm}"$.
A group $(G, \ "+")$ with respect to the addition results if by a table the "$+$"–linkage between two elements each was defined in such a way that the following conditions are fulfilled $($the control variables $i, \ j, \ k$ can take the values $0, \ 1, \ 2$ respectively):
- For all $z_i ∈ G$ and $z_j ∈ G$ holds $(z_i + z_j) ∈ G$ ⇒ "closure criterion". The condition must also be satisfied for $i = j$.
- For all $z_i, \ z_j, \ z_k$: $(z_i + z_j) + z_k = z_i + (z_j + z_k)$ ⇒ "Associative law".
- There is a "neutral element with respect to addition" ⇒ $N_{\rm A} ∈ G$ such that for all $z_i ∈ G$ holds $z_i + N_{\rm A} = z_i$.
- For all $z_i ∈ G$ there is a "inverse element with respect to addition" ⇒ ${\rm Inv}_{\rm A}(z_i) ∈ G$ such that $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A}$ holds.
If, in addition, for all $z_i ∈ G$ and $z_j ∈ G$ still the "commutative law" ⇒ $z_i + z_j = z_j + z_i$ is satisfied, then it is called a "commutative group" or – after the Norwegian mathematician Niels Hendrik Abel – an "Abelian group".
The number set $\{0, \, 1, \, 2\}$ is an Abelian (commutative) group.
- According to the green bordered addition table in the above diagram, the addition modulo $3$ is to be understood here.
- So the sum is always $0, \ 1$ or $2$.
- The neutral element is $N_{\rm A} = 0$ and the to $z_i$ inverse element ${\rm Inv}_{\rm A}(z_i) = -z_i$:
- $${\rm Inv_A}(0) = 0 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(1) = (-1)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 2 \hspace{0.05cm},\hspace{0.5cm}{\rm Inv_A}(2) = (-2)\hspace{0.15cm}{\rm mod}\hspace{0.15cm}3 = 1 \hspace{0.05cm}.$$
In this exercise, you are to check whether the two other addition tables shown in the above diagram also each belong to an "algebraic group".
Hints:
- The exercise belongs to the chapter "Some Basics of Algebra".
- Reference is made in particular to the page "Definition and examples of an algebraic group".
Questions
Solution
- The neutral element $N_{\rm A} = {\rm C}$ can be recognized from the last row of the addition table.
- From the condition $z_i + {\rm Inv}_{\rm A}(z_i) = N_{\rm A} = {\rm C}$ one obtains:
- $\rm Inv_A(A) = B$, since the second position of the first row contains the only $\rm C$,
- $\rm Inv_A(B) = A$, since the first position of the second row is the only $\rm C$,
- $\rm Inv_A(C) = C$, since in the last position of the third row is the only $\rm C$.
- We check the "associative law" (improperly) on only one example. By applying the addition table twice, we get e.g. $\rm (A + B) + C = C + C=C$. The same result is obtained for $\rm A + (B + C) = A + B = C$.
Thus all conditions for an additive group are fulfilled. The validity of the commutative law can be seen from the symmetry of the addition table to the diagonal. Thus the group is also "Abelian".
By the way: The (red) addition table results from the green table by renaming $0 → \rm C, \ 1 → A$ and $2 → \rm B$ and then $\rm ABC$ sorting.
(2) Correct is No:
- All statements are determined by the addition table alone and not by the meaning of the elements.
- Even the author of this exercise, however, cannot justify more deeply why the modulo–3 addition of "$\rm apple$" and "$\rm pear$" yields the neutral element "$\rm lemon$".
(3) The first two statements are true in contrast to the last one:
- The commutative law is violated (no symmetry with respect to the table diagonals). For example:
- $$ {\rm a} + {\rm b} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm b} + {\rm a} = {\rm c} \hspace{0.05cm},$$
- $${\rm a} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$
- $${\rm b} + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm b} \hspace{0.5cm} \ne \hspace{0.5cm} {\rm c} + {\rm b} = {\rm c} \hspace{0.05cm} \hspace{0.05cm}.$$
- Thus the linkage considered here is not an Abelian (commutative) group.
- Moreover, because of the violation of the "associative law", already the basic conditions of a group are not present here. For example:
- $${\rm c} + ({\rm c} + {\rm c}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm c} + {\rm a} = {\rm b} \hspace{0.05cm},$$
- $$({\rm c} + {\rm c}) + {\rm c} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm a} + {\rm c} = {\rm c} \hspace{0.05cm}.$$