Difference between revisions of "Aufgaben:Exercise 2.14: Petersen Algorithm?"
From LNTwww
| (14 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding}} |
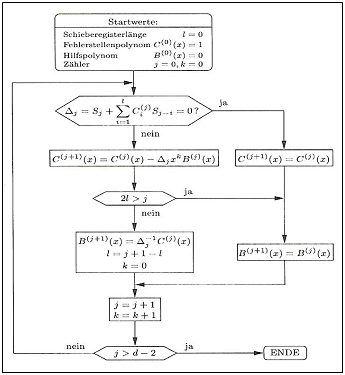
| − | [[File: P_ID2580__KC_A_2_14_v1.png|right|frame| | + | [[File: P_ID2580__KC_A_2_14_v1.png|right|frame|Chart from [Bos98]: <br>'''(1)''' Fast decoding algorithm for RS codes. <br>'''(2)''' It is therefore not the Petersen algorithm!]] |
| − | + | In the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding|"Error Correction According to Reed-Solomon Coding"]] the decoding of Reed–Solomon codes with the "Petersen algorithm" was treated. | |
| − | + | * Its advantage is that the individual steps are traceable. | |
| − | * | ||
| + | * Very much of disadvantage is however the immensely high decoding expenditure. | ||
| − | |||
| − | + | Already since the invention of Reed–Solomon coding in 1960, many scientists and engineers were engaged in the development of algorithms for Reed–Solomon decoding as fast as possible, and even today "Algebraic Decoding" is still a highly topical field of research. | |
| + | In this exercise, some related concepts will be explained. A detailed explanation of these procedures has been omitted in our "$\rm LNTwww $". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Hints: | ||
| + | * The exercise belongs to the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding| "Error Correction According to Reed-Solomon Coding"]]. | ||
| + | |||
| + | * The diagram shows the flowchart of one of the most popular methods for decoding Reed–Solomon codes. Which algorithm is mentioned in the sample solution to this exercise. | ||
| − | === | + | *The graphic was taken from the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998". We thank the author Martin Bossert for the permission to use the graphic. |
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {For which codes is syndrome decoding used? For |
|type="[]"} | |type="[]"} | ||
| − | + | + | + binary block codes, |
| − | - | + | - Reed–Solomon codes, |
| − | - | + | - convolutional codes. |
| − | { | + | {What is most complex in the Petersen algorithm? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Checking if there are $($one or more$)$ errors at all, |
| − | + | + | + the localization of the errors, |
| − | - | + | - the determination of the error value. |
| − | { | + | {Which terms refer to Reed–Solomon decoding? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The Berlekamp–Massey algorithm, |
| − | - | + | - the BCJR algorithm, |
| − | + | + | + the Euclidean algorithm, |
| − | + | + | + frequency domain methods based on the DFT, |
| − | - | + | - the Viterbi algorithm. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>answer 1</u>: |
| − | * | + | *In principle, a syndrome decoder would also be possible with Reed–Solomon codes, but with the large code word lengths $n$ common here, extremely long decoding times would result. |
| − | * | + | |
| + | *For convolutional codes (these work serially) syndrome decoding makes no sense at all. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' As can be seen from the discussion in the theory section, error localization involves by far the greatest effort ⇒ <u>Answer 2</u>. | ||
| + | |||
| − | '''( | + | '''(3)''' Correct <u>answers 1, 3, and 4</u>: |
| + | *These procedures are summarized in the [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Fast_Reed-Solomon_decoding| "Fast Reed–Solomon decoding"]] section. | ||
| + | |||
| + | *The BCJR– and Viterbi algorithms, on the other hand, refer to [[Channel_Coding/Decoding_of_Convolutional_Codes|"Decoding of convolutional codes"]]. | ||
| + | *The graphic in the information section shows the Berlekamp–Massey algorithm $\rm (BMA)$. | ||
| − | + | *The explanation of this figure can be found in the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998" from page 73. | |
| − | * | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.5 Reed-Solomon Error Correction^]] |
Latest revision as of 00:41, 13 November 2022
Chart from [Bos98]:
(1) Fast decoding algorithm for RS codes.
(2) It is therefore not the Petersen algorithm!
(1) Fast decoding algorithm for RS codes.
(2) It is therefore not the Petersen algorithm!
In the chapter "Error Correction According to Reed-Solomon Coding" the decoding of Reed–Solomon codes with the "Petersen algorithm" was treated.
- Its advantage is that the individual steps are traceable.
- Very much of disadvantage is however the immensely high decoding expenditure.
Already since the invention of Reed–Solomon coding in 1960, many scientists and engineers were engaged in the development of algorithms for Reed–Solomon decoding as fast as possible, and even today "Algebraic Decoding" is still a highly topical field of research.
In this exercise, some related concepts will be explained. A detailed explanation of these procedures has been omitted in our "$\rm LNTwww $".
Hints:
- The exercise belongs to the chapter "Error Correction According to Reed-Solomon Coding".
- The diagram shows the flowchart of one of the most popular methods for decoding Reed–Solomon codes. Which algorithm is mentioned in the sample solution to this exercise.
- The graphic was taken from the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998". We thank the author Martin Bossert for the permission to use the graphic.
Questions
Solution
(1) Correct is the answer 1:
- In principle, a syndrome decoder would also be possible with Reed–Solomon codes, but with the large code word lengths $n$ common here, extremely long decoding times would result.
- For convolutional codes (these work serially) syndrome decoding makes no sense at all.
(2) As can be seen from the discussion in the theory section, error localization involves by far the greatest effort ⇒ Answer 2.
(3) Correct answers 1, 3, and 4:
- These procedures are summarized in the "Fast Reed–Solomon decoding" section.
- The BCJR– and Viterbi algorithms, on the other hand, refer to "Decoding of convolutional codes".
- The graphic in the information section shows the Berlekamp–Massey algorithm $\rm (BMA)$.
- The explanation of this figure can be found in the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998" from page 73.
