Difference between revisions of "Aufgaben:Exercise 3.1Z: Triangular PDF"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (18 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Probability_Density_Function |
}} | }} | ||
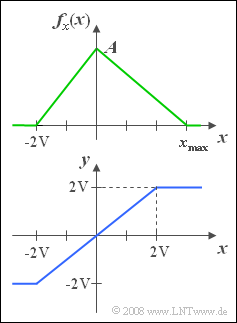
| − | [[File:P_ID109__Sto_Z_3_1.png|right| | + | [[File:P_ID109__Sto_Z_3_1.png|right|frame|Triangular PDF and <br>characteristic curve $y(x)$]] |
| − | + | We consider a continuous random variable $x$ with the PDF outlined on the right. | |
| + | *The minimum value of the signal is $x_{\rm min} = -2\hspace{0.05cm} {\rm V}$. | ||
| + | *On the other hand, the maximum value $x_{\rm max}$ is a free parameter, allowing values between $+2\hspace{0.05cm}\rm V$ and $+4\hspace{0.05cm} \rm V$. | ||
| − | |||
| − | |||
| − | + | The random variable $x$ is to be understood here as the instantaneous value of a random signal. If this signal $x(t)$ is applied to an amplitude limiter with the characteristic curve (see sketch below) | |
| + | :$$y(t)=\left\{\begin{array}{*{4}{c}} -2\hspace{0.05cm} {\rm V} & {\rm if}\hspace{0.1cm} x(t)<-2\hspace{0.05cm} {\rm V} , \\ x(t) & {\rm if}\hspace{0.1cm}-2\hspace{0.05cm} {\rm V} \le x(t)\le +2\hspace{0.05cm} {\rm V}, \\ +2\hspace{0.05cm} {\rm V} & {\rm if}\hspace{0.1cm} {\it x}({\it t})>+2\hspace{0.05cm} {\rm V}, \\\end{array}\right.$$ | ||
| − | + | so the signal $y(t)$ or the new random variable $y$, which is considered in the last two subquestions '''(5)''' and '''(6)''' is obtained. <br /> | |
| + | *For the subtasks '''(1)''' and '''(2)''' apply $x_{\rm max} = 2\hspace{0.05cm} {\rm V} $. | ||
| + | * For all other subtasks, set $x_{\rm max} = 4\hspace{0.05cm} {\rm V} $ . | ||
| − | + | ||
| − | * | + | |
| + | |||
| + | |||
| + | Hints: | ||
| + | *The task belongs to the chapter [[Theory_of_Stochastic_Signals/Probability_Density_Function|Probability Density Function]]. | ||
| − | * | + | *The topic of this chapter is illustrated with examples in the (German language) learning video <br> [[Wahrscheinlichkeit_und_WDF_(Lernvideo)|"Wahrscheinlichkeit und WDF"]] $\Rightarrow$ "Probability and PDF". |
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Let be $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$. Calculate the parameter $A = f_x(0)$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A \ = \ $ { 0.5 3% } $\ \rm 1/V$. |
| − | { | + | {Let $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$. What is the probability that $|x(t)|$ less than $x_{\rm max}/2$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| < 1\hspace{0.05cm} {\rm V}) \ = \ $ { 0.75 3% } |
| − | { | + | {Now let be $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$. What is the probability that $x$ lies between $+1\hspace{0.05cm} {\rm V}$ and $+3\hspace{0.05cm} {\rm V}$? |
|type="{}"} | |type="{}"} | ||
| − | + | ${\rm Pr}(1\hspace{0.05cm} {\rm V} < x <3\hspace{0.05cm} {\rm V}) \ = \ $ { 0.333 3% } | |
| − | { | + | { Let further be $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$. What is the probability that $x$ is exactly equal to $+2\hspace{0.05cm} {\rm V}$? |
|type="{}"} | |type="{}"} | ||
| − | + | ${\rm Pr}(x =2\hspace{0.05cm} {\rm V})\ = \ $ { 0. } | |
| − | { | + | { Let further be $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$. Which of the following statements is true? |
|type="[]"} | |type="[]"} | ||
| − | - $y$ | + | - $y$ is a continuous random variable. |
| − | - $y$ | + | - $y$ is a discrete random variable. |
| − | + $y$ | + | + $y$ is a mixed continuous-discrete random variable. |
| − | { | + | {Let further be $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$. What is the probability that $y$ is exactly equal $+2\hspace{0.05cm} {\rm V}$? |
|type="{}"} | |type="{}"} | ||
| − | + | ${\rm Pr}(y =2\hspace{0.05cm} {\rm V})\ = \ $ { 0.167 3% } | |
| + | |||
| Line 59: | Line 66: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
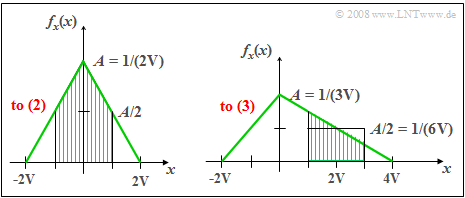
| − | '''(1)''' | + | [[File:EN_Sto_Z_3_1_bc.png|right|frame|Height and area of triangular PDF]] |
| − | $${A}/{ 2}\cdot {4\hspace{0. | + | '''(1)''' The area under the PDF must always yield the value $1$. It follows that: |
| + | :$${A}/{ 2}\cdot {4\hspace{0.05cm}\rm V}=1\hspace{0.5cm}\Rightarrow\hspace{0.5cm} A | ||
\hspace{0.15cm}\underline{=\rm 0.5\;{1}/{V}}.$$ | \hspace{0.15cm}\underline{=\rm 0.5\;{1}/{V}}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' | + | '''(2)''' With $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$ the PDF is obtained according to the left graph. |
| + | *The shading marks the probability we are looking for. | ||
| + | *One obtains by simple geometric considerations: | ||
| + | :$${\rm Pr}(|x|<\rm 1\hspace{0.05cm} V)\hspace{0.15cm}\underline{=\rm 0.75}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' With $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$ one obtains the PDF shown on the right. | ||
| + | *The maximum value is now $A = 1/(3\hspace{0.05cm} {\rm V})$. | ||
| + | *The shaded area again indicates the probability we are looking for, which can be determined using the rectangle of equal area: | ||
| + | :$${\rm Pr}(1\hspace{0.05cm} {\rm V}< x<3\hspace{0.05cm} {\rm V})=\rm \frac{1}{6\hspace{0.05cm} {\rm V}}\cdot 2\hspace{0.05cm} {\rm V}=\hspace{0.15cm}\underline{0.333}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Since $x$ represents a continuous random variable, this probability is by definition zero ⇒ ${\rm Pr}(x =2\hspace{0.05cm} {\rm V}) \;\underline {= 0}$. | ||
| + | |||
| + | |||
| + | |||
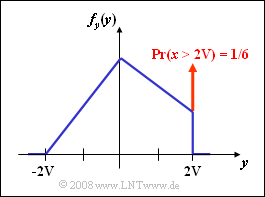
| + | [[File:P_ID113__Sto_Z_3_1_f.png|right|frame|Mixed continuous/discrete PDF]] | ||
| + | '''(5)''' <u>Only the last statement</u> of the given answers is true: | ||
| + | |||
| + | *The PDF $f_y(y)$ includes a continuous component (drawn in blue), | ||
| + | *but also the (red) Dirac delta function at $y = +2\hspace{0.05cm} {\rm V}$ with weight ${\rm Pr}(x >2\hspace{0.05cm} {\rm V})$. | ||
| − | |||
| − | |||
| − | |||
| − | '''(6)''' | + | '''(6)''' The graphic on the right shows the probability density function of the random variable $y$. |
| − | $${\rm Pr}( y=2\hspace{0.05cm} {\rm V} | + | *From the right figure for subtask '''(3)''' one can see the relation: |
| + | :$${\rm Pr}( y=2\hspace{0.05cm} {\rm V}) = {\rm Pr}( x> 2\hspace{0.05cm} {\rm V}) = \frac{1}{2}\cdot\frac{1}{6\hspace{0.05cm} {\rm V}}\cdot2{\hspace{0.05cm} {\rm V}} = {1}/{6}\hspace{0.15cm}\underline{=0.167}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.1 Probability Density Function^]] |
Latest revision as of 16:55, 8 February 2022
We consider a continuous random variable $x$ with the PDF outlined on the right.
- The minimum value of the signal is $x_{\rm min} = -2\hspace{0.05cm} {\rm V}$.
- On the other hand, the maximum value $x_{\rm max}$ is a free parameter, allowing values between $+2\hspace{0.05cm}\rm V$ and $+4\hspace{0.05cm} \rm V$.
The random variable $x$ is to be understood here as the instantaneous value of a random signal. If this signal $x(t)$ is applied to an amplitude limiter with the characteristic curve (see sketch below)
- $$y(t)=\left\{\begin{array}{*{4}{c}} -2\hspace{0.05cm} {\rm V} & {\rm if}\hspace{0.1cm} x(t)<-2\hspace{0.05cm} {\rm V} , \\ x(t) & {\rm if}\hspace{0.1cm}-2\hspace{0.05cm} {\rm V} \le x(t)\le +2\hspace{0.05cm} {\rm V}, \\ +2\hspace{0.05cm} {\rm V} & {\rm if}\hspace{0.1cm} {\it x}({\it t})>+2\hspace{0.05cm} {\rm V}, \\\end{array}\right.$$
so the signal $y(t)$ or the new random variable $y$, which is considered in the last two subquestions (5) and (6) is obtained.
- For the subtasks (1) and (2) apply $x_{\rm max} = 2\hspace{0.05cm} {\rm V} $.
- For all other subtasks, set $x_{\rm max} = 4\hspace{0.05cm} {\rm V} $ .
Hints:
- The task belongs to the chapter Probability Density Function.
- The topic of this chapter is illustrated with examples in the (German language) learning video
"Wahrscheinlichkeit und WDF" $\Rightarrow$ "Probability and PDF".
Questions
Solution
(1) The area under the PDF must always yield the value $1$. It follows that:
- $${A}/{ 2}\cdot {4\hspace{0.05cm}\rm V}=1\hspace{0.5cm}\Rightarrow\hspace{0.5cm} A \hspace{0.15cm}\underline{=\rm 0.5\;{1}/{V}}.$$
(2) With $x_{\rm max} = +2\hspace{0.05cm} {\rm V}$ the PDF is obtained according to the left graph.
- The shading marks the probability we are looking for.
- One obtains by simple geometric considerations:
- $${\rm Pr}(|x|<\rm 1\hspace{0.05cm} V)\hspace{0.15cm}\underline{=\rm 0.75}.$$
(3) With $x_{\rm max} = +4\hspace{0.05cm} {\rm V}$ one obtains the PDF shown on the right.
- The maximum value is now $A = 1/(3\hspace{0.05cm} {\rm V})$.
- The shaded area again indicates the probability we are looking for, which can be determined using the rectangle of equal area:
- $${\rm Pr}(1\hspace{0.05cm} {\rm V}< x<3\hspace{0.05cm} {\rm V})=\rm \frac{1}{6\hspace{0.05cm} {\rm V}}\cdot 2\hspace{0.05cm} {\rm V}=\hspace{0.15cm}\underline{0.333}.$$
(4) Since $x$ represents a continuous random variable, this probability is by definition zero ⇒ ${\rm Pr}(x =2\hspace{0.05cm} {\rm V}) \;\underline {= 0}$.
(5) Only the last statement of the given answers is true:
- The PDF $f_y(y)$ includes a continuous component (drawn in blue),
- but also the (red) Dirac delta function at $y = +2\hspace{0.05cm} {\rm V}$ with weight ${\rm Pr}(x >2\hspace{0.05cm} {\rm V})$.
(6) The graphic on the right shows the probability density function of the random variable $y$.
- From the right figure for subtask (3) one can see the relation:
- $${\rm Pr}( y=2\hspace{0.05cm} {\rm V}) = {\rm Pr}( x> 2\hspace{0.05cm} {\rm V}) = \frac{1}{2}\cdot\frac{1}{6\hspace{0.05cm} {\rm V}}\cdot2{\hspace{0.05cm} {\rm V}} = {1}/{6}\hspace{0.15cm}\underline{=0.167}.$$