Difference between revisions of "Aufgaben:Exercise 3.6: Transient Behavior"
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (43 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform |
}} | }} | ||
| − | [[File:P_ID1784__LZI_A_3_6.png|right|frame| | + | [[File:P_ID1784__LZI_A_3_6.png|right|frame|Cosine and sine waves, each causal]] |
| − | + | In this exercise, we consider a cosine signal $c(t)$ with amplitude $1$ and period $T = 1 \ \rm µ s$, which is defined for all times $t$ $($in the range $ \pm \infty)$ : | |
:$$c(t) = \cos(2\pi \cdot {t}/{T}) | :$$c(t) = \cos(2\pi \cdot {t}/{T}) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | The causal $($German: "kausal" ⇒ subscript "K"$)$ cosine signal $c_{\rm K}(t)$ (red curve) starts only at the turn-on instant $t = 0$: | |
:$$c_{\rm K}(t)= \left\{ \begin{array}{c} c(t) \\ | :$$c_{\rm K}(t)= \left\{ \begin{array}{c} c(t) \\ | ||
0 \end{array} \right. | 0 \end{array} \right. | ||
| − | \begin{array}{c} {\rm{ | + | \begin{array}{c} {\rm{for}} \\ {\rm{for}} |
\end{array}\begin{array}{*{20}c} | \end{array}\begin{array}{*{20}c} | ||
{ t \ge 0\hspace{0.05cm},} \\ | { t \ge 0\hspace{0.05cm},} \\ | ||
{ t < 0\hspace{0.05cm}.} | { t < 0\hspace{0.05cm}.} | ||
\end{array}$$ | \end{array}$$ | ||
| − | + | Only the Fourier spectrum can be specified for the bilaterally unbounded signal $c(t)$: | |
:$$C(f) = {1}/{ 2} \cdot \delta (f - f_0) + {1}/{ 2} \cdot \delta (f + f_0) | :$$C(f) = {1}/{ 2} \cdot \delta (f - f_0) + {1}/{ 2} \cdot \delta (f + f_0) | ||
| − | \quad {\rm | + | \quad {\rm with} \quad f_0 = {1}/{ T}= 1\,\,{\rm MHz.}$$ |
| − | + | On the contrary, for the causal cosine signal $c_{\rm K}(t)$ the Laplace transform can also be specified: | |
:$$C_{\rm L}(p) = | :$$C_{\rm L}(p) = | ||
\frac {p} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$ | \frac {p} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$ | ||
| − | + | Accordingly, the following holds for the Laplace transform of the causal sine function $s_{\rm K}(t)$: | |
:$$S_{\rm L}(p) = | :$$S_{\rm L}(p) = | ||
\frac {2 \pi/T} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$ | \frac {2 \pi/T} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$ | ||
| − | + | The bilaterally unbounded sine function is denoted by $s(t)$ and is shown as a blue–dotted curve in the below diagram. | |
| − | + | The signals $c(t)$, $c_{\rm K}(t)$, $s(t)$ and $s_{\rm K}(t)$ are applied to the input of a low-pass filter of first-order with the following transfer function (or impulse response): | |
:$$H_{\rm L}(p) = | :$$H_{\rm L}(p) = | ||
\frac {2 /T} { p + 2 /T} \quad | \frac {2 /T} { p + 2 /T} \quad | ||
\bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad | \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad | ||
h(t) = {2}/{T} \cdot {\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 | h(t) = {2}/{T} \cdot {\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 | ||
| − | \hspace{0.03cm}t/T}$$ | + | \hspace{0.03cm}t/T}.$$ |
| − | + | *The corresponding output signals are denoted by $y_{\rm C}(t)$, $y_{\rm CK}(t)$, $y_{\rm S}(t)$ and $y_{\rm SK}(t)$ . | |
| + | *These signals are to be computed and correlated to each other in this exercise. | ||
| + | |||
| + | |||
| + | |||
| Line 39: | Line 43: | ||
| − | + | Please note: | |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. |
| − | + | *The computations for subtask '''(6)''' are bulky. | |
| − | * | + | *For computing the signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$, for example the [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Formulation_of_the_residue_theorem|residue theorem]] can be used. |
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Compute the frequency response $H(f)$ by magnitude and phase using $H_{\rm L}(p)$. What values are obtained for frequency $ f = f_0 = 1/T = 1 \ \rm MHz$? |
|type="{}"} | |type="{}"} | ||
$|H(f = f_0)| \ = \ $ { 0.303 3% } | $|H(f = f_0)| \ = \ $ { 0.303 3% } | ||
$a(f = f_0)\hspace{0.2cm} = \ $ { 1.194 3% } $\ \rm Np$ | $a(f = f_0)\hspace{0.2cm} = \ $ { 1.194 3% } $\ \rm Np$ | ||
| − | $ | + | ${\rm arc} \ H(f = f_0)\ = \ $ { -74--70 } $\ \rm deg$ |
| − | $ | + | $b(f = f_0)\hspace{0.24cm} = \ $ { 72 3% } $\ \rm deg$ |
| − | { | + | {Compute the signal $y_{\rm C}(t)$ at the filter output if the cosine signal $c(t)$ is applied to the filter input. What value is obtained for $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y_{\rm C}(t = 0) \ = \ $ { 0.092 3% } | $y_{\rm C}(t = 0) \ = \ $ { 0.092 3% } | ||
| − | { | + | {Compute the output signal $y_{\rm S}(t)$ if the sine signal $s(t)$ is applied to the filter input. What value is obtained for $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y_{\rm S}(t = 0) \ = \ $ { -0.295--0.283 } | $y_{\rm S}(t = 0) \ = \ $ { -0.295--0.283 } | ||
| − | { | + | {Determine the influence length $T_h$ of the filter impulse response, that is the time at which $h(t)$ has decayed to $1\%$ of the maximum value. Normalization to $T$. |
|type="{}"} | |type="{}"} | ||
$T_h/T \ = \ $ { 2.3 3% } | $T_h/T \ = \ $ { 2.3 3% } | ||
| − | { | + | {Which statements are true for the signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The following holds: $y_{\rm CK}(t) \equiv 0$ and $y_{\rm SK}(t) \equiv 0$ for $t < 0$. |
| − | + | + | + The signal $y_{\rm CK}(t)$ is approximately equal to $y_{\rm C}(t)$ for $t > T_h$ . |
| − | - | + | - The causal signal $y_{\rm SK}(t)$ is approximately equal to $y_{\rm S}(t)$ for $t < T_h$ . |
| − | { | + | {Using the residue theorem compute the signal $y_{\rm CK}(t)$ after the filter if $c_{\rm K}(t)$ is applied to the input. What signal value occurs at time $t = T/5$ ? |
|type="{}"} | |type="{}"} | ||
$y_\text{CK}(t = T/5) \ = \ $ { 0.24 3% } | $y_\text{CK}(t = T/5) \ = \ $ { 0.24 3% } | ||
| Line 87: | Line 90: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Replacing the parameter $T$ by $1/f_0$ and $p$ by ${\rm j} \cdot 2 \pi f$ in $H_{\rm L}(p)$ the following is obtained for the frequency response in general or for $f_0 = 1 \ \rm MHz$: |
:$$H(f) = \frac {2 /T} { {\rm j} \cdot 2 \pi f + 2 /T}= | :$$H(f) = \frac {2 /T} { {\rm j} \cdot 2 \pi f + 2 /T}= | ||
\frac {f_0} { {\rm j} \cdot \pi f + f_0} | \frac {f_0} { {\rm j} \cdot \pi f + f_0} | ||
| Line 102: | Line 105: | ||
| − | '''(2)''' | + | |
| + | '''(2)''' The output signal $y_{\rm C}(t)$ is attenuated by the factor $0.303$ and delayed by $\tau \approx 72/360 \cdot T = T/5$ compared to the input signal $c(t)$ . | ||
| + | |||
| + | *Thus, this signal can also be described as follows: | ||
:$$y_{\rm C}(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 | :$$y_{\rm C}(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 | ||
}}= 0.303 \cdot \cos(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm C}(t=0) = \frac {1} { {1 + \pi^2 | }}= 0.303 \cdot \cos(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm C}(t=0) = \frac {1} { {1 + \pi^2 | ||
}} \hspace{0.15cm}\underline{\approx 0.092} \hspace{0.05cm}.$$ | }} \hspace{0.15cm}\underline{\approx 0.092} \hspace{0.05cm}.$$ | ||
| − | + | *This signal is shown dotted in blue in the left graph for solution '''(5)'''. | |
| − | |||
| − | + | '''(3)''' The signal $y_{\rm S}(t)$ is also smaller by the attenuation factor $0.303$ and delayed by the time period $\tau = T/5$ compared to $s(t)$ . | |
| + | |||
| + | *It can be described as follows: | ||
:$$y_{\rm S}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})} { {1 + \pi^2 | :$$y_{\rm S}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})} { {1 + \pi^2 | ||
}}= 0.303 \cdot \sin(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm S}(t=0) = -\frac {\pi} { {1 + \pi^2 | }}= 0.303 \cdot \sin(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm S}(t=0) = -\frac {\pi} { {1 + \pi^2 | ||
}} \hspace{0.15cm}\underline{\approx -0.289} \hspace{0.05cm}.$$ | }} \hspace{0.15cm}\underline{\approx -0.289} \hspace{0.05cm}.$$ | ||
| − | + | *This signal is sketched dotted in blue in the right graph for solution '''(5)''' . | |
| − | '''(4)''' | + | |
| + | '''(4)''' At $T_h$ the impulse response $h(t)$ should have decayed to $1\%$ of the maximum value. Thus, the following holds: | ||
:$${\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 | :$${\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 | ||
\hspace{0.03cm}T_{ h}/T} = 0.01 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {T_{ h}}/{T} =\frac{1}{2} | \hspace{0.03cm}T_{ h}/T} = 0.01 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {T_{ h}}/{T} =\frac{1}{2} | ||
| Line 126: | Line 134: | ||
{0.02}/{T}\hspace{0.05cm}.$$ | {0.02}/{T}\hspace{0.05cm}.$$ | ||
| + | [[File:P_ID1785__LZI_A_3_6_e.png|right|frame|Transient behavior of a causal cosine and a causal sine signal]] | ||
| + | <br>'''(5)''' The <u>statements 1 and 2</u> are correct: | ||
| + | *The causal signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$ must be identical to zero for $t < 0$ . | ||
| + | *However, since the impulse response $h(t)$ of the considered filter (nearly) vanishes for $t > T_h$, it does not matter whether the unbounded cosine signal $c(t)$ or the causal signal $c_{\rm K}(t)$ is applied to the input after the transient effect is over. | ||
| + | *The same is true for the sinusoidal signals: For $t >T_{ h}$, $y_{\rm SK}(t)=y_{\rm S}(t)$ holds. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The graph shows the output signals $y_{\rm C}(t)$ and $y_{\rm CK}(t)$ for cosine-shaped input on the left and the signals $y_{\rm S}(t)$ and $y_{\rm SK}(t)$ for sinusoidal input on the right. '''Note the transit time''' of $T/5$ $($corresponding to the phase $72^\circ)$ '''in both cases'''. | |
| + | *For $y_{\rm CK}(t)$ the first wave peaks are smaller than $1$ to achieve the correct phase position of $y_{\rm C}(t)$ . | ||
| + | *In contrast, for $y_{\rm SK}(t)$ the first wave peaks are greater than $1$ to achieve the correct phase position of $y_{\rm S}(t)$ . | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(6)''' Considering | |
| − | '''(6)''' | + | $p_{\rm x1}= {\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm}p_{\rm x2}= -{\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm} |
| − | $p_{\rm x1}= {\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm}p_{\rm x2}= -{\rm j} \cdot {2\pi}/{T} | ||
p_{\rm x3}= -{2}/{T} | p_{\rm x3}= -{2}/{T} | ||
| − | \hspace{0.05cm}$ | + | \hspace{0.05cm}$ |
| − | + | the following can be written for the Laplace transform of the signal $y_{\rm CK}(t)$ : | |
:$$Y_{\rm L}(p) = | :$$Y_{\rm L}(p) = | ||
\frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})(p-p_{{\rm x}3})} | \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})(p-p_{{\rm x}3})} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The time function $y_{\rm CK}(t)$ is thus composed of three parts according to the residue theorem: | |
| − | * | + | * Considering $p_{\rm x2}= -p_{\rm x1}$ the first part is |
:$$y_1(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} | :$$y_1(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} | ||
\hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= | \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= | ||
| Line 165: | Line 172: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | * Similarly, the following is obtained for the second part: |
:$$y_2(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} | :$$y_2(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} | ||
\hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= | \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= | ||
| Line 178: | Line 185: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | * Combining both parts and considering the numerical values of $p_{\rm x1}$ and $p_{\rm x3}$: |
:$$y_{1\hspace{0.03cm}+2}(t)= \frac {1/T} { 2/T + {\rm j} \cdot 2\pi /T} | :$$y_{1\hspace{0.03cm}+2}(t)= \frac {1/T} { 2/T + {\rm j} \cdot 2\pi /T} | ||
\cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm} t/T}+\frac {1/T} { 2/T - {\rm j} \cdot 2\pi /T} | \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm} t/T}+\frac {1/T} { 2/T - {\rm j} \cdot 2\pi /T} | ||
| Line 192: | Line 199: | ||
\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi | ||
\hspace{0.03cm}t/T} | \hspace{0.03cm}t/T} | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm} $$ |
| − | * | + | * Using Euler's theorem this can also be expressed as follows: |
:$$y_{1\hspace{-0.03cm}+2} (t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 | :$$y_{1\hspace{-0.03cm}+2} (t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 | ||
}}= y_{\rm C}(t)\hspace{0.05cm}.$$ | }}= y_{\rm C}(t)\hspace{0.05cm}.$$ | ||
| − | + | :It can be seen that $y_{1\hspace{0.03cm}+2}(t)$ is equal to the signal $y_{\rm C}(t)$ computed in subtask '''(2)''' . | |
| − | * | + | * Finally, the following is obtained for the last residual: |
:$$y_3(t)=\frac {-p_{{\rm x}3}^2} { (p_{{\rm x}3}-p_{{\rm | :$$y_3(t)=\frac {-p_{{\rm x}3}^2} { (p_{{\rm x}3}-p_{{\rm | ||
x}1}) (p_{{\rm x}3}-p_{{\rm x}2})} \cdot {\rm | x}1}) (p_{{\rm x}3}-p_{{\rm x}2})} \cdot {\rm | ||
| Line 213: | Line 220: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | * Thus, the output signal is as follows for a causal cosine signal applied to the input: |
:$$y_{\rm CK}(t) = y_1(t)+y_2(t)+y_3(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})-{\rm | :$$y_{\rm CK}(t) = y_1(t)+y_2(t)+y_3(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})-{\rm | ||
e}^{\hspace{0.05cm}-2 | e}^{\hspace{0.05cm}-2 | ||
| Line 221: | Line 228: | ||
e}^{\hspace{0.05cm}-0.4}} { {1 + \pi^2 | e}^{\hspace{0.05cm}-0.4}} { {1 + \pi^2 | ||
}} \hspace{0.15cm}\underline{ \approx 0.24} < 0.303\hspace{0.05cm} .$$ | }} \hspace{0.15cm}\underline{ \approx 0.24} < 0.303\hspace{0.05cm} .$$ | ||
| − | : | + | :For comparison: The signal $y_{\rm C}(t)$ has the value $0.303$ at this time. |
| − | * | + | * In contrast to this, the following arises as a result in general and specifically at the time of the first maximum at $t = 0.45 \cdot T$ for the causal sinusoidal signal applied to the input: |
:$$y_{\rm SK}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})+\pi \cdot {\rm | :$$y_{\rm SK}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})+\pi \cdot {\rm | ||
e}^{\hspace{0.05cm}-2 | e}^{\hspace{0.05cm}-2 | ||
| Line 237: | Line 244: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^3.3 Inverse Laplace Transform^]] |
Latest revision as of 17:22, 9 December 2021
In this exercise, we consider a cosine signal $c(t)$ with amplitude $1$ and period $T = 1 \ \rm µ s$, which is defined for all times $t$ $($in the range $ \pm \infty)$ :
- $$c(t) = \cos(2\pi \cdot {t}/{T}) \hspace{0.05cm} .$$
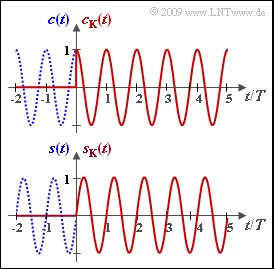
The causal $($German: "kausal" ⇒ subscript "K"$)$ cosine signal $c_{\rm K}(t)$ (red curve) starts only at the turn-on instant $t = 0$:
- $$c_{\rm K}(t)= \left\{ \begin{array}{c} c(t) \\ 0 \end{array} \right. \begin{array}{c} {\rm{for}} \\ {\rm{for}} \end{array}\begin{array}{*{20}c} { t \ge 0\hspace{0.05cm},} \\ { t < 0\hspace{0.05cm}.} \end{array}$$
Only the Fourier spectrum can be specified for the bilaterally unbounded signal $c(t)$:
- $$C(f) = {1}/{ 2} \cdot \delta (f - f_0) + {1}/{ 2} \cdot \delta (f + f_0) \quad {\rm with} \quad f_0 = {1}/{ T}= 1\,\,{\rm MHz.}$$
On the contrary, for the causal cosine signal $c_{\rm K}(t)$ the Laplace transform can also be specified:
- $$C_{\rm L}(p) = \frac {p} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$
Accordingly, the following holds for the Laplace transform of the causal sine function $s_{\rm K}(t)$:
- $$S_{\rm L}(p) = \frac {2 \pi/T} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$
The bilaterally unbounded sine function is denoted by $s(t)$ and is shown as a blue–dotted curve in the below diagram.
The signals $c(t)$, $c_{\rm K}(t)$, $s(t)$ and $s_{\rm K}(t)$ are applied to the input of a low-pass filter of first-order with the following transfer function (or impulse response):
- $$H_{\rm L}(p) = \frac {2 /T} { p + 2 /T} \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad h(t) = {2}/{T} \cdot {\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 \hspace{0.03cm}t/T}.$$
- The corresponding output signals are denoted by $y_{\rm C}(t)$, $y_{\rm CK}(t)$, $y_{\rm S}(t)$ and $y_{\rm SK}(t)$ .
- These signals are to be computed and correlated to each other in this exercise.
Please note:
- The exercise belongs to the chapter Inverse Laplace Transform.
- The computations for subtask (6) are bulky.
- For computing the signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$, for example the residue theorem can be used.
Questions
Solution
- $$H(f) = \frac {2 /T} { {\rm j} \cdot 2 \pi f + 2 /T}= \frac {f_0} { {\rm j} \cdot \pi f + f_0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(f= f_0) = \frac {1} { 1 + {\rm j} \cdot \pi }$$
- $$\Rightarrow \hspace{0.3cm} |H(f= f_0)| = \frac {1} { \sqrt{1 + \pi^2 }} \hspace{0.15cm}\underline{= 0.303}\hspace{0.05cm},\hspace{0.2cm}a(f= f_0)= - {\rm ln}\,\, |H(f= f_0)| \hspace{0.15cm}\underline{\approx 1.194\,\,{\rm Np}}$$
- $$\Rightarrow \hspace{0.3cm} {\rm arc}\,H(f= f_0)= - {\rm arctan}\,(\pi) \hspace{0.15cm}\underline{\approx -72^\circ} \hspace{0.05cm}, \hspace{0.2cm}b(f= f_0)= -{\rm arc}\,H(f= f_0) \hspace{0.15cm}\underline{\approx +72^\circ} \hspace{0.05cm}.$$
(2) The output signal $y_{\rm C}(t)$ is attenuated by the factor $0.303$ and delayed by $\tau \approx 72/360 \cdot T = T/5$ compared to the input signal $c(t)$ .
- Thus, this signal can also be described as follows:
- $$y_{\rm C}(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= 0.303 \cdot \cos(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm C}(t=0) = \frac {1} { {1 + \pi^2 }} \hspace{0.15cm}\underline{\approx 0.092} \hspace{0.05cm}.$$
- This signal is shown dotted in blue in the left graph for solution (5).
(3) The signal $y_{\rm S}(t)$ is also smaller by the attenuation factor $0.303$ and delayed by the time period $\tau = T/5$ compared to $s(t)$ .
- It can be described as follows:
- $$y_{\rm S}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= 0.303 \cdot \sin(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm S}(t=0) = -\frac {\pi} { {1 + \pi^2 }} \hspace{0.15cm}\underline{\approx -0.289} \hspace{0.05cm}.$$
- This signal is sketched dotted in blue in the right graph for solution (5) .
(4) At $T_h$ the impulse response $h(t)$ should have decayed to $1\%$ of the maximum value. Thus, the following holds:
- $${\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 \hspace{0.03cm}T_{ h}/T} = 0.01 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {T_{ h}}/{T} =\frac{1}{2} \cdot {\rm ln}\,\, \frac{1}{0.01} \hspace{0.15cm}\underline{\approx 2.3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}h(t=0) = {2}/{T}\hspace{0.05cm}, \hspace{0.2cm}h(t=T_{ h}) = {0.02}/{T}\hspace{0.05cm}.$$
(5) The statements 1 and 2 are correct:
- The causal signals $y_{\rm CK}(t)$ and $y_{\rm SK}(t)$ must be identical to zero for $t < 0$ .
- However, since the impulse response $h(t)$ of the considered filter (nearly) vanishes for $t > T_h$, it does not matter whether the unbounded cosine signal $c(t)$ or the causal signal $c_{\rm K}(t)$ is applied to the input after the transient effect is over.
- The same is true for the sinusoidal signals: For $t >T_{ h}$, $y_{\rm SK}(t)=y_{\rm S}(t)$ holds.
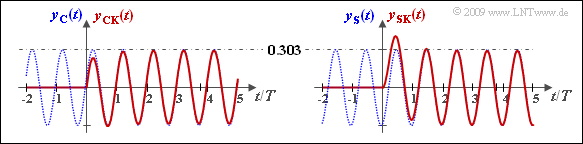
The graph shows the output signals $y_{\rm C}(t)$ and $y_{\rm CK}(t)$ for cosine-shaped input on the left and the signals $y_{\rm S}(t)$ and $y_{\rm SK}(t)$ for sinusoidal input on the right. Note the transit time of $T/5$ $($corresponding to the phase $72^\circ)$ in both cases.
- For $y_{\rm CK}(t)$ the first wave peaks are smaller than $1$ to achieve the correct phase position of $y_{\rm C}(t)$ .
- In contrast, for $y_{\rm SK}(t)$ the first wave peaks are greater than $1$ to achieve the correct phase position of $y_{\rm S}(t)$ .
(6) Considering $p_{\rm x1}= {\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm}p_{\rm x2}= -{\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm} p_{\rm x3}= -{2}/{T} \hspace{0.05cm}$ the following can be written for the Laplace transform of the signal $y_{\rm CK}(t)$ :
- $$Y_{\rm L}(p) = \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})(p-p_{{\rm x}3})} \hspace{0.05cm}.$$
The time function $y_{\rm CK}(t)$ is thus composed of three parts according to the residue theorem:
- Considering $p_{\rm x2}= -p_{\rm x1}$ the first part is
- $$y_1(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}2})(p-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= \frac {-p_{{\rm x}3}\cdot p_{{\rm x}1}} { (p_{{\rm x}1}-p_{{\rm x}2})(p_{{\rm x}1}-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}1}\cdot \hspace{0.03cm}t}= \frac {-p_{{\rm x}3}/2} { p_{{\rm x}1}-p_{{\rm x}3}}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}1}\cdot \hspace{0.03cm}t} \hspace{0.05cm} .$$
- Similarly, the following is obtained for the second part:
- $$y_2(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}=\frac {-p_{{\rm x}3}\cdot p_{{\rm x}2}} { (p_{{\rm x}2}-p_{{\rm x}1})(p_{{\rm x}2}-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}2}\cdot \hspace{0.03cm}t}= \frac {p_{{\rm x}3}/2} { p_{{\rm x}1}+p_{{\rm x}3}}\cdot {\rm e}^{-p_{{\rm x}1}\cdot \hspace{0.03cm}t} \hspace{0.05cm} .$$
- Combining both parts and considering the numerical values of $p_{\rm x1}$ and $p_{\rm x3}$:
- $$y_{1\hspace{0.03cm}+2}(t)= \frac {1/T} { 2/T + {\rm j} \cdot 2\pi /T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm} t/T}+\frac {1/T} { 2/T - {\rm j} \cdot 2\pi /T} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}= \frac {1/2} { 1 + {\rm j} \cdot \pi } \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}+\frac {1/2} { 1 - {\rm j} \cdot \pi } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}$$
- $$\Rightarrow \hspace{0.3cm} y_{1\hspace{0.03cm}+2}(t)\hspace{0.25cm} = \frac {1/2 \cdot (1 - {\rm j} \cdot \pi)} { 1 + \pi^2 } \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}+\frac {1/2 \cdot (1 + {\rm j} \cdot \pi)} { 1 + \pi^2 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T} \hspace{0.05cm} $$
- Using Euler's theorem this can also be expressed as follows:
- $$y_{1\hspace{-0.03cm}+2} (t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= y_{\rm C}(t)\hspace{0.05cm}.$$
- It can be seen that $y_{1\hspace{0.03cm}+2}(t)$ is equal to the signal $y_{\rm C}(t)$ computed in subtask (2) .
- Finally, the following is obtained for the last residual:
- $$y_3(t)=\frac {-p_{{\rm x}3}^2} { (p_{{\rm x}3}-p_{{\rm x}1}) (p_{{\rm x}3}-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}3}\cdot \hspace{0.03cm}t}= \frac {-(2/T)^2 \cdot {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { (-2/T-{\rm j} \cdot 2\pi /T) (-2/T+{\rm j} \cdot 2\pi /T)} =\frac {- {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T} } { (1+{\rm j} \cdot \pi ) (1-{\rm j} \cdot \pi)} =\frac {- {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { 1+\pi^2} \hspace{0.05cm} .$$
- Thus, the output signal is as follows for a causal cosine signal applied to the input:
- $$y_{\rm CK}(t) = y_1(t)+y_2(t)+y_3(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})-{\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { {1 + \pi^2 }}$$
- $$\Rightarrow \hspace{0.3cm}y_{\rm CK}(t = {T}/{5}) = \frac { \cos(72^\circ) + \pi \cdot \sin(72^\circ)-{\rm e}^{\hspace{0.05cm}-0.4}} { {1 + \pi^2 }} \hspace{0.15cm}\underline{ \approx 0.24} < 0.303\hspace{0.05cm} .$$
- For comparison: The signal $y_{\rm C}(t)$ has the value $0.303$ at this time.
- In contrast to this, the following arises as a result in general and specifically at the time of the first maximum at $t = 0.45 \cdot T$ for the causal sinusoidal signal applied to the input:
- $$y_{\rm SK}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})+\pi \cdot {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { {1 + \pi^2 }}$$
- $$\Rightarrow \hspace{0.3cm} y_{\rm SK}(t = 0.45 \cdot T) = \frac { -\pi \cdot \cos(162^\circ) + \sin(162^\circ)+\pi \cdot{\rm e}^{\hspace{0.05cm}-0.9}} { {1 + \pi^2 }} \approx 0.42 > 0.303\hspace{0.05cm} .$$