Difference between revisions of "Aufgaben:Exercise 4.5: Irrelevance Theorem"
m (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| (13 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver}} |
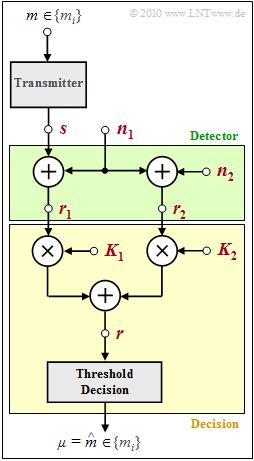
| − | [[File: | + | [[File:EN_Dig_A_4_5.png|right|frame|Considered optimal system with "detector" and "decision"]] |
| − | + | The communication system given by the graph is to be investigated. The binary message $m ∈ \{m_0, m_1\}$ with equal occurrence probabilities | |
:$${\rm Pr} (m_0 ) = {\rm Pr} (m_1 ) = 0.5$$ | :$${\rm Pr} (m_0 ) = {\rm Pr} (m_1 ) = 0.5$$ | ||
| − | + | is represented by the two signals | |
:$$s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$$ | :$$s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$$ | ||
| − | + | where the assignments $m_0 ⇔ s_0$ and $m_1 ⇔ s_1$ are one-to-one. | |
| + | |||
| + | The detector $($highlighted in green in the figure$)$ provides two decision values | ||
:$$r_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s + n_1\hspace{0.05cm},$$ | :$$r_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s + n_1\hspace{0.05cm},$$ | ||
:$$r_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} n_1 + n_2\hspace{0.05cm},$$ | :$$r_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} n_1 + n_2\hspace{0.05cm},$$ | ||
| − | + | from which the decision forms the estimated values $\mu ∈ \{m_0,\ m_1\}$ for the transmitted message $m$. The decision includes | |
| − | * | + | *two weighting factors $K_1$ and $K_2$, |
| − | * | + | |
| − | * | + | *a summation point, and |
| + | |||
| + | *a threshold decision with the threshold at $0$. | ||
| + | |||
| + | |||
| + | Three evaluations are considered in this exercises: | ||
| + | # Decision based on $r_1$ $(K_1 ≠ 0,\ K_2 = 0)$, | ||
| + | # decision based on $r_2$ $(K_1 = 0,\ K_2 ≠ 0)$, | ||
| + | # joint evaluation of $r_1$ und $r_2$ $(K_1 ≠ 0,\ K_2 ≠ 0)$. | ||
| + | |||
| + | |||
| + | <u>Notes:</u> | ||
| + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver|"Structure of the Optimal Receiver"]] of this book. | ||
| − | + | * In particular, [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#The_irrelevance_theorem|"the irrelevance theorem"]] is referred to here, but besides that also the [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#Optimal_receiver_for_the_AWGN_channel|"Optimal receiver for the AWGN channel"]]. | |
| − | * | + | |
| − | * | + | * For more information on topics relevant to this exercise, see the following links: |
| − | * | + | ** [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#Fundamental_approach_to_optimal_receiver_design|"Decision rules for MAP and ML receivers"]], |
| + | ** [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#Implementation_aspects|"Realization as correlation receiver or matched filter receiver"]], | ||
| + | ** [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver#Probability_density_function_of_the_received_values|"Conditional Gaussian probability density functions"]]. | ||
| + | * For the error probability of a system $r = s + n$ $($because of $N = 1$ here $s,\ n,\ r$ are scalars$)$ is valid: | ||
| + | ::$$p_{\rm S} = {\rm Pr} ({\rm symbol\ \ error} ) = {\rm Q} \left ( \sqrt{{2 E_s}/{N_0}}\right ) \hspace{0.05cm},$$ | ||
| − | + | :where a binary message signal $s ∈ \{s_0,\ s_1\}$ with $s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$ is assumed. | |
| + | *Let the two noise sources $n_1$ and $n_2$ be independent of each other and also independent of the transmitted signal $s ∈ \{s_0,\ s_1\}$. | ||
| + | |||
| + | *$n_1$ and $n_2$ can each be modeled by AWGN noise sources $($white, Gaussian distributed, mean-free, variance $\sigma^2 = N_0/2)$. | ||
| + | |||
| + | *For numerical calculations, use the values | ||
:$$E_s = 8 \cdot 10^{-6}\,{\rm Ws}\hspace{0.05cm},\hspace{0.2cm}N_0 = 10^{-6}\,{\rm W/Hz} \hspace{0.05cm}.$$ | :$$E_s = 8 \cdot 10^{-6}\,{\rm Ws}\hspace{0.05cm},\hspace{0.2cm}N_0 = 10^{-6}\,{\rm W/Hz} \hspace{0.05cm}.$$ | ||
| − | + | *The [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Exceedance_probability|"complementary Gaussian error function"]] gives the following results: | |
:$${\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{1.35cm}{\rm Q}(2^{0.5}) = 0.786 \cdot 10^{-1}\hspace{0.05cm},\hspace{1.1cm}{\rm Q}(2) = 0.227 \cdot 10^{-1}\hspace{0.05cm},$$ | :$${\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{1.35cm}{\rm Q}(2^{0.5}) = 0.786 \cdot 10^{-1}\hspace{0.05cm},\hspace{1.1cm}{\rm Q}(2) = 0.227 \cdot 10^{-1}\hspace{0.05cm},$$ | ||
:$${\rm Q}(2 \cdot 2^{0.5}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.234 \cdot 10^{-2}\hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4) = 0.317 \cdot 10^{-4} | :$${\rm Q}(2 \cdot 2^{0.5}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.234 \cdot 10^{-2}\hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4) = 0.317 \cdot 10^{-4} | ||
| Line 35: | Line 58: | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements apply here regarding the receiver? |
|type="()"} | |type="()"} | ||
| − | - | + | - The ML receiver is better than the MAP receiver. |
| − | - | + | - The MAP receiver is better than the ML receiver. |
| − | + | + | + Both receivers deliver the same result. |
| − | { | + | {What is the error probability with $K_2 = 0$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr( | + | ${\rm Pr(symbol\hspace{0.15cm} error)}\ = \ $ { 0.00317 3% } $\ \%$ |
| − | { | + | {What is the error probability with $K_1 = 0$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr( | + | ${\rm Pr(symbol\hspace{0.15cm}error)}\ = \ $ { 50 3% } $\ \%$ |
| − | { | + | {Can an improvement be achieved by using $r_1$ <b>and</b> $r_2$? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {What are the equations for the estimated value $(\mu)$ for AWGN noise? |
|type="[]"} | |type="[]"} | ||
| − | - $\mu = {\rm arg \ min} \, [(\rho_1 + \rho_2) \cdot s_i]$, | + | - $\mu = {\rm arg \ min} \, \big[(\rho_1 + \rho_2) \cdot s_i \big]$, |
| − | + $\mu = {\rm arg \ min} \, [(\rho_2 \, - 2 \rho_1) \cdot s_i]$, | + | + $\mu = {\rm arg \ min} \, \big[(\rho_2 \, - 2 \rho_1) \cdot s_i \big]$, |
| − | + $\mu = {\rm arg \ max} \, [(\rho_1 - \rho_2/2) \cdot s_i]$. | + | + $\mu = {\rm arg \ max} \, \big[(\rho_1 - \rho_2/2) \cdot s_i \big]$. |
| − | { | + | {How can this rule be implemented exactly with the given decision (threshold at zero)? Let $K_1 = 1$. |
|type="{}"} | |type="{}"} | ||
$K_2 \ = \ $ { -0.515--0.485 } | $K_2 \ = \ $ { -0.515--0.485 } | ||
| − | { | + | {What is the (minimum) error probability with the realization according to subtask '''(6)'''? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Minimum \ [Pr( | + | ${\rm Minimum \ \big[Pr(symbol\hspace{0.15cm}error)\big]} \ = \ $ { 0.771 3% } $\ \cdot 10^{\rm -8}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The <u>last alternative solution</u> is correct: |
| − | * | + | *In general, the MAP receiver leads to a smaller error probability. |
| − | * | + | *However, if the occurrence probabilities ${\rm Pr}(m = m_0) = {\rm Pr}(m = m_1) = 0.5$ are equal, both receivers yield the same result. |
| − | '''(2)''' | + | '''(2)''' With $K_2 = 0$ and $K_1 = 1$ the result is |
:$$r = r_1 = s + n_1\hspace{0.05cm}.$$ | :$$r = r_1 = s + n_1\hspace{0.05cm}.$$ | ||
| − | + | *With bipolar (antipodal) transmitted signal and AWGN noise, the error probability of the optimal receiver (whether implemented as a correlation or matched filter receiver) is equal to | |
| − | :$$p_{\rm S} = {\rm Pr} ({\rm | + | :$$p_{\rm S} = {\rm Pr} ({\rm symbol\hspace{0.15cm} error} ) = {\rm Q} \left ( \sqrt{ E_s /{\sigma}}\right ) |
= {\rm Q} \left ( \sqrt{2 E_s /N_0}\right ) \hspace{0.05cm}.$$ | = {\rm Q} \left ( \sqrt{2 E_s /N_0}\right ) \hspace{0.05cm}.$$ | ||
| − | + | *With $E_s = 8 \cdot 10^{\rm –6} \ \rm Ws$ and $N_0 = 10^{\rm –6} \ \rm W/Hz$, we further obtain: | |
| − | :$$p_{\rm S} = {\rm Pr} ({\rm | + | :$$p_{\rm S} = {\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Q} \left ( \sqrt{\frac{2 \cdot 8 \cdot 10^{-6}\,{\rm Ws}}{10^{-6}\,{\rm W/Hz} }}\right ) = {\rm Q} (4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.00317 \%}\hspace{0.05cm}.$$ |
| − | + | *This result is independent of $K_1$, since amplification or attenuation changes the useful power in the same way as the noise power. | |
| − | '''(3)''' | + | '''(3)''' With $K_1 = 0$ and $K_2 = 1$, the decision variable is: |
:$$r = r_2 = n_1 + n_2\hspace{0.05cm}.$$ | :$$r = r_2 = n_1 + n_2\hspace{0.05cm}.$$ | ||
| − | + | *This contains no information about the useful signal, only noise, and it holds independently of $K_2$: | |
| − | :$$p_{\rm S} = {\rm Pr} ({\rm | + | :$$p_{\rm S} = {\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Q} (0) \hspace{0.15cm}\underline {= 50\%} \hspace{0.05cm}.$$ |
| − | '''(4)''' | + | '''(4)''' Because of ${\rm Pr}(m = m_0) = {\rm Pr}(m = m_1)$, the decision rule of the optimal receiver (whether realized as MAP or as ML) is: |
:$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ p_{m \hspace{0.05cm}|\hspace{0.05cm}r_1, \hspace{0.05cm}r_2 } \hspace{0.05cm} (m_i \hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}\rho_2 ) ] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} m} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} m_i ) \cdot {\rm Pr} (m = m_i)] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} s_i ) ] | :$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ p_{m \hspace{0.05cm}|\hspace{0.05cm}r_1, \hspace{0.05cm}r_2 } \hspace{0.05cm} (m_i \hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}\rho_2 ) ] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} m} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} m_i ) \cdot {\rm Pr} (m = m_i)] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} s_i ) ] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *This composite probability density can be rewritten as follows: | |
:$$\hat{m} ={\rm arg} \max_i \hspace{0.1cm} [ p_{r_1 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1 \hspace{0.05cm}|\hspace{0.05cm} s_i ) \cdot p_{r_2 \hspace{0.05cm}|\hspace{0.05cm} r_1, \hspace{0.05cm}s} \hspace{0.05cm} ( \rho_2 \hspace{0.05cm}|\hspace{0.05cm} \rho_1, \hspace{0.05cm}s_i ) ] | :$$\hat{m} ={\rm arg} \max_i \hspace{0.1cm} [ p_{r_1 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1 \hspace{0.05cm}|\hspace{0.05cm} s_i ) \cdot p_{r_2 \hspace{0.05cm}|\hspace{0.05cm} r_1, \hspace{0.05cm}s} \hspace{0.05cm} ( \rho_2 \hspace{0.05cm}|\hspace{0.05cm} \rho_1, \hspace{0.05cm}s_i ) ] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Now, since the second multiplicand also depends on the message ($s_i$), $r_2$ should definitely be included in the decision process. Thus, the correct answer is: <u>YES</u>. | |
| − | '''(5)''' | + | '''(5)''' For AWGN noise with variance $\sigma^2$, the two composite densities introduced in '''(4)''' together with their product $P$ give: |
:$$p_{r_1\hspace{0.05cm}|\hspace{0.05cm} s}(\rho_1\hspace{0.05cm}|\hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_1 - s_i)^2}{2 \sigma^2}\right ]\hspace{0.05cm},\hspace{1cm} | :$$p_{r_1\hspace{0.05cm}|\hspace{0.05cm} s}(\rho_1\hspace{0.05cm}|\hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_1 - s_i)^2}{2 \sigma^2}\right ]\hspace{0.05cm},\hspace{1cm} | ||
p_{r_2\hspace{0.05cm}|\hspace{0.05cm}r_1,\hspace{0.05cm} s}(\rho_2\hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_2 - (\rho_1 - s_i))^2}{2 \sigma^2}\right ]\hspace{0.05cm}$$ | p_{r_2\hspace{0.05cm}|\hspace{0.05cm}r_1,\hspace{0.05cm} s}(\rho_2\hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_2 - (\rho_1 - s_i))^2}{2 \sigma^2}\right ]\hspace{0.05cm}$$ | ||
| Line 134: | Line 143: | ||
+ (\rho_2 - (\rho_1 - s_i))^2\right \}\right ]\hspace{0.05cm}.$$ | + (\rho_2 - (\rho_1 - s_i))^2\right \}\right ]\hspace{0.05cm}.$$ | ||
| − | + | *We are looking for the argument that maximizes this product $P$, which at the same time means that the expression in the curly brackets should take the smallest possible value: | |
:$$\mu = \hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm arg} \max_i \hspace{0.1cm} P = {\rm arg} \min _i \hspace{0.1cm} \left \{ (\rho_1 - s_i)^2 | :$$\mu = \hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm arg} \max_i \hspace{0.1cm} P = {\rm arg} \min _i \hspace{0.1cm} \left \{ (\rho_1 - s_i)^2 | ||
+ (\rho_2 - (\rho_1 - s_i))^2\right \} $$ | + (\rho_2 - (\rho_1 - s_i))^2\right \} $$ | ||
| Line 141: | Line 150: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Here $\mu$ denotes the estimated value of the message. In this minimization, all terms that do not depend on the message $s_i$ can now be omitted. Likewise, the terms $s_i^2$ are disregarded, since $s_0^2 = s_1^2$ holds. Thus, the much simpler decision rule is obtained: | |
:$$\mu = {\rm arg} \min _i \hspace{0.1cm}\left \{ - 4\rho_1 s_i + 2\rho_2 s_i \right \}={\rm arg} \min _i \hspace{0.1cm}\left \{ (\rho_2 - 2\rho_1) \cdot s_i \right \} | :$$\mu = {\rm arg} \min _i \hspace{0.1cm}\left \{ - 4\rho_1 s_i + 2\rho_2 s_i \right \}={\rm arg} \min _i \hspace{0.1cm}\left \{ (\rho_2 - 2\rho_1) \cdot s_i \right \} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *So, correct is already the proposed solution 2. But after multiplication by $–1/2$, we also get the last mentioned decision rule: | |
:$$\mu = {\rm arg} \max_i \hspace{0.1cm}\left \{ (\rho_1 - \rho_2/2) \cdot s_i \right \} | :$$\mu = {\rm arg} \max_i \hspace{0.1cm}\left \{ (\rho_1 - \rho_2/2) \cdot s_i \right \} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Thus, the <u>solutions 2 and 3</u> are correct. | |
| − | '''(6)''' | + | '''(6)''' Setting $K_1 = 1$ and $\underline {K_2 = \, -0.5}$, the optimal decision rule with realization $\rho = \rho_1 \, – \rho_2/2$ is: |
:$$\mu = | :$$\mu = | ||
\left\{ \begin{array}{c} m_0 \\ | \left\{ \begin{array}{c} m_0 \\ | ||
m_1 \end{array} \right.\quad | m_1 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm f{ | + | \begin{array}{*{1}c} {\rm f{or}} \hspace{0.15cm} \rho > 0 \hspace{0.05cm}, |
| − | \\ {\rm f{ | + | \\ {\rm f{or}} \hspace{0.15cm} \rho < 0 \hspace{0.05cm}.\\ \end{array}$$ |
| − | + | *Since $\rho = 0$ only occurs with probability $0$, it does not matter in the sense of probability theory whether one assigns the message $\mu = m_0$ or $\mu = m_1$ to this event "$\rho = 0$". | |
| − | '''(7)''' | + | '''(7)''' With $K_2 = \, -0.5$ one obtains for the input value of the decision: |
:$$r = r_1 - r_2/2 = s + n_1 - (n_1 + n_2)/2 = s + n \hspace{0.3cm} | :$$r = r_1 - r_2/2 = s + n_1 - (n_1 + n_2)/2 = s + n \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} n = \frac{n_1 - n_2}{2}\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm} n = \frac{n_1 - n_2}{2}\hspace{0.05cm}.$$ | ||
| − | + | *The variance of this random variable is | |
:$$\sigma_n^2 = {1}/{4} \cdot \left [ \sigma^2 + \sigma^2 \right ] = {\sigma^2}/{2}= {N_0}/{4}\hspace{0.05cm}.$$ | :$$\sigma_n^2 = {1}/{4} \cdot \left [ \sigma^2 + \sigma^2 \right ] = {\sigma^2}/{2}= {N_0}/{4}\hspace{0.05cm}.$$ | ||
| − | + | *From this, the error probability is analogous to subtask '''(2)''': | |
| − | :$${\rm Pr} ({\rm | + | :$${\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Q} \left ( \sqrt{\frac{E_s}{N_0/4}}\right ) = |
{\rm Q} \left ( 4 \cdot \sqrt{2}\right ) = {1}/{2} \cdot {\rm erfc}(4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}} | {\rm Q} \left ( 4 \cdot \sqrt{2}\right ) = {1}/{2} \cdot {\rm erfc}(4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, by taking $r_2$ into account, the error probability can be lowered from $0.317 \cdot 10^{\rm –4}$ to the much smaller value of $0.771 \cdot 10^{-8}$, although the decision component $r_2$ contains only noise. However, this noise $r_2$ allows an estimate of the noise component $n_1$ of $r_1$. |
| − | * | + | *Halving the transmit energy from $8 \cdot 10^{\rm –6} \ \rm Ws$ to $4 \cdot 10^{\rm –6} \ \rm Ws$, we still get the error probability $0.317 \cdot 10^{\rm –4}$ here, as calculated in subtask '''(2)'''. When evaluating $r_1$ alone, on the other hand, the error probability would be $0.234 \cdot 10^{\rm –2}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.2 Structure of the Optimal Receiver^]] |
Latest revision as of 12:38, 18 July 2022
The communication system given by the graph is to be investigated. The binary message $m ∈ \{m_0, m_1\}$ with equal occurrence probabilities
- $${\rm Pr} (m_0 ) = {\rm Pr} (m_1 ) = 0.5$$
is represented by the two signals
- $$s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$$
where the assignments $m_0 ⇔ s_0$ and $m_1 ⇔ s_1$ are one-to-one.
The detector $($highlighted in green in the figure$)$ provides two decision values
- $$r_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s + n_1\hspace{0.05cm},$$
- $$r_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} n_1 + n_2\hspace{0.05cm},$$
from which the decision forms the estimated values $\mu ∈ \{m_0,\ m_1\}$ for the transmitted message $m$. The decision includes
- two weighting factors $K_1$ and $K_2$,
- a summation point, and
- a threshold decision with the threshold at $0$.
Three evaluations are considered in this exercises:
- Decision based on $r_1$ $(K_1 ≠ 0,\ K_2 = 0)$,
- decision based on $r_2$ $(K_1 = 0,\ K_2 ≠ 0)$,
- joint evaluation of $r_1$ und $r_2$ $(K_1 ≠ 0,\ K_2 ≠ 0)$.
Notes:
- The exercise belongs to the chapter "Structure of the Optimal Receiver" of this book.
- In particular, "the irrelevance theorem" is referred to here, but besides that also the "Optimal receiver for the AWGN channel".
- For more information on topics relevant to this exercise, see the following links:
- For the error probability of a system $r = s + n$ $($because of $N = 1$ here $s,\ n,\ r$ are scalars$)$ is valid:
- $$p_{\rm S} = {\rm Pr} ({\rm symbol\ \ error} ) = {\rm Q} \left ( \sqrt{{2 E_s}/{N_0}}\right ) \hspace{0.05cm},$$
- where a binary message signal $s ∈ \{s_0,\ s_1\}$ with $s_0 = \sqrt{E_s} \hspace{0.05cm},\hspace{0.2cm}s_1 = -\sqrt{E_s}$ is assumed.
- Let the two noise sources $n_1$ and $n_2$ be independent of each other and also independent of the transmitted signal $s ∈ \{s_0,\ s_1\}$.
- $n_1$ and $n_2$ can each be modeled by AWGN noise sources $($white, Gaussian distributed, mean-free, variance $\sigma^2 = N_0/2)$.
- For numerical calculations, use the values
- $$E_s = 8 \cdot 10^{-6}\,{\rm Ws}\hspace{0.05cm},\hspace{0.2cm}N_0 = 10^{-6}\,{\rm W/Hz} \hspace{0.05cm}.$$
- The "complementary Gaussian error function" gives the following results:
- $${\rm Q}(0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5\hspace{0.05cm},\hspace{1.35cm}{\rm Q}(2^{0.5}) = 0.786 \cdot 10^{-1}\hspace{0.05cm},\hspace{1.1cm}{\rm Q}(2) = 0.227 \cdot 10^{-1}\hspace{0.05cm},$$
- $${\rm Q}(2 \cdot 2^{0.5}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.234 \cdot 10^{-2}\hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4) = 0.317 \cdot 10^{-4} \hspace{0.05cm},\hspace{0.2cm}{\rm Q}(4 \cdot 2^{0.5}) = 0.771 \cdot 10^{-8}\hspace{0.05cm}.$$
Questions
Solution
- In general, the MAP receiver leads to a smaller error probability.
- However, if the occurrence probabilities ${\rm Pr}(m = m_0) = {\rm Pr}(m = m_1) = 0.5$ are equal, both receivers yield the same result.
(2) With $K_2 = 0$ and $K_1 = 1$ the result is
- $$r = r_1 = s + n_1\hspace{0.05cm}.$$
- With bipolar (antipodal) transmitted signal and AWGN noise, the error probability of the optimal receiver (whether implemented as a correlation or matched filter receiver) is equal to
- $$p_{\rm S} = {\rm Pr} ({\rm symbol\hspace{0.15cm} error} ) = {\rm Q} \left ( \sqrt{ E_s /{\sigma}}\right ) = {\rm Q} \left ( \sqrt{2 E_s /N_0}\right ) \hspace{0.05cm}.$$
- With $E_s = 8 \cdot 10^{\rm –6} \ \rm Ws$ and $N_0 = 10^{\rm –6} \ \rm W/Hz$, we further obtain:
- $$p_{\rm S} = {\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Q} \left ( \sqrt{\frac{2 \cdot 8 \cdot 10^{-6}\,{\rm Ws}}{10^{-6}\,{\rm W/Hz} }}\right ) = {\rm Q} (4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.00317 \%}\hspace{0.05cm}.$$
- This result is independent of $K_1$, since amplification or attenuation changes the useful power in the same way as the noise power.
(3) With $K_1 = 0$ and $K_2 = 1$, the decision variable is:
- $$r = r_2 = n_1 + n_2\hspace{0.05cm}.$$
- This contains no information about the useful signal, only noise, and it holds independently of $K_2$:
- $$p_{\rm S} = {\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Q} (0) \hspace{0.15cm}\underline {= 50\%} \hspace{0.05cm}.$$
(4) Because of ${\rm Pr}(m = m_0) = {\rm Pr}(m = m_1)$, the decision rule of the optimal receiver (whether realized as MAP or as ML) is:
- $$\hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm arg} \max_i \hspace{0.1cm} [ p_{m \hspace{0.05cm}|\hspace{0.05cm}r_1, \hspace{0.05cm}r_2 } \hspace{0.05cm} (m_i \hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}\rho_2 ) ] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} m} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} m_i ) \cdot {\rm Pr} (m = m_i)] = {\rm arg} \max_i \hspace{0.1cm} [ p_{r_1, \hspace{0.05cm}r_2 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1, \hspace{0.05cm}\rho_2 \hspace{0.05cm}|\hspace{0.05cm} s_i ) ] \hspace{0.05cm}.$$
- This composite probability density can be rewritten as follows:
- $$\hat{m} ={\rm arg} \max_i \hspace{0.1cm} [ p_{r_1 \hspace{0.05cm}|\hspace{0.05cm} s} \hspace{0.05cm} ( \rho_1 \hspace{0.05cm}|\hspace{0.05cm} s_i ) \cdot p_{r_2 \hspace{0.05cm}|\hspace{0.05cm} r_1, \hspace{0.05cm}s} \hspace{0.05cm} ( \rho_2 \hspace{0.05cm}|\hspace{0.05cm} \rho_1, \hspace{0.05cm}s_i ) ] \hspace{0.05cm}.$$
- Now, since the second multiplicand also depends on the message ($s_i$), $r_2$ should definitely be included in the decision process. Thus, the correct answer is: YES.
(5) For AWGN noise with variance $\sigma^2$, the two composite densities introduced in (4) together with their product $P$ give:
- $$p_{r_1\hspace{0.05cm}|\hspace{0.05cm} s}(\rho_1\hspace{0.05cm}|\hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_1 - s_i)^2}{2 \sigma^2}\right ]\hspace{0.05cm},\hspace{1cm} p_{r_2\hspace{0.05cm}|\hspace{0.05cm}r_1,\hspace{0.05cm} s}(\rho_2\hspace{0.05cm}|\hspace{0.05cm}\rho_1, \hspace{0.05cm}s_i) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi} \cdot \sigma}\cdot {\rm exp} \left [ - \frac{(\rho_2 - (\rho_1 - s_i))^2}{2 \sigma^2}\right ]\hspace{0.05cm}$$
- $$ \Rightarrow \hspace{0.3cm} P \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{{2\pi} \cdot \sigma^2}\cdot {\rm exp} \left [ - \frac{1}{2 \sigma^2} \cdot \left \{ (\rho_1 - s_i)^2 + (\rho_2 - (\rho_1 - s_i))^2\right \}\right ]\hspace{0.05cm}.$$
- We are looking for the argument that maximizes this product $P$, which at the same time means that the expression in the curly brackets should take the smallest possible value:
- $$\mu = \hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm arg} \max_i \hspace{0.1cm} P = {\rm arg} \min _i \hspace{0.1cm} \left \{ (\rho_1 - s_i)^2 + (\rho_2 - (\rho_1 - s_i))^2\right \} $$
- $$\Rightarrow \hspace{0.3cm} \mu = \hat{m} \hspace{-0.1cm} \ = \ \hspace{-0.1cm}{\rm arg} \min _i \hspace{0.1cm}\left \{ \rho_1^2 - 2\rho_1 s_i + s_i^2 + \rho_2^2 - 2\rho_1 \rho_2 + 2\rho_2 s_i+ \rho_1^2 - 2\rho_1 s_i + s_i^2\right \} \hspace{0.05cm}.$$
- Here $\mu$ denotes the estimated value of the message. In this minimization, all terms that do not depend on the message $s_i$ can now be omitted. Likewise, the terms $s_i^2$ are disregarded, since $s_0^2 = s_1^2$ holds. Thus, the much simpler decision rule is obtained:
- $$\mu = {\rm arg} \min _i \hspace{0.1cm}\left \{ - 4\rho_1 s_i + 2\rho_2 s_i \right \}={\rm arg} \min _i \hspace{0.1cm}\left \{ (\rho_2 - 2\rho_1) \cdot s_i \right \} \hspace{0.05cm}.$$
- So, correct is already the proposed solution 2. But after multiplication by $–1/2$, we also get the last mentioned decision rule:
- $$\mu = {\rm arg} \max_i \hspace{0.1cm}\left \{ (\rho_1 - \rho_2/2) \cdot s_i \right \} \hspace{0.05cm}.$$
- Thus, the solutions 2 and 3 are correct.
(6) Setting $K_1 = 1$ and $\underline {K_2 = \, -0.5}$, the optimal decision rule with realization $\rho = \rho_1 \, – \rho_2/2$ is:
- $$\mu = \left\{ \begin{array}{c} m_0 \\ m_1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f{or}} \hspace{0.15cm} \rho > 0 \hspace{0.05cm}, \\ {\rm f{or}} \hspace{0.15cm} \rho < 0 \hspace{0.05cm}.\\ \end{array}$$
- Since $\rho = 0$ only occurs with probability $0$, it does not matter in the sense of probability theory whether one assigns the message $\mu = m_0$ or $\mu = m_1$ to this event "$\rho = 0$".
(7) With $K_2 = \, -0.5$ one obtains for the input value of the decision:
- $$r = r_1 - r_2/2 = s + n_1 - (n_1 + n_2)/2 = s + n \hspace{0.3cm} \Rightarrow \hspace{0.3cm} n = \frac{n_1 - n_2}{2}\hspace{0.05cm}.$$
- The variance of this random variable is
- $$\sigma_n^2 = {1}/{4} \cdot \left [ \sigma^2 + \sigma^2 \right ] = {\sigma^2}/{2}= {N_0}/{4}\hspace{0.05cm}.$$
- From this, the error probability is analogous to subtask (2):
- $${\rm Pr} ({\rm symbol\hspace{0.15cm}error} ) = {\rm Q} \left ( \sqrt{\frac{E_s}{N_0/4}}\right ) = {\rm Q} \left ( 4 \cdot \sqrt{2}\right ) = {1}/{2} \cdot {\rm erfc}(4) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.771 \cdot 10^{-8}} \hspace{0.05cm}.$$
- Thus, by taking $r_2$ into account, the error probability can be lowered from $0.317 \cdot 10^{\rm –4}$ to the much smaller value of $0.771 \cdot 10^{-8}$, although the decision component $r_2$ contains only noise. However, this noise $r_2$ allows an estimate of the noise component $n_1$ of $r_1$.
- Halving the transmit energy from $8 \cdot 10^{\rm –6} \ \rm Ws$ to $4 \cdot 10^{\rm –6} \ \rm Ws$, we still get the error probability $0.317 \cdot 10^{\rm –4}$ here, as calculated in subtask (2). When evaluating $r_1$ alone, on the other hand, the error probability would be $0.234 \cdot 10^{\rm –2}$.