Difference between revisions of "Aufgaben:Exercise 4.6: Quantization Characteristics"
From LNTwww
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Pulse_Code_Modulation |
}} | }} | ||
| − | [[File: | + | [[File:EN_Mod_A_4_6_neu.png|right|frame|Non-linear quantization characteristics]] |
| − | + | Non-linear quantization is considered. The system model according to [[Aufgaben:Exercise_4.5:_Non-Linear_Quantization| Exercise 4.5]] still applies. | |
| − | |||
| − | |||
| − | |||
| + | The graph shows two compressor characteristics $q_{\rm K}(q_{\rm A})$: | ||
| + | * Drawn in red is the so-called "'''A-characteristic'''" recommended by the CCITT ("Comité Consultatif International Téléphonique et Télégraphique") for the standard system PCM 30/32. For $0 ≤ q_{\rm A} ≤ 1$ applies here: | ||
| + | :$$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} {{1}/{A} \le q_{\rm A} \le 1} \hspace{0.05cm}, \\ \\ {q_{\rm A} < {1}/{A}} \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | * The blue-dashed curve applies to the so-called "'''13-segment characteristic'''". This is obtained from the A-characteristic by piecewise linearization; it is treated in detail in the [[Aufgaben:Exercise_4.5:_Non-Linear_Quantization| Exercise 4.5]] . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | Hints: | ||
| + | *The Exercise belongs to the chapter [[Modulation_Methods/Pulse_Code_Modulation|"Pulse Code Modulation"]]. | ||
| + | *Reference is made in particular to the page [[Modulation_Methods/Pulse_Code_Modulation#Compression_and_expansion|"Compression and Expansion"]]. | ||
| + | *For the A-characteristic drawn in solid red, the quantization parameter $A = 100$ is chosen. With the value $A = 87.56$ suggested by CCITT, a similar curve is obtained. | ||
| + | *For the other two curves, | ||
| + | :* $A = A_1$ (dash–dotted curve) and | ||
| + | :* $A = A_2$ (dotted curve), | ||
| + | |||
| + | where for $A_1$ and $A_2$ the two possible numerical values $50$ and $200$ are given. In the subtask '''(3)''' you are to decide which curve belongs to which numerical value. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the arguments for non-linear quantization? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The larger SNR – even with equally likely amplitudes. |
| − | + | + | + For audio, small amplitudes are more likely than large ones. |
| − | + | + | + The distortion of small amplitudes is subjectively more disturbing. |
| − | { | + | {What are the differences between the "A-characteristic" and the "13-segment characteristic"? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The A-characteristic curve describes a continuous course. |
| − | + | + | + The 13-segment curve approximates the A-characteristic linearly piece by piece. |
| − | - | + | - In the realization, the A-characteristic shows significant advantages. |
| − | { | + | {Can the parameter $A$ be derived from $q_{\rm A} = 1$ ⇒ $q_{\rm K} = 1$ alone? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Yes. |
| − | + | + | + No. |
| − | { | + | {Can the parameter $A$ be determined if we specify that the transition between the two domains should be continuous? |
| − | |type=" | + | |type="()"} |
| − | - | + | - Yes. |
| − | + | + | + No. |
| − | { | + | {Determine the parameter $A$ from the condition $q_{\rm K}(q_{\rm A} = 1/2) = 0.8756$. |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 94 3% } | $A \ = \ $ { 94 3% } | ||
| − | { | + | {What parameter values were used for the other curves? |
| − | |type=" | + | |type="()"} |
| − | - | + | - It holds $A_1 = 50$ and $A_2 = 200$. |
| − | + | + | + It holds $A_1 = 200$ and $A_2 = 50$. |
| − | |||
| Line 60: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>statements 2 and 3</u>: |
| − | * | + | *Signal distortion of soft sounds or in speech pauses is subjectively perceived as more disturbing than e.g. additional noise in heavy metal. |
| − | * | + | *In terms of quantization noise or SNR, however, there is no improvement due to non-linear quantization if an uniformly distribution of the amplitude values is assumed. |
| − | * | + | *However, if one considers that in speech and music signals smaller amplitudes occur much more frequently than large ⇒ "Laplace distribution", non-linear quantization also results in a better SNR. |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Correct are the <u>statements 1 and 2</u>: | ||
| + | *Due to the linearization in the individual segments, the interval width of the various quantization levels is constant in these for the "13-segment characteristic", which has a favorable effect in realization. | ||
| + | *In contrast, with the non-linear quantization according to the "A-characteristic", there are no quantization intervals of equal width. <br>This means: The statement 3 is false. | ||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' Correct is "<u>NO</u>": | ||
| + | *For $q_{\rm A} = 1$ one obtains independently of $A$ the value $q_{\rm K} = 1$. | ||
| + | *So with this specification alone $A$ cannot be determined. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' Correct is again "<u>NO</u>": | ||
| + | *For $q_{\rm A} = 1/A$ both range equations yield the same value $q_{\rm K}= 1/[1 + \ln(A)]$. | ||
| + | *Also with this $A$ cannot be determined. | ||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' | + | '''(5)''' With this requirement $A$ is now computable: |
:$$0.875 = \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A/2)} {1 | :$$0.875 = \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A/2)} {1 | ||
\hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} = | \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} = | ||
| Line 96: | Line 109: | ||
94} \hspace{0.05cm}.$$ | 94} \hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | |
| − | * | + | |
| − | * | + | '''(6)''' Correct is <u>statement 2</u>: |
| + | *The curve for $A_1 = 200$ lies above the curve with $A = 100$, the curve with $A_2 = 50$ below. | ||
| + | *This is shown by the following calculation for $q_{\rm A} = 0.5$: | ||
:$$A= 100\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1 + \ln(100) - \ln(2)}{1 + \ln(100)}= | :$$A= 100\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1 + \ln(100) - \ln(2)}{1 + \ln(100)}= | ||
\frac{1+4.605- 0.693} {1 +4.605}\approx | \frac{1+4.605- 0.693} {1 +4.605}\approx | ||
| − | 0.876 | + | 0.876 \hspace{0.05cm},$$ |
:$$A= 200\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1+5.298- 0.693} {1 +5.298}\approx | :$$A= 200\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1+5.298- 0.693} {1 +5.298}\approx | ||
| − | 0.890 | + | 0.890 \hspace{0.05cm},$$ |
:$$A= 50\text{:}\hspace{0.4cm} q_{\rm K}= \frac{1+3.912- 0.693} {1 +3.912}\approx | :$$A= 50\text{:}\hspace{0.4cm} q_{\rm K}= \frac{1+3.912- 0.693} {1 +3.912}\approx | ||
| − | 0.859 | + | 0.859 \hspace{0.05cm}.$$ |
| Line 115: | Line 130: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.1 Pulse Code Modulation^]] |
Latest revision as of 15:01, 11 April 2022
Non-linear quantization is considered. The system model according to Exercise 4.5 still applies.
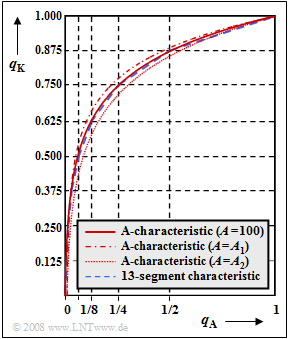
The graph shows two compressor characteristics $q_{\rm K}(q_{\rm A})$:
- Drawn in red is the so-called "A-characteristic" recommended by the CCITT ("Comité Consultatif International Téléphonique et Télégraphique") for the standard system PCM 30/32. For $0 ≤ q_{\rm A} ≤ 1$ applies here:
- $$q_{\rm K}(q_{\rm A}) = \left\{ \begin{array}{l} \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A})} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \\ \frac{A \hspace{0.05cm}\cdot \hspace{0.05cm}q_{\rm A}} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} \\ \end{array} \right.\quad \begin{array}{*{10}c} {{1}/{A} \le q_{\rm A} \le 1} \hspace{0.05cm}, \\ \\ {q_{\rm A} < {1}/{A}} \hspace{0.05cm}. \\ \end{array}$$
- The blue-dashed curve applies to the so-called "13-segment characteristic". This is obtained from the A-characteristic by piecewise linearization; it is treated in detail in the Exercise 4.5 .
Hints:
- The Exercise belongs to the chapter "Pulse Code Modulation".
- Reference is made in particular to the page "Compression and Expansion".
- For the A-characteristic drawn in solid red, the quantization parameter $A = 100$ is chosen. With the value $A = 87.56$ suggested by CCITT, a similar curve is obtained.
- For the other two curves,
- $A = A_1$ (dash–dotted curve) and
- $A = A_2$ (dotted curve),
where for $A_1$ and $A_2$ the two possible numerical values $50$ and $200$ are given. In the subtask (3) you are to decide which curve belongs to which numerical value.
Questions
Solution
(1) Correct are the statements 2 and 3:
- Signal distortion of soft sounds or in speech pauses is subjectively perceived as more disturbing than e.g. additional noise in heavy metal.
- In terms of quantization noise or SNR, however, there is no improvement due to non-linear quantization if an uniformly distribution of the amplitude values is assumed.
- However, if one considers that in speech and music signals smaller amplitudes occur much more frequently than large ⇒ "Laplace distribution", non-linear quantization also results in a better SNR.
(2) Correct are the statements 1 and 2:
- Due to the linearization in the individual segments, the interval width of the various quantization levels is constant in these for the "13-segment characteristic", which has a favorable effect in realization.
- In contrast, with the non-linear quantization according to the "A-characteristic", there are no quantization intervals of equal width.
This means: The statement 3 is false.
(3) Correct is "NO":
- For $q_{\rm A} = 1$ one obtains independently of $A$ the value $q_{\rm K} = 1$.
- So with this specification alone $A$ cannot be determined.
(4) Correct is again "NO":
- For $q_{\rm A} = 1/A$ both range equations yield the same value $q_{\rm K}= 1/[1 + \ln(A)]$.
- Also with this $A$ cannot be determined.
(5) With this requirement $A$ is now computable:
- $$0.875 = \frac{1 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A/2)} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )} = \frac{1\hspace{0.05cm}-\hspace{0.05cm} {\rm ln}(2) \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A)} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )}\approx \frac{1-0.693 \hspace{0.05cm}+\hspace{0.05cm} {\rm ln}(A)} {1 \hspace{0.05cm}+ \hspace{0.05cm}{\rm ln}(A )}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm ln}(A) = \frac{0.875 - 0.307 } {1 -0.875 }= 4.544 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A \hspace{0.15cm}\underline {\approx 94} \hspace{0.05cm}.$$
(6) Correct is statement 2:
- The curve for $A_1 = 200$ lies above the curve with $A = 100$, the curve with $A_2 = 50$ below.
- This is shown by the following calculation for $q_{\rm A} = 0.5$:
- $$A= 100\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1 + \ln(100) - \ln(2)}{1 + \ln(100)}= \frac{1+4.605- 0.693} {1 +4.605}\approx 0.876 \hspace{0.05cm},$$
- $$A= 200\text{:}\hspace{0.2cm} q_{\rm K}= \frac{1+5.298- 0.693} {1 +5.298}\approx 0.890 \hspace{0.05cm},$$
- $$A= 50\text{:}\hspace{0.4cm} q_{\rm K}= \frac{1+3.912- 0.693} {1 +3.912}\approx 0.859 \hspace{0.05cm}.$$