Difference between revisions of "Aufgaben:Exercise 5.3: Mean Square Error"
| (22 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Possible_Errors_When_Using_DFT |
}} | }} | ||
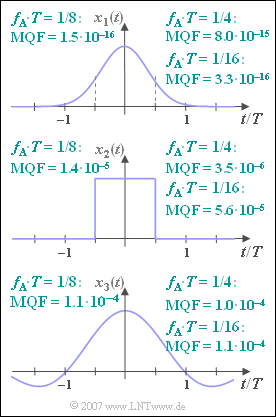
| − | [[File:P_ID1145__Sig_A_5_3.png|250px|right|frame| | + | [[File:P_ID1145__Sig_A_5_3.png|250px|right|frame|Gaussian pulse, square pulse, <br>sinc pulse and some parameters]] |
| − | + | We consider three pulses, namely | |
| − | * | + | *a [[Signal_Representation/Special_Cases_of_Pulses#Gaussian_pulse|Gaussian pulse]] with amplitude $A$ and equivalent duration $T$: |
:$$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$ | :$$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$ | ||
| − | * | + | *a [[Signal_Representation/Special_Cases_of_Pulses#Rectangular_pulse|rectangular pulse]] $x_2(t)$ with amplitude $A$ and (equivalent) duration $T$: |
:$$x_2(t) = \left\{ \begin{array}{c} A \\ | :$$x_2(t) = \left\{ \begin{array}{c} A \\ | ||
| Line 20: | Line 20: | ||
\end{array}$$ | \end{array}$$ | ||
| − | * | + | *a so called "sinc pulse" according to the following definition: |
| − | :$$x_3(t) = A \cdot {\rm | + | :$$x_3(t) = A \cdot {\rm sinc}(t/ T) ,\hspace{0.15cm}{\rm sinc}(x) = |
| − | \sin(x)/x\hspace{0.05cm}.$$ | + | \sin(\pi x)/(\pi x)\hspace{0.05cm}.$$ |
| − | + | Let the signal parameters be $A = 1\ {\rm V}$ and $T = 1\ {\rm ms}$ in each case. | |
| − | + | The conventional [[Signal_Representation/Fourier_Transform_and_Its_Inverse|Fourier transform]] leads to the following spectral functions: | |
| − | * $X_1(f)$ | + | * $X_1(f)$ is also Gaussian, |
| − | * $X_2(f)$ | + | * $X_2(f)$ runs according to the $\rm sinc$ function, |
| − | * $X_3(f)$ | + | * $X_3(f)$ is constant for $|f| < 1/(2 T)$ and outside zero. |
| − | + | For all spectral functions, $X(f = 0) = A \cdot T$. | |
| − | + | If the discrete-frequency spectrum is determined by the [[Signal_Representation/Discrete_Fourier_Transform_(DFT)|Discrete Fourier Transform]] $\rm (DFT)$ with the DFT parameters | |
| − | * $N = 512$ ⇒ | + | * $N = 512$ ⇒ number of samples considered in the time and frequency domain, |
| − | *$f_{\rm A}$ ⇒ | + | *$f_{\rm A}$ ⇒ interpolation distance in the frequency domain, |
| − | + | this will lead to distortions due to truncation and/or aliasing errors. | |
| − | + | ||
| − | + | The other DFT parameters are clearly fixed withn $N$ and $f_{\rm A}$. The following applies to these: | |
:$$f_{\rm P} = N \cdot f_{\rm A},\hspace{0.3cm}T_{\rm P} = 1/f_{\rm A},\hspace{0.3cm}T_{\rm A} = T_{\rm | :$$f_{\rm P} = N \cdot f_{\rm A},\hspace{0.3cm}T_{\rm P} = 1/f_{\rm A},\hspace{0.3cm}T_{\rm A} = T_{\rm | ||
P}/N | P}/N | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The accuracy of the respective DFT approximation is captured by the "mean square error" $\rm (MSE)$. <br>Here, we use the designation $\rm MQF$ ⇒ (German: "Mittlerer Quadratischer Fehler"): | |
| − | |||
:$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | :$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | ||
\left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | ||
| − | + | The resulting MQF values are given in the graph above, valid for $N = 512$ as well as for | |
*$f_{\rm A} \cdot T = 1/4$, | *$f_{\rm A} \cdot T = 1/4$, | ||
*$f_{\rm A} \cdot T = 1/8$, | *$f_{\rm A} \cdot T = 1/8$, | ||
| Line 62: | Line 61: | ||
| − | '' | + | |
| − | * | + | |
| + | |||
| + | ''Hints:'' | ||
| + | *This task belongs to the chapter [[Signal_Representation/Possible_Errors_When_Using_DFT|Possible errors when using DFT]]. | ||
| − | * | + | *The theory for this chapter is summarised in the (German language) learning video <br> [[Fehlermöglichkeiten_bei_Anwendung_der_DFT_(Lernvideo)|Fehlermöglichkeiten bei Anwendung der DFT]] ⇒ "Possible errors when using DFT". |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which range $|f| \leq f_{\text{max}}$ is covered with $N = 512$ and $f_{\rm A} \cdot T = 1/8$ ? |
|type="{}"} | |type="{}"} | ||
$f_{\text{max}} \cdot T\ = \ $ { 32 3% } | $f_{\text{max}} \cdot T\ = \ $ { 32 3% } | ||
| − | { | + | {At what time interval $T_{\rm A}$ are the sampled values of $x(t)$ available? |
|type="{}"} | |type="{}"} | ||
$T_{\rm A}/T\ = \ $ { 0.01562 3% } | $T_{\rm A}/T\ = \ $ { 0.01562 3% } | ||
| − | { | + | {Due to which effect does the MQF value for the Gaussian pulse increase when using $f_{\rm A} \cdot T = 1/4$ instead of $f_{\rm A} \cdot T = 1/8$? |
| − | |type=" | + | |type="()"} |
| − | + | + | + The truncation error is significantly increased. |
| − | - | + | - The aliasing error is significantly increased. |
| − | { | + | {Due to what effect does the MQF value for the Gaussian pulse increase when using $f_{\rm A} \cdot T = 1/16$ instead of $f_{\rm A} \cdot T = 1/4$? |
| − | |type=" | + | |type="()"} |
| − | - | + | - The truncation error is significantly increased. |
| − | + | + | + The aliasing error is significantly increased. |
| − | { | + | {Compare the $\rm MQF$ values of the rectangular pulse $x_2(t)$ with those of the Gaussian pulse $x_1(t)$. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + $\rm MQF$ | + | + $\rm MQF$ becomes larger because the spectral function $X_2(f)$ decays asymptotically slower than $X_1(f)$. |
| − | + | + | + The aliasing error dominates. |
| − | - | + | - The truncation error dominates. |
| − | { | + | {Compare the $\rm MQF$ values of the "sinc pulse" $x_3(t)$ with those of the Gaussian pulse $x_1(t)$. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - $\rm MQF$ | + | - $\rm MQF$ becomes larger because the spectral function $X_3(f)$ decays asymptotically slower than $X_1(f)$. |
| − | - | + | - The aliasing error dominates. |
| − | + | + | + The truncation error dominates. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With the DFT parameters $N = 512$ and $f_{\rm A} \cdot T = 1/8$ the following follows after multiplying the two quantities: |
:$$f_{\rm P} \cdot T = N \cdot (f_{\rm A} \cdot T) = 64.$$ | :$$f_{\rm P} \cdot T = N \cdot (f_{\rm A} \cdot T) = 64.$$ | ||
| − | + | *This covers the frequency range $-f_{\rm P}/2 \leq f < +f_{\rm P}/2$: | |
:$$f_{\rm max }\cdot T \hspace{0.15 cm}\underline{= 32}\hspace{0.05cm}.$$ | :$$f_{\rm max }\cdot T \hspace{0.15 cm}\underline{= 32}\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | |
| + | '''(2)''' The periodisation of the time function is based on the parameter $T_{\rm P} = 1/f_{\rm A} = 8T$. | ||
| + | *The distance between two samples is therefore | ||
:$$T_{\rm A}/T = \frac{T_{\rm P}/T}{N} = \frac{8}{512}\hspace{0.15 cm}\underline{ = 0.015625}\hspace{0.05cm}.$$ | :$$T_{\rm A}/T = \frac{T_{\rm P}/T}{N} = \frac{8}{512}\hspace{0.15 cm}\underline{ = 0.015625}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| − | * | + | '''(3)''' Correct is the <u>proposed solution 1 ⇒ increase of the truncation error</u>: |
| − | * | + | *This measure simultaneously halves $T_{\rm P}$ from $8T$ to $4T$ . |
| − | * | + | *Thus, only samples in the range $–2T \leq t < 2T$ are taken into account, which increases the truncation error. |
| + | *The mean square error $(\rm MQF)$ increases from $0.15 \cdot 10^{-15}$ to $8 \cdot 10^{-15}$ for the Gaussian pulse $x_1(t)$, | ||
| + | *although the aliasing error actually decreases slightly by this measure. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Correct is the <u>proposed solution 2 ⇒ increase of the aliasing error:</u>: | ||
| + | *By halving $f_{\rm A}$ ⇒ $f_{\rm P}$ is also halved. | ||
| + | *As a result, the aliasing error becomes somewhat larger with a smaller truncation error at the same time. | ||
| + | *Overall, for the Gaussian pulse $x_1(t)$, the mean square error $(\rm MQF)$ increases from $1.5 \cdot 10^{-16}$ to $3.3 \cdot 10^{-16}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(5)''' <u>Proposed solutions 1 and 2</u> are correct: | ||
| + | *As can be seen from the graph, the last statement is not true in contrast to the first two. | ||
| + | *Due to the slow ($\rm sinc$–shaped) decay of the spectral function, the aliasing error dominates. | ||
| + | *The $\rm MQF$ value at $f_{\rm A} \cdot T = 1/8$ with $1.4 \cdot 10^{-5}$ is therefore significantly larger than for the Gaussian pulse $(1.5 \cdot 10^{-16})$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(6)''' | + | '''(6)''' <u>Proposed solution 3</u> is correct: |
| − | * | + | *The spectral function $X_3(f)$ here has a rectangular lead, so that the first two statements do not apply. |
| − | * | + | *On the other hand, a truncation error is unavoidable with this $\rm sinc$–shaped time function. This leads to the large $\rm MQF$ values given. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^5.3 Possible DFT Errors^]] |
Latest revision as of 16:14, 17 May 2021
We consider three pulses, namely
- a Gaussian pulse with amplitude $A$ and equivalent duration $T$:
- $$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$
- a rectangular pulse $x_2(t)$ with amplitude $A$ and (equivalent) duration $T$:
- $$x_2(t) = \left\{ \begin{array}{c} A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \hspace{0.05cm}, \\ \end{array}$$
- a so called "sinc pulse" according to the following definition:
- $$x_3(t) = A \cdot {\rm sinc}(t/ T) ,\hspace{0.15cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x)\hspace{0.05cm}.$$
Let the signal parameters be $A = 1\ {\rm V}$ and $T = 1\ {\rm ms}$ in each case.
The conventional Fourier transform leads to the following spectral functions:
- $X_1(f)$ is also Gaussian,
- $X_2(f)$ runs according to the $\rm sinc$ function,
- $X_3(f)$ is constant for $|f| < 1/(2 T)$ and outside zero.
For all spectral functions, $X(f = 0) = A \cdot T$.
If the discrete-frequency spectrum is determined by the Discrete Fourier Transform $\rm (DFT)$ with the DFT parameters
- $N = 512$ ⇒ number of samples considered in the time and frequency domain,
- $f_{\rm A}$ ⇒ interpolation distance in the frequency domain,
this will lead to distortions due to truncation and/or aliasing errors.
The other DFT parameters are clearly fixed withn $N$ and $f_{\rm A}$. The following applies to these:
- $$f_{\rm P} = N \cdot f_{\rm A},\hspace{0.3cm}T_{\rm P} = 1/f_{\rm A},\hspace{0.3cm}T_{\rm A} = T_{\rm P}/N \hspace{0.05cm}.$$
The accuracy of the respective DFT approximation is captured by the "mean square error" $\rm (MSE)$.
Here, we use the designation $\rm MQF$ ⇒ (German: "Mittlerer Quadratischer Fehler"):
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
The resulting MQF values are given in the graph above, valid for $N = 512$ as well as for
- $f_{\rm A} \cdot T = 1/4$,
- $f_{\rm A} \cdot T = 1/8$,
- $f_{\rm A} \cdot T = 1/16$.
Hints:
- This task belongs to the chapter Possible errors when using DFT.
- The theory for this chapter is summarised in the (German language) learning video
Fehlermöglichkeiten bei Anwendung der DFT ⇒ "Possible errors when using DFT".
Questions
Solution
- $$f_{\rm P} \cdot T = N \cdot (f_{\rm A} \cdot T) = 64.$$
- This covers the frequency range $-f_{\rm P}/2 \leq f < +f_{\rm P}/2$:
- $$f_{\rm max }\cdot T \hspace{0.15 cm}\underline{= 32}\hspace{0.05cm}.$$
(2) The periodisation of the time function is based on the parameter $T_{\rm P} = 1/f_{\rm A} = 8T$.
- The distance between two samples is therefore
- $$T_{\rm A}/T = \frac{T_{\rm P}/T}{N} = \frac{8}{512}\hspace{0.15 cm}\underline{ = 0.015625}\hspace{0.05cm}.$$
(3) Correct is the proposed solution 1 ⇒ increase of the truncation error:
- This measure simultaneously halves $T_{\rm P}$ from $8T$ to $4T$ .
- Thus, only samples in the range $–2T \leq t < 2T$ are taken into account, which increases the truncation error.
- The mean square error $(\rm MQF)$ increases from $0.15 \cdot 10^{-15}$ to $8 \cdot 10^{-15}$ for the Gaussian pulse $x_1(t)$,
- although the aliasing error actually decreases slightly by this measure.
(4) Correct is the proposed solution 2 ⇒ increase of the aliasing error::
- By halving $f_{\rm A}$ ⇒ $f_{\rm P}$ is also halved.
- As a result, the aliasing error becomes somewhat larger with a smaller truncation error at the same time.
- Overall, for the Gaussian pulse $x_1(t)$, the mean square error $(\rm MQF)$ increases from $1.5 \cdot 10^{-16}$ to $3.3 \cdot 10^{-16}$.
(5) Proposed solutions 1 and 2 are correct:
- As can be seen from the graph, the last statement is not true in contrast to the first two.
- Due to the slow ($\rm sinc$–shaped) decay of the spectral function, the aliasing error dominates.
- The $\rm MQF$ value at $f_{\rm A} \cdot T = 1/8$ with $1.4 \cdot 10^{-5}$ is therefore significantly larger than for the Gaussian pulse $(1.5 \cdot 10^{-16})$.
(6) Proposed solution 3 is correct:
- The spectral function $X_3(f)$ here has a rectangular lead, so that the first two statements do not apply.
- On the other hand, a truncation error is unavoidable with this $\rm sinc$–shaped time function. This leads to the large $\rm MQF$ values given.