Difference between revisions of "Aufgaben:Exercise 4.14Z: Echo Detection"
From LNTwww
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Cross-Correlation_Function_and_Cross_Power_Density |
}} | }} | ||
| − | [[File: | + | [[File:EN_Sto_Z_4_14.png|right|Echo measuring arrangement|frame]] |
| − | + | To measure acoustic echoes in rooms – for example caused by reflections at a wall – the adjacent setup can be used: | |
| − | * | + | *The noise generator produces a "white noise in the relevant frequency range" $x(t)$ with power density $N_0 = 10^{-6} \hspace{0.08cm} \rm W/Hz$. |
| − | * | + | *This is bandlimited to $B_x = 20 \hspace{0.08cm} \rm kHz$ and is given to a loudspeaker. |
| − | * | + | *The entire measurement setup is designed for the resistance value $R = 50 \hspace{0.08cm} \rm \Omega$. |
| − | + | In the most general case, the signal recorded by the microphone can be described as follows: | |
:$$y(t) = \sum_{\mu = 1}^M \alpha_\mu \cdot x ( t - t_\mu ) .$$ | :$$y(t) = \sum_{\mu = 1}^M \alpha_\mu \cdot x ( t - t_\mu ) .$$ | ||
| − | + | Here the $\alpha_\mu$ denote damping factors and $t_\mu$ delay times. | |
| − | + | Hints: | |
| − | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Cross-Correlation_Function_and_Cross_Power_Density|Cross-Correlation Function and Cross Power-Spectral Density]]. | |
| − | * | ||
| − | * | + | *Use for numerical calculations the parameter values. |
:$$\alpha_1 = 0.5, \hspace{0.2cm}t_1 = 200 \,{\rm ms}, \hspace{0.2cm} \alpha_2 = 0.1, \hspace{0.2cm}t_2 = 250 \,{\rm ms}.$$ | :$$\alpha_1 = 0.5, \hspace{0.2cm}t_1 = 200 \,{\rm ms}, \hspace{0.2cm} \alpha_2 = 0.1, \hspace{0.2cm}t_2 = 250 \,{\rm ms}.$$ | ||
| Line 29: | Line 28: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Apply the $\rm ACF$ $\varphi_x(\tau)$ at the transmitter. What means this converted to the resistor $R = 50 \hspace{0.08cm} \rm \Omega$ ? What is the rms value $\sigma_x$ ? |
|type="{}"} | |type="{}"} | ||
$\sigma_x \ = \ $ { 1 3% } $\ \rm V$ | $\sigma_x \ = \ $ { 1 3% } $\ \rm V$ | ||
| − | { | + | {Calculate the cross-correlation function $\rm (CCF)$ $\varphi_{xy}(\tau)$ between transmitted and received signal. <br>What values result for $\tau = 0$, $\tau = t_1 = 200 \hspace{0.08cm} \rm ms$ and $\tau = t_2 = 250 \hspace{0.08cm} \rm ms$ ? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_{xy}(\tau= 0) \ = | + | $\varphi_{xy}(\tau= 0) \ = \ $ { 0. } $\ \rm V^2$ |
| − | $\varphi_{xy}(\tau= t_1) \ = | + | $\varphi_{xy}(\tau= t_1) \ = \ $ { 0.5 3% } $\ \rm V^2$ |
| − | $\varphi_{xy}(\tau= t_2) \ = | + | $\varphi_{xy}(\tau= t_2) \ = \ $ { 0.1 3% } $\ \rm V^2$ |
| − | { | + | {Calculate the cross power-spectral density ${\it \Phi}_{xy}(f)$. What value is obtained at frequency $f = 0$? |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_{xy}(f =0)\ = | + | ${\it \Phi}_{xy}(f =0)\ = \ $ { 15 3% } $\ \cdot 10^{-6}\ \rm V^2\hspace{-0.1cm}/Hz$ |
| − | { | + | {Which of the following statements are true if you use the approximation $\varphi_{x}(\tau) \approx N_0/2 \cdot \delta(\tau)$ instead of the ACF calculated in '''(1)'''? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The noise is now "true white" – so it is not bandlimited. |
| − | - | + | - The noise power is reduced compared to subtask '''(1)'''. |
| − | + | + | + The cross-correlation function is the sum of weighted and shifted Dirac delta functions. |
| − | - | + | - The cross power-spectral density is calculated as in subtask '''(3)'''. |
| − | { | + | {Calculate the $\rm ACF$ $\varphi_y(\tau)$ using the approximation $\varphi_{xy}(\tau) \approx N_0/2 \cdot \delta(\tau)$. What weights result for $\tau = 0$ and $\tau = \Delta t = t_2 - t_1$? |
|type="{}"} | |type="{}"} | ||
| − | $\varphi_{y}(\tau= 0) \ = | + | $\varphi_{y}(\tau= 0) \ = \ $ { 0.13 3% } $\ \cdot 10^{-6}\ \rm W\hspace{-0.1cm}/Hz$ |
| − | $\varphi_{y}(\tau= \Delta t) \ = | + | $\varphi_{y}(\tau= \Delta t) \ = \ $ { 0.025 3% } $\ \cdot 10^{-6}\ \rm W\hspace{-0.1cm}/Hz$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The two-sided power-spectral density ${\it \Phi}_{x}(f)$ is constantly equal $N_0/2$ in the range $\pm B_x$. |
| − | :$$\varphi_x (\tau) = {N_0}/{2} \cdot 2 B_x \cdot {\rm | + | *The Fourier transform is the ACF: |
| + | :$$\varphi_x (\tau) = {N_0}/{2} \cdot 2 B_x \cdot {\rm sinc} (2 B_x \tau) = 0.02 \hspace {0.08cm}{\rm W} \cdot {\rm sinc} (2 B_x \tau).$$ | ||
| − | + | *Converted from $R = 50 \hspace{0.08cm} \rm \Omega$ to $R = 1 \hspace{0.08cm} \rm \Omega$ one obtains $($multiplication by $R = 50 \hspace{0.08cm} \rm \Omega)$: | |
| − | :$$\varphi_x (\tau) = | + | :$$\varphi_x (\tau) = 0.02 \hspace {0.05cm}{\rm VA} \cdot 50 \hspace {0.05cm}{\rm V/A}\cdot {\rm sinc} (2 B_x \tau)= 1 \hspace {0.05cm}{\rm V}^2 \cdot {\rm sinc} (2 B_x \tau).$$ |
| − | + | *The rms value is the square root of the ACF value at $\tau = 0$: | |
| + | :$$\sigma_x \hspace{0.15cm}\underline{= 1 \hspace {0.08cm}{\rm V}}.$$ | ||
| − | '''(2)''' | + | '''(2)''' For the cross correlation function (CCF), in the present case: |
| − | :$$\varphi_{xy} (\tau) = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)} = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}\ | + | :$$\varphi_{xy} (\tau) = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)} = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}\big [ \alpha_1 \cdot x(t- t_1+ \tau)\hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot x(t- t_2+ \tau)\big] } . $$ |
| − | + | *After splitting the averaging on two terms, we get: | |
:$$\varphi_{xy} (\tau) = \alpha_1 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_1+ \tau)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_2+ \tau)} .$$ | :$$\varphi_{xy} (\tau) = \alpha_1 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_1+ \tau)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_2+ \tau)} .$$ | ||
| − | + | *Using the ACF $\varphi_x(\tau)$ can also be written: | |
| − | :$$\varphi_{xy} (\tau) = \alpha_1 \cdot {\varphi_{x}(\tau- t_1)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2\cdot {\varphi_{x}(\tau- t_2)} = | + | :$$\varphi_{xy} (\tau) = \alpha_1 \cdot {\varphi_{x}(\tau- t_1)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2\cdot {\varphi_{x}(\tau- t_2)} = 1 \hspace {0.08cm}{\rm V}^2 \cdot \big[ \alpha_1 \cdot {\rm sinc} (2 B_x (\tau - t_1)) + \alpha_2 \cdot {\rm sinc} (2 B_x (\tau - t_2)) \big].$$ |
| − | + | *The sinc–function exhibits equidistant zero crossings at all multiples of $1/(2B_x) = 25 \hspace{0.08cm} µ \rm s$, related to the centers at $t_1 = 200 \hspace{0.08cm} {\rm ms}$ and $t_2 = 250 \hspace{0.08cm} {\rm ms}$. This results in the CCF values: | |
:$$\varphi_{xy} (\tau = 0) \hspace{0.15cm}\underline{= 0},\hspace{0.5cm}\varphi_{xy} (\tau = t_1)= \alpha_1 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.5\,{\rm V}^2} ,\hspace{0.5cm} \varphi_{xy} (\tau = t_2)= \alpha_2 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.1\,{\rm V}^2} .$$ | :$$\varphi_{xy} (\tau = 0) \hspace{0.15cm}\underline{= 0},\hspace{0.5cm}\varphi_{xy} (\tau = t_1)= \alpha_1 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.5\,{\rm V}^2} ,\hspace{0.5cm} \varphi_{xy} (\tau = t_2)= \alpha_2 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.1\,{\rm V}^2} .$$ | ||
| − | '''(3)''' | + | '''(3)''' The cross power-spectral density is the Fourier transform of the CCF, just as the power-spectral density $\rm (PSD)$ gives the Fourier transform of the ACF. It holds: |
| − | :$${\it \Phi}_{xy} (f) = \alpha_1 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ | + | :$${\it \Phi}_{xy} (f) = \alpha_1 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_2}. $$ |
| + | |||
| + | *Outside of the range $|f| \le B_x$ the power-spectral density ${\it \Phi}_{x}(f)$ – and correspondingly the cross power-spectral density ${\it \Phi}_{xy}(f)$ – is identically zero. | ||
| + | *In contrast, inside this interval holds ${\it \Phi}_{x}(f) = N_0/2$. It follows in this range: | ||
| + | [[File:P_ID450__Sto_Z_4_14_d.png|right|frame|ACF and CCF with white noise]] | ||
| + | :$${\it \Phi}_{xy} (f) = {N_0}/{2} \left( \alpha_1 \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\rm e}^{-{\rm j}2 \pi f t_2} \right). $$ | ||
| + | |||
| + | *It is evident that ${\it \Phi}_{xy}(f)$ unlike ${\it \Phi}_{x}(f)$ is a complex function. For $f = 0$ holds: | ||
| + | :$${\it \Phi}_{xy} (f = 0) = {N_0}/{2} \left( \alpha_1 \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \right) = 0.3 \cdot 10^{-6}\hspace{0.05cm}{\rm W/Hz} \hspace{0.15cm}\underline{= 15 \cdot 10^{-6}\hspace{0.07cm}{\rm V^2/Hz}} . $$ | ||
| + | |||
| − | |||
| − | |||
| − | + | '''(4)''' Correct are <u>the proposed solutions 1 and 3</u>: | |
| − | + | *The Fourier transform of a Dirac-shaped ACF leads to a constant PSD for all frequencies $f$ ⇒ "true white noise". | |
| − | :$$ | + | *This has an infinitely large power, and for the CCF can then be written according to the above graph: |
| + | :$$\varphi_{xy} (\tau) = \alpha_1 \cdot { N_0}/{2} \cdot {\rm \delta}( \tau - t_1) \hspace {0.1cm}+ \hspace {0.1cm} \alpha_2 \cdot { N_0}/{2} \cdot { \rm \delta}( \tau - t_2) .$$ | ||
| + | *In the frequency domain, no difference is detectable for $|f| \le B_x$ compared to subtask '''(3)''' . | ||
| + | *But since "true white noise" is now present, here the cross power-spectral density is not limited to this range. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' | + | '''(5)''' For the ACF of the echoed signal, $\varphi_{y} (\tau) = \overline {y(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)}$. |
| − | :$$\alpha_1^2 \cdot \overline {x(t - t_1) \cdot x(t - t_1+ \tau)} \hspace{0.03cm} + \hspace{0.03cm} \alpha_1\hspace{0.02cm}\alpha_2 \cdot | + | *This ACF $\varphi_{y} (\tau)$ can consequently be represented as the following sum: |
| + | :$$\alpha_1^2 \cdot \overline {x(t - t_1) \cdot x(t - t_1+ \tau)} \hspace{0.03cm} + \hspace{0.03cm} \alpha_1\hspace{0.02cm}\alpha_2 \cdot \overline {x(t - t_1) \cdot x(t - t_2+ \tau)} + \hspace{0.05cm} \alpha_2\hspace{0.02cm}\alpha_1 \cdot \overline {x(t - t_2) \cdot x(t - t_1+ \tau)}\hspace{0.03cm} + \hspace{0.03cm} \alpha_2^2 \cdot \overline {x(t - t_2) \cdot x(t - t_2+ \tau)}. $$ | ||
| − | + | *For the first and the last mean: | |
:$$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + \tau)} =\varphi_x(\tau).$$ | :$$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + \tau)} =\varphi_x(\tau).$$ | ||
| − | + | *In contrast, for the second and third mean values, we obtain with $\Delta t = t_2 - t_1= 50 \ \rm ms$: | |
:$$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_1- t_2+ \tau)} =\varphi_x(\tau - \Delta t),$$ | :$$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_1- t_2+ \tau)} =\varphi_x(\tau - \Delta t),$$ | ||
:$$\overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_2- t_1+ \tau)} =\varphi_x(\tau + \Delta t).$$ | :$$\overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_2- t_1+ \tau)} =\varphi_x(\tau + \Delta t).$$ | ||
| − | + | *Total, this again results in a symmetric ACF, as shown in the graph below: | |
| − | :$$\varphi_{y} (\tau) = {N_0}/{2} \cdot \left[ ( \alpha_1^2 \hspace{0.1cm} + \hspace{0.1cm} | + | :$$\varphi_{y} (\tau) = {N_0}/{2} \cdot \left[ ( \alpha_1^2 \hspace{0.1cm} + \hspace{0.1cm} \alpha_2^2 ) \cdot {\rm \delta} (\tau) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau - \delta t) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau + \Delta t) \right].$$ |
:$$\Rightarrow \hspace{0.3cm}\varphi_{y} (\tau = 0 ) \hspace{0.15cm}\underline{= 0.13 \cdot 10^{-6}\, {\rm W/Hz}}, | :$$\Rightarrow \hspace{0.3cm}\varphi_{y} (\tau = 0 ) \hspace{0.15cm}\underline{= 0.13 \cdot 10^{-6}\, {\rm W/Hz}}, | ||
\hspace{0.3cm}\varphi_{y} (\tau = \Delta t )\hspace{0.15cm}\underline{ = 0.025 \cdot 10^{-6}\, {\rm W/Hz}}.$$ | \hspace{0.3cm}\varphi_{y} (\tau = \Delta t )\hspace{0.15cm}\underline{ = 0.025 \cdot 10^{-6}\, {\rm W/Hz}}.$$ | ||
| Line 123: | Line 131: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^4.6 CCF and Cross Power-Spectral Density^]] |
Latest revision as of 16:51, 10 April 2022
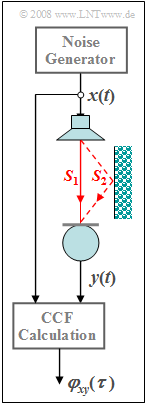
To measure acoustic echoes in rooms – for example caused by reflections at a wall – the adjacent setup can be used:
- The noise generator produces a "white noise in the relevant frequency range" $x(t)$ with power density $N_0 = 10^{-6} \hspace{0.08cm} \rm W/Hz$.
- This is bandlimited to $B_x = 20 \hspace{0.08cm} \rm kHz$ and is given to a loudspeaker.
- The entire measurement setup is designed for the resistance value $R = 50 \hspace{0.08cm} \rm \Omega$.
In the most general case, the signal recorded by the microphone can be described as follows:
- $$y(t) = \sum_{\mu = 1}^M \alpha_\mu \cdot x ( t - t_\mu ) .$$
Here the $\alpha_\mu$ denote damping factors and $t_\mu$ delay times.
Hints:
- The exercise belongs to the chapter Cross-Correlation Function and Cross Power-Spectral Density.
- Use for numerical calculations the parameter values.
- $$\alpha_1 = 0.5, \hspace{0.2cm}t_1 = 200 \,{\rm ms}, \hspace{0.2cm} \alpha_2 = 0.1, \hspace{0.2cm}t_2 = 250 \,{\rm ms}.$$
Questions
Solution
(1) The two-sided power-spectral density ${\it \Phi}_{x}(f)$ is constantly equal $N_0/2$ in the range $\pm B_x$.
- The Fourier transform is the ACF:
- $$\varphi_x (\tau) = {N_0}/{2} \cdot 2 B_x \cdot {\rm sinc} (2 B_x \tau) = 0.02 \hspace {0.08cm}{\rm W} \cdot {\rm sinc} (2 B_x \tau).$$
- Converted from $R = 50 \hspace{0.08cm} \rm \Omega$ to $R = 1 \hspace{0.08cm} \rm \Omega$ one obtains $($multiplication by $R = 50 \hspace{0.08cm} \rm \Omega)$:
- $$\varphi_x (\tau) = 0.02 \hspace {0.05cm}{\rm VA} \cdot 50 \hspace {0.05cm}{\rm V/A}\cdot {\rm sinc} (2 B_x \tau)= 1 \hspace {0.05cm}{\rm V}^2 \cdot {\rm sinc} (2 B_x \tau).$$
- The rms value is the square root of the ACF value at $\tau = 0$:
- $$\sigma_x \hspace{0.15cm}\underline{= 1 \hspace {0.08cm}{\rm V}}.$$
(2) For the cross correlation function (CCF), in the present case:
- $$\varphi_{xy} (\tau) = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)} = \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm}\big [ \alpha_1 \cdot x(t- t_1+ \tau)\hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot x(t- t_2+ \tau)\big] } . $$
- After splitting the averaging on two terms, we get:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_1+ \tau)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2 \cdot \overline {x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} x(t- t_2+ \tau)} .$$
- Using the ACF $\varphi_x(\tau)$ can also be written:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot {\varphi_{x}(\tau- t_1)} \hspace{0.1cm}+\hspace{0.1cm} \alpha_2\cdot {\varphi_{x}(\tau- t_2)} = 1 \hspace {0.08cm}{\rm V}^2 \cdot \big[ \alpha_1 \cdot {\rm sinc} (2 B_x (\tau - t_1)) + \alpha_2 \cdot {\rm sinc} (2 B_x (\tau - t_2)) \big].$$
- The sinc–function exhibits equidistant zero crossings at all multiples of $1/(2B_x) = 25 \hspace{0.08cm} µ \rm s$, related to the centers at $t_1 = 200 \hspace{0.08cm} {\rm ms}$ and $t_2 = 250 \hspace{0.08cm} {\rm ms}$. This results in the CCF values:
- $$\varphi_{xy} (\tau = 0) \hspace{0.15cm}\underline{= 0},\hspace{0.5cm}\varphi_{xy} (\tau = t_1)= \alpha_1 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.5\,{\rm V}^2} ,\hspace{0.5cm} \varphi_{xy} (\tau = t_2)= \alpha_2 \cdot \varphi_{x} (\tau = 0) \hspace{0.15cm}\underline{= 0.1\,{\rm V}^2} .$$
(3) The cross power-spectral density is the Fourier transform of the CCF, just as the power-spectral density $\rm (PSD)$ gives the Fourier transform of the ACF. It holds:
- $${\it \Phi}_{xy} (f) = \alpha_1 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\it \Phi}_{x} (f) \cdot {\rm e}^{-{\rm j}2 \pi f t_2}. $$
- Outside of the range $|f| \le B_x$ the power-spectral density ${\it \Phi}_{x}(f)$ – and correspondingly the cross power-spectral density ${\it \Phi}_{xy}(f)$ – is identically zero.
- In contrast, inside this interval holds ${\it \Phi}_{x}(f) = N_0/2$. It follows in this range:
- $${\it \Phi}_{xy} (f) = {N_0}/{2} \left( \alpha_1 \cdot {\rm e}^{-{\rm j}2 \pi f t_1} \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \cdot {\rm e}^{-{\rm j}2 \pi f t_2} \right). $$
- It is evident that ${\it \Phi}_{xy}(f)$ unlike ${\it \Phi}_{x}(f)$ is a complex function. For $f = 0$ holds:
- $${\it \Phi}_{xy} (f = 0) = {N_0}/{2} \left( \alpha_1 \hspace{0.15cm}+ \hspace{0.15cm}\alpha_2 \right) = 0.3 \cdot 10^{-6}\hspace{0.05cm}{\rm W/Hz} \hspace{0.15cm}\underline{= 15 \cdot 10^{-6}\hspace{0.07cm}{\rm V^2/Hz}} . $$
(4) Correct are the proposed solutions 1 and 3:
- The Fourier transform of a Dirac-shaped ACF leads to a constant PSD for all frequencies $f$ ⇒ "true white noise".
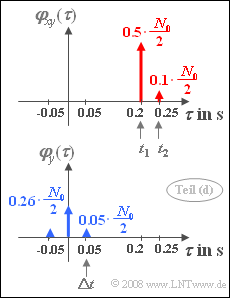
- This has an infinitely large power, and for the CCF can then be written according to the above graph:
- $$\varphi_{xy} (\tau) = \alpha_1 \cdot { N_0}/{2} \cdot {\rm \delta}( \tau - t_1) \hspace {0.1cm}+ \hspace {0.1cm} \alpha_2 \cdot { N_0}/{2} \cdot { \rm \delta}( \tau - t_2) .$$
- In the frequency domain, no difference is detectable for $|f| \le B_x$ compared to subtask (3) .
- But since "true white noise" is now present, here the cross power-spectral density is not limited to this range.
(5) For the ACF of the echoed signal, $\varphi_{y} (\tau) = \overline {y(t) \hspace{0.05cm}\cdot \hspace{0.05cm}y(t+\tau)}$.
- This ACF $\varphi_{y} (\tau)$ can consequently be represented as the following sum:
- $$\alpha_1^2 \cdot \overline {x(t - t_1) \cdot x(t - t_1+ \tau)} \hspace{0.03cm} + \hspace{0.03cm} \alpha_1\hspace{0.02cm}\alpha_2 \cdot \overline {x(t - t_1) \cdot x(t - t_2+ \tau)} + \hspace{0.05cm} \alpha_2\hspace{0.02cm}\alpha_1 \cdot \overline {x(t - t_2) \cdot x(t - t_1+ \tau)}\hspace{0.03cm} + \hspace{0.03cm} \alpha_2^2 \cdot \overline {x(t - t_2) \cdot x(t - t_2+ \tau)}. $$
- For the first and the last mean:
- $$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + \tau)} =\varphi_x(\tau).$$
- In contrast, for the second and third mean values, we obtain with $\Delta t = t_2 - t_1= 50 \ \rm ms$:
- $$\overline {x(t - t_1) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_2+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_1- t_2+ \tau)} =\varphi_x(\tau - \Delta t),$$
- $$\overline {x(t - t_2) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t - t_1+ \tau)} = \overline {x(t ) \hspace{0.05cm}\cdot \hspace{0.05cm}x(t + t_2- t_1+ \tau)} =\varphi_x(\tau + \Delta t).$$
- Total, this again results in a symmetric ACF, as shown in the graph below:
- $$\varphi_{y} (\tau) = {N_0}/{2} \cdot \left[ ( \alpha_1^2 \hspace{0.1cm} + \hspace{0.1cm} \alpha_2^2 ) \cdot {\rm \delta} (\tau) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau - \delta t) \hspace{0.1cm} + \hspace{0.1cm} \alpha_1 \cdot \alpha_2 \cdot {\rm \delta}(\tau + \Delta t) \right].$$
- $$\Rightarrow \hspace{0.3cm}\varphi_{y} (\tau = 0 ) \hspace{0.15cm}\underline{= 0.13 \cdot 10^{-6}\, {\rm W/Hz}}, \hspace{0.3cm}\varphi_{y} (\tau = \Delta t )\hspace{0.15cm}\underline{ = 0.025 \cdot 10^{-6}\, {\rm W/Hz}}.$$