Difference between revisions of "Aufgaben:Exercise 2.13: Inverse Burrows-Wheeler Transformation"
| (21 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Further_Source_Coding_Methods |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_A_2_14.png|right|frame|BWT result to be analyzed]] |
| − | + | The "Burrows–Wheeler Transformation" – abbreviated $\rm BWT$ – causes a blockwise sorting of the characters of a text with the aim of preparing the text for efficient data compression with the help of run-length coding or entropy coding. | |
| − | * | + | * First, an $N×N$ matrix is generated from a block of length $N$, with each row of this first matrix resulting from the preceding row by cyclic left shift. |
| − | * | + | * Then the matrix is sorted lexicographically (without special characters: alphabetically) . The result of the BWT is the last row of the new BWT matrix, the so-called $\text{L column}$ (from "Last"). |
| − | * | + | * Further, this task refers to the $\text{F column}$ (from "First", first row of the BWT matrix), which is needed for the inverse Burrows–Wheeler Transformation ⇒ reconstruction of the original text from the L column. |
| − | * | + | * For the inverse BWT, the so-called "primary index" $I$ is also required. This indicates the row of the BWT matrix in which the algorithm must be started. |
| − | + | The graphic shows the result of a BWT, more precisely its L column. The original text is to be reconstructed from this according to the description in the theory section [[Information_Theory/Further_Source_Coding_Methods#Burrows.E2.80.93Wheeler_transformation|Burrows–Wheeler Transformation]], | |
| + | *in subtask '''(2)''' with the primary index $I = 7$, | ||
| + | *in subtask '''(3)''' $I = 0$ is to be assumed. | ||
| − | |||
| − | |||
| − | |||
| Line 25: | Line 24: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <u>Hints:</u> | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Further_Source_Coding_Methods|Further Source Coding Methods]]. | ||
| + | *In particular, reference is made to the section [[Information_Theory/Further_Source_Coding_Methods#Burrows.E2.80.93Wheeler_transformation|Burrows–Wheeler Transformation]]. | ||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the $\text{F column}$ associated with the given $\text{L column}$ ? |
| − | |type=" | + | |type="()"} |
- $\rm SEINMEINDEIN$, | - $\rm SEINMEINDEIN$, | ||
- $\rm NIIINEEEDSMN$, | - $\rm NIIINEEEDSMN$, | ||
| Line 43: | Line 40: | ||
| − | { | + | {What is the result of the reconstruction with primary index $\underline{I = 7}$? |
| − | |type=" | + | |type="()"} |
+ $\rm MEINDEINSEIN$, | + $\rm MEINDEINSEIN$, | ||
- $\rm DEINSEINMEIN$, | - $\rm DEINSEINMEIN$, | ||
| Line 50: | Line 47: | ||
| − | { | + | {What happens if the reconstruction $\text{(inverse BWT transformation})$ starts from the wrong primary index $I = 0$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $\rm MEINDEINSEIN$, |
| − | + | + | + $\rm DEINSEINMEIN$, |
| + | - $\rm NIESNIEDNIEM$. | ||
| − | { | + | {Why is the Burrows–Wheeler transformation better suited than the original with regard to a later data compression? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It results in more favourable character frequencies. |
| − | - | + | - All characters are sorted lexicographically. |
| − | + | + | + Identical characters follow each other more often in the BWT. |
| Line 66: | Line 64: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The <u>solution suggestion 3</u> is correct: |
| − | * | + | *The first column of the BWT matrix is also called the "F column" and the last column the "L column" (from "First" or "Last"). |
| − | * | + | *Only the "L column" is passed on to the next coding level. |
| − | * | + | *The "F column", which is also needed for the reverse transformation, results from the "L column" by lexicographically sorting. |
| + | |||
| + | |||
| + | |||
| + | :[[File:Inf_Z_2_14b_v2.png|right|frame|Inverse BWT with $I = 7$ (left) or $I = 0$ (right)]] | ||
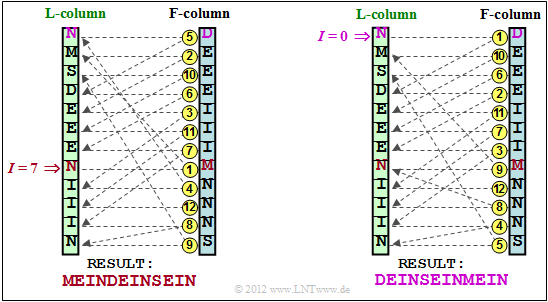
| + | '''(2)''' The <u>solution suggestion 1</u> is correct: <b>MEINDEINSEIN</b>, as can be seen from the left-hand representation of the following diagram. <br>Note that the top line represents the line number $I = 0$ in each case. For explanation: | ||
| + | * Start the decoding with the line $I = 7$ of the "F column". <br>The content is $\rm M$. | ||
| + | * Search for the corresponding $\rm M$ in the "L column" and find it in line number "1". | ||
| + | * From line 1 of the "L column" one goes horizontally to the "F column" and finds the symbol $\rm E$. | ||
| + | * Similarly, one finds the third output symbol $\rm I$ in line 4 of the "F column". | ||
| + | * The decoding algorithm ends with the output symbol $\rm N$ in the third last row. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(3)''' Correct is the <u>proposed solution 2</u>: $\rm DEINSEINMEIN$, as shown in the graph on the right. |
| + | <br clear=all> | ||
| − | '''(4)''' | + | '''(4)''' Correct is the <u>suggested solution 3</u>: |
| − | * | + | *In BWT, four characters here are equal to their predecessors, in the original none. |
| − | *In | + | *In the "F column", even more characters would be the same as their respective predecessors (6 in total) due to the lexicographical sorting, but this sorting cannot be reversed without loss. |
| − | * | + | *Solution suggestion 1 is wrong too: <br>The original and BWT contain exactly the same characters $($three times $\rm E$, three times $\rm I$, three times $\rm N$ and one each of $\rm D$, $\rm M$ and $\rm S)$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^2.4 Further Source Coding Methods^]] |
Latest revision as of 13:45, 17 November 2022
The "Burrows–Wheeler Transformation" – abbreviated $\rm BWT$ – causes a blockwise sorting of the characters of a text with the aim of preparing the text for efficient data compression with the help of run-length coding or entropy coding.
- First, an $N×N$ matrix is generated from a block of length $N$, with each row of this first matrix resulting from the preceding row by cyclic left shift.
- Then the matrix is sorted lexicographically (without special characters: alphabetically) . The result of the BWT is the last row of the new BWT matrix, the so-called $\text{L column}$ (from "Last").
- Further, this task refers to the $\text{F column}$ (from "First", first row of the BWT matrix), which is needed for the inverse Burrows–Wheeler Transformation ⇒ reconstruction of the original text from the L column.
- For the inverse BWT, the so-called "primary index" $I$ is also required. This indicates the row of the BWT matrix in which the algorithm must be started.
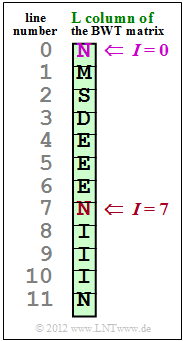
The graphic shows the result of a BWT, more precisely its L column. The original text is to be reconstructed from this according to the description in the theory section Burrows–Wheeler Transformation,
- in subtask (2) with the primary index $I = 7$,
- in subtask (3) $I = 0$ is to be assumed.
Hints:
- The exercise belongs to the chapter Further Source Coding Methods.
- In particular, reference is made to the section Burrows–Wheeler Transformation.
Questions
Solution
- The first column of the BWT matrix is also called the "F column" and the last column the "L column" (from "First" or "Last").
- Only the "L column" is passed on to the next coding level.
- The "F column", which is also needed for the reverse transformation, results from the "L column" by lexicographically sorting.
(2) The solution suggestion 1 is correct: MEINDEINSEIN, as can be seen from the left-hand representation of the following diagram.
Note that the top line represents the line number $I = 0$ in each case. For explanation:
- Start the decoding with the line $I = 7$ of the "F column".
The content is $\rm M$. - Search for the corresponding $\rm M$ in the "L column" and find it in line number "1".
- From line 1 of the "L column" one goes horizontally to the "F column" and finds the symbol $\rm E$.
- Similarly, one finds the third output symbol $\rm I$ in line 4 of the "F column".
- The decoding algorithm ends with the output symbol $\rm N$ in the third last row.
(3) Correct is the proposed solution 2: $\rm DEINSEINMEIN$, as shown in the graph on the right.
(4) Correct is the suggested solution 3:
- In BWT, four characters here are equal to their predecessors, in the original none.
- In the "F column", even more characters would be the same as their respective predecessors (6 in total) due to the lexicographical sorting, but this sorting cannot be reversed without loss.
- Solution suggestion 1 is wrong too:
The original and BWT contain exactly the same characters $($three times $\rm E$, three times $\rm I$, three times $\rm N$ and one each of $\rm D$, $\rm M$ and $\rm S)$.