Difference between revisions of "Aufgaben:Exercise 2.12Z: Reed-Solomon Syndrome Calculation"
| (14 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding}} |
| − | [[File: | + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representation as powers, polynomials, vectors]] |
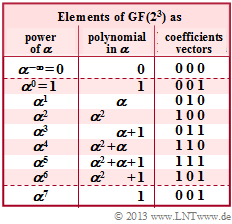
| − | + | As in the [[Aufgaben:Exercise_2.12:_Decoding_at_RSC_(7,_4,_4)_to_Base_8|"Exercise 2. 12"]] we consider the Reed–Solomon code $(7, \, 4, \, 4)_8$ based on the Galois field ${\rm GF}(q)$ with $q = 8 = 2^3$. The graph shows the corresponding conversion table. | |
| − | + | Given are the possible code symbols in | |
| + | # exponent representation $($powers of $\alpha)$ | ||
| + | # polynomialrepresentation, | ||
| + | # coefficient vector representation. | ||
| − | |||
| − | |||
| − | + | Given is the received word $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$. | |
| + | |||
| + | *Based on the syndrome $\underline {s} = (s_0, s_1, s_2) = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}$ it is to check whether individual symbols of the received vector $\underline{y}$ were falsified during transmission. | ||
| + | |||
| + | *Given is the parity-check matrix $\mathbf{H}$ of the considered code and its transpose: | ||
:$${ \boldsymbol{\rm H}} = | :$${ \boldsymbol{\rm H}} = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 29: | Line 34: | ||
| − | + | Hints: This exercise refers to the section [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Step_.28A.29:_Evaluation_of_the_syndrome_in_BDD| "Step (A): Evaluation of the syndrome in BDD"]] of the chapter "Error Correction according to Reed–Solomon Coding". | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 41: | Line 40: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {It holds for the weceived word: $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$. Specify the first element of the syndrome $\underline{s} = (s_0, \, s_1, \, s_2)$. |
|type="()"} | |type="()"} | ||
+ $s_0 = \alpha^4$, | + $s_0 = \alpha^4$, | ||
- $s_0 = \alpha^5$, | - $s_0 = \alpha^5$, | ||
- $s_0 = \alpha^6$, | - $s_0 = \alpha^6$, | ||
| − | - $s_0 = 0, \, 1, \, \alpha, \, \alpha^2$ | + | - $s_0 = 0, \, 1, \, \alpha, \, \alpha^2$ or $\alpha^3$. |
| − | { | + | {What is the second syndrome element for the same received word? |
|type="()"} | |type="()"} | ||
- $s_1 = \alpha^4$, | - $s_1 = \alpha^4$, | ||
+ $s_1 = \alpha^5$, | + $s_1 = \alpha^5$, | ||
- $s_1 = \alpha^6$, | - $s_1 = \alpha^6$, | ||
| − | - $s_1 = 0, \, 1, \, \alpha, \, \alpha^2$ | + | - $s_1 = 0, \, 1, \, \alpha, \, \alpha^2$ or $\alpha^3$. |
| − | { | + | {What is the third syndrome element for the same received word? |
|type="()"} | |type="()"} | ||
- $s_2 = \alpha^4$, | - $s_2 = \alpha^4$, | ||
| Line 64: | Line 63: | ||
- $s_2 = 0, \, 1, \, \alpha, \, \alpha^2$ oder $\alpha^3$. | - $s_2 = 0, \, 1, \, \alpha, \, \alpha^2$ oder $\alpha^3$. | ||
| − | { | + | {Known is that the received word $\underline{y}$ can be decoded correctly. How many symbol errors does the received word contain? |
|type="{}"} | |type="{}"} | ||
$r \ = \ ${ 1 3% } | $r \ = \ ${ 1 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File: | + | [[File:EN_KC_Z_2_5_neu.png|right|frame|Conversion tables for the Galois field $\rm GF(2^3)$]] |
| − | '''(1)''' | + | '''(1)''' The corresponding equation for syndrome calculation is: |
:$$\underline {s} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (s_0, s_1, s_2) = | :$$\underline {s} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (s_0, s_1, s_2) = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 88: | Line 87: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *The first element results in | |
:$$s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^2 + 1 \cdot \alpha^4 + \alpha \cdot \alpha^5= | :$$s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^2 + 1 \cdot \alpha^4 + \alpha \cdot \alpha^5= | ||
\alpha + \alpha^5 + \alpha^4+ \alpha^6$$ | \alpha + \alpha^5 + \alpha^4+ \alpha^6$$ | ||
:$$\Rightarrow\hspace{0.3cm} s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\alpha) + (\alpha^2 + \alpha+ 1)+ (\alpha^2 + \alpha) + + (\alpha^2 + 1) = \alpha^2 + \alpha = \alpha^4\hspace{0.05cm}.$$ | :$$\Rightarrow\hspace{0.3cm} s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\alpha) + (\alpha^2 + \alpha+ 1)+ (\alpha^2 + \alpha) + + (\alpha^2 + 1) = \alpha^2 + \alpha = \alpha^4\hspace{0.05cm}.$$ | ||
| − | + | *Correct is the <u>proposed solution 1</u>. | |
| − | '''(2)''' | + | '''(2)''' Correspondingly, for the second syndrome element, the <u>proposed solution 2</u> applies accordingly: |
:$$s_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^4 + 1 \cdot \alpha^1 + \alpha \cdot \alpha^3= | :$$s_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^4 + 1 \cdot \alpha^1 + \alpha \cdot \alpha^3= | ||
\alpha + \alpha^7 + \alpha+ \alpha^4= 1 + \alpha^4 = \alpha^2 + \alpha + 1 = \alpha^5 | \alpha + \alpha^7 + \alpha+ \alpha^4= 1 + \alpha^4 = \alpha^2 + \alpha + 1 = \alpha^5 | ||
| Line 102: | Line 101: | ||
| − | '''(3)''' | + | '''(3)''' To calculate $s_2$, the received word must be multiplied by the last matrix column: |
:$$s_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^6 + 1 \cdot \alpha^5 + \alpha \cdot \alpha^1= | :$$s_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^6 + 1 \cdot \alpha^5 + \alpha \cdot \alpha^1= | ||
\alpha + \alpha^2 + \alpha^5 + \alpha^2=\alpha^5 + \alpha = (\alpha^2 + \alpha + 1) + \alpha = \alpha^2 + 1 = \alpha^5 | \alpha + \alpha^2 + \alpha^5 + \alpha^2=\alpha^5 + \alpha = (\alpha^2 + \alpha + 1) + \alpha = \alpha^2 + 1 = \alpha^5 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Correct is the <u>proposed solution 3</u>. | |
| + | |||
| + | |||
| + | '''(4)''' Due to the calculated syndrome $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6) ≠ 0$, the received word contains at least one symbol error ⇒ $r > 0$. | ||
| + | *The present Reed–Solomon–code $(7, \, 4, \, 4)_8 \ \Rightarrow \ d_{\rm min} = 4$ cannot correct more than $t = ⌊d_{\rm min}/2⌋ = 1$ errors. | ||
| + | * Since the received word can actually be decoded according to the specification ⇒ $\underline{r = 1}$. | ||
| − | + | *Without this specification "The received word can be decoded", this subtask would not be solvable. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.5 Reed-Solomon Error Correction^]] |
Latest revision as of 16:30, 23 January 2023
As in the "Exercise 2. 12" we consider the Reed–Solomon code $(7, \, 4, \, 4)_8$ based on the Galois field ${\rm GF}(q)$ with $q = 8 = 2^3$. The graph shows the corresponding conversion table.
Given are the possible code symbols in
- exponent representation $($powers of $\alpha)$
- polynomialrepresentation,
- coefficient vector representation.
Given is the received word $\underline{y} = (\alpha, \, 0, \, \alpha^3, \, 0, \, 1, \, \alpha, \, 0)$.
- Based on the syndrome $\underline {s} = (s_0, s_1, s_2) = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}$ it is to check whether individual symbols of the received vector $\underline{y}$ were falsified during transmission.
- Given is the parity-check matrix $\mathbf{H}$ of the considered code and its transpose:
- $${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H}}^{\rm T} = \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$
Hints: This exercise refers to the section "Step (A): Evaluation of the syndrome in BDD" of the chapter "Error Correction according to Reed–Solomon Coding".
Questions
Solution
(1) The corresponding equation for syndrome calculation is:
- $$\underline {s} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (s_0, s_1, s_2) = \begin{pmatrix} \alpha,0, \alpha^3,0, 1, \alpha,0 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^2 \\ \alpha^4 & \alpha^1 & \alpha^{5} \\ \alpha^5 & \alpha^{3} & \alpha^{1} \\ \alpha^6 & \alpha^{5} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$
- The first element results in
- $$s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^2 + 1 \cdot \alpha^4 + \alpha \cdot \alpha^5= \alpha + \alpha^5 + \alpha^4+ \alpha^6$$
- $$\Rightarrow\hspace{0.3cm} s_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\alpha) + (\alpha^2 + \alpha+ 1)+ (\alpha^2 + \alpha) + + (\alpha^2 + 1) = \alpha^2 + \alpha = \alpha^4\hspace{0.05cm}.$$
- Correct is the proposed solution 1.
(2) Correspondingly, for the second syndrome element, the proposed solution 2 applies accordingly:
- $$s_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^4 + 1 \cdot \alpha^1 + \alpha \cdot \alpha^3= \alpha + \alpha^7 + \alpha+ \alpha^4= 1 + \alpha^4 = \alpha^2 + \alpha + 1 = \alpha^5 \hspace{0.05cm}.$$
(3) To calculate $s_2$, the received word must be multiplied by the last matrix column:
- $$s_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot 1 + \alpha^3 \cdot \alpha^6 + 1 \cdot \alpha^5 + \alpha \cdot \alpha^1= \alpha + \alpha^2 + \alpha^5 + \alpha^2=\alpha^5 + \alpha = (\alpha^2 + \alpha + 1) + \alpha = \alpha^2 + 1 = \alpha^5 \hspace{0.05cm}.$$
- Correct is the proposed solution 3.
(4) Due to the calculated syndrome $\underline{s} = (\alpha^4, \, \alpha^5, \, \alpha^6) ≠ 0$, the received word contains at least one symbol error ⇒ $r > 0$.
- The present Reed–Solomon–code $(7, \, 4, \, 4)_8 \ \Rightarrow \ d_{\rm min} = 4$ cannot correct more than $t = ⌊d_{\rm min}/2⌋ = 1$ errors.
- Since the received word can actually be decoded according to the specification ⇒ $\underline{r = 1}$.
- Without this specification "The received word can be decoded", this subtask would not be solvable.