Aufgaben:Exercise 4.7: Product Code Decoding

• Return to book

Syndrome tables of the considered component codes  $\mathcal{C}_1$  and  $\mathcal{C}_2$

We consider as in the  $\text{Exercise 4.6}$  a product code based on

• the Hamming code  $\rm HC \ (7, \ 4, \ 3)$   ⇒   $\mathcal{C}_1$,

• the truncated Hamming code  $\rm HC \ (6, \ 3, \ 3)$   ⇒   $\mathcal{C}_2$.

The parity-check matrices of these component codes are:

$${ \boldsymbol{\rm H}}_1 = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &1 &0 \\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm H}}_2 = \begin{pmatrix} 1 &1 &0 &1 &0 &0 \\ 1 &0 &1 &0 &1 &0 \\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

For the sake of completeness,  the generator matrices are also given,  but they are not needed to solve the exercise:

$${ \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1 \\ 0 &1 &0 &0 &1 &1 &0 \\ 0 &0 &1 &0 &0 &1 &1 \\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm G}}_2 = \begin{pmatrix} 1 &0 &0 &1 &1 &0 \\ 0 &1 &0 &1 &0 &1 \\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$

The  "Hard Decision Decoding"  of this code is preferably done iteratively,  by alternately  "syndrome decoding"  all rows and then all columns.  See section  "Iterative Syndrome Decoding of Product Codes".

Syndrome decoding of  (one-dimensional)  block codes has already been covered in the chapter  "Decoding of Linear Block Codes".  Here is a brief summary and an adaptation to the two-dimensional case:

1. From the received word  $\underline{y}$  $($a row or a column of the given received matrix$)$, 
   the syndrome corresponding to   $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$   resp.   $\underline{s} = \underline{y} \cdot \mathbf{H}_2^{\rm T}$   is formed.
2. With the result   $\underline{s} = \underline{s}_{\mu}$   one can read in above tables the so called  "coset leader"  $\underline{e}_{\mu}$ .
3. The corrected code word is then  $\underline{y} + \underline{e}_{\mu}$.

Predefined encoder and receiver matrices

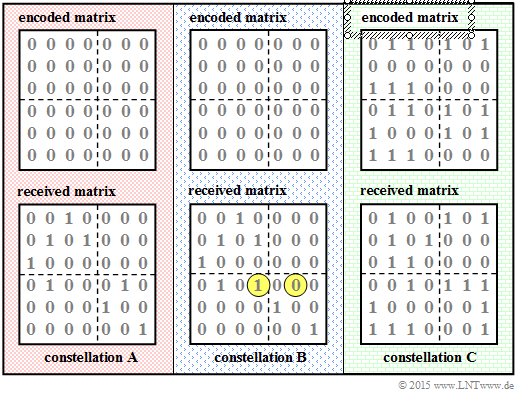
The accompanying diagram shows three different encoded and received matrices to be analyzed in the subtasks  (1),  (2),  and  (3):

• We name them constellation  $\mathbf{A}$,  $\mathbf{B}$  and  $\mathbf{C}$.

• Marked in yellow are the differences in the received matrices of constellation  $\mathbf{B}$  versus  $\mathbf{A}$.  In both cases,  the encoded matrix consists only of  "zeros".

• The encoded matrix of  $\rm C$  was determined in  $\text{Exercise 4.6}$ .

Hints:

• This exercise belongs to the chapter  "Basics of Product Codes".

• Reference is made in particular to the section  "Iterative syndrome decoding of product codes".

Questions

1

Is the two-dimensional received matrix  $\mathbf{A}$  decodable?

	Yes,  after the first decoding in horizontal direction.
	Yes,  after the first decoding in vertical direction.
	Yes,  after the second decoding in horizontal direction.
	Yes,  after the second decoding in vertical direction.
	No.

2

Is the two-dimensional received matrix  $\mathbf{B}$  decodable?

	Yes,  after the first decoding in horizontal direction.
	Yes,  after the first decoding in vertical direction.
	Yes,  after the second decoding in horizontal direction.
	Yes,  after the second decoding in vertical direction.
	No.

3

Is the two-dimensional received matrix  $\mathbf{C}$  decodable? 
Try to find the solution via an equivalence to subtask  (1)  resp.  (2).

	Yes,  after the first decoding in horizontal direction.
	Yes,  after the first decoding in vertical direction.
	Yes,  after the second decoding in horizontal direction.
	Yes,  after the second decoding in vertical direction.
	No.

Solution

Solution

(1)  The decoding process of the received matrix  $\mathbf{A}$  is illustrated by the following diagram.

Syndrome decoding of the two-dimensional received matrix $\mathbf{A}$

• The single errors in rows  1, 3, 5 and 6  are detected by  $(7, \ 4, \ 3)$  Hamming code and can be corrected
   ⇒  green markings in the graphic  "1st iteration horizontal".

• For the second row results the syndrome

$$\underline{s} = \underline{y}_2 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 \\ 1 &1 &0 \\ 0 &1 &1 \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} \hspace{-0.05cm}=$$

$$\Rightarrow \hspace{0.3cm} \underline{s} = \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1 \hspace{0.03cm}.$$

• According to the upper syndrome table on the information page,  the last bit is incorrectly  "corrected".  Incorrect corrections are entered in red in the upper graphic.

• Correspondingly applies to the fourth row:

$$\underline{s} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0 \right ) \cdot { \boldsymbol{\rm H}}_1^{\rm T} = \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right )= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \underline{s}_4 \hspace{0.05cm}.$$

• This causes a miscorrection of bit  5.

• Vertical decoding of columns 1, 3, 4, 5, 6, and 7 is straightforward because there is at most one error per column, which can be corrected by the truncated Hamming code $\rm (6, \ 3, \ 3)$.

• In column 2, however, there is a miscorrection of the last bit according to the lower syndrome table. With the transpose of the $\rm (6, \ 3, \ 3)$ parity-check matrix $\mathbf{H}_2$ results namely:

$$\underline{s}= \underline{y}_{2{\rm S}}\cdot { \boldsymbol{\rm H}}_2^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \begin{pmatrix} 1 &1 &0 \\ 1 &0 &1 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) + \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1.$$

• The second horizontal decoding is problem-free, since now at most one error occurs in each row  ⇒  Solution suggestion 3.

(2)  The following graphic shows the decoding process according to the specifications given by  $\mathbf{B}$. 

For syndrome decoding of the two-dimensional received matrix  $\mathbf{B}$.

Despite only minor modifications compared to  $\mathbf{A}$,  there are now serious differences:

• Due to the first horizontal decoding,  the  "corrected"  rows 2 and 4 now read equally:  $(0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1)$, i.e.,  the last bit of these rows is miscorrected in each case.

• Vertical decoding results in identical columns 2, 4, and 6:  $(0, \, 1, \, 0, \, 1, \, 0, \, 1)$.  After that,  there are three  "ones"  $($or none$)$  in each row and in each column.

• This constellation remains for arbitrary further (horizontal or vertical) decodings, because for $d_{\rm min} = 3$ always the syndrome $\underline{s}_0 = (0, \, 0, \, 0)$ results.

The correct solution is  proposal 5.

Matrix representation of encoder, receiver and error pattern

(3)  Comparing the encoded and received matrices  $($differences are marked in blue$)$,  one can create the error matrices by modulo-2 additions according to the following graph.

The error matrix is equal to the received matrix of $\mathbf{A}$  ⇒  again, proposed solution 3 is correct.