Difference between revisions of "Applets:Diskrete Fouriertransformation und Inverse"
m (Guenter verschob die Seite Diskrete Fouriertransformation und Inverse (Applet) nach Diskrete Fouriertransformation und Inverse) |
m (Text replacement - "„" to """) |
||
| (26 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|dft}} |
| − | + | ||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
<br> | <br> | ||
| Line 16: | Line 16: | ||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
<br> | <br> | ||
| − | === | + | ===Argumente für die diskrete Realisierung der Fouriertransformation=== |
| + | |||
| + | Die '''Fouriertransformation''' gemäß der herkömmlichen Beschreibung für zeitkontinuierliche Signale weist aufgrund der unbegrenzten Ausdehnung des Integrationsintervalls eine unendlich hohe Selektivität auf und ist deshalb ein ideales theoretisches Hilfsmittel der Spektralanalyse. | ||
| + | |||
| + | Sollen die Spektralanteile $X(f)$ einer Zeitfunktion $x(t)$ numerisch ermittelt werden, so sind die allgemeinen Transformationsgleichungen | ||
| + | |||
| + | :$$\begin{align*}X(f) & = \int_{-\infty | ||
| + | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Hintransformation}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{Erstes Fourierintegral} | ||
| + | \hspace{0.05cm},\\ | ||
| + | x(t) & = \int_{-\infty | ||
| + | }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} | ||
| + | \text{Rücktransformation}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{Zweites Fourierintegral} | ||
| + | \hspace{0.05cm}\end{align*}$$ | ||
| + | |||
| + | aus zwei Gründen ungeeignet: | ||
| + | *Die Gleichungen gelten ausschließlich für zeitkontinuierliche Signale. Mit Digitalrechnern oder Signalprozessoren kann man jedoch nur zeitdiskrete Signale verarbeiten. | ||
| + | *Für eine numerische Auswertung der beiden Fourierintegrale ist es erforderlich, das jeweilige Integrationsintervall auf einen endlichen Wert zu begrenzen. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Daraus ergibt sich folgende Konsequenz:}$ | ||
| − | + | Ein '''kontinuierliches Signal''' muss vor der numerischen Bestimmung seiner Spektraleigenschaften zwei Prozesse durchlaufen, nämlich | |
| + | *den der '''Abtastung''' zur Diskretisierung, und | ||
| + | *den der '''Fensterung''' zur Begrenzung des Integrationsintervalls.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Im Folgenden wird ausgehend von einer aperiodischen Zeitfunktion $x(t)$ und dem dazugehörigen Fourierspektrum $X(f)$ eine für die Rechnerverarbeitung geeignete zeit– und frequenzdiskrete Beschreibung vorgestellt. | |
| − | |||
| − | |||
| − | |||
| − | + | ===Zeitdiskretisierung – Periodifizierung im Frequenzbereich=== | |
| − | |||
| − | |||
| − | + | Die folgenden Grafiken zeigen einheitlich links den Zeitbereich und rechts den Frequenzbereich. Ohne Einschränkung der Allgemeingültigkeit sind $x(t)$ und $X(f)$ jeweils reell und gaußförmig. | |
| − | |||
| − | |||
| + | [[File:P_ID1132__Sig_T_5_1_S2_neu.png|center|frame|Diskretisierung im Zeitbereich – Periodifizierung im Frequenzbereich]] | ||
| − | + | Man kann die Abtastung des Zeitsignals $x(t)$ durch die Multiplikation mit einem Diracpuls $p_{\delta}(t)$ beschreiben. Es ergibt sich das im Abstand $T_{\rm A}$ abgetastete Zeitsignal | |
| − | + | ||
| − | :$$ | + | :$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot |
| − | + | \delta (t- \nu \cdot T_{\rm A} | |
| − | + | )\hspace{0.05cm}.$$ | |
| − | {{ | + | Dieses abgetastete Signal $\text{A}\{ x(t)\}$ transformieren wir nun in den Frequenzbereich. Der Multiplikation des Diracpulses $p_{\delta}(t)$ mit $x(t)$ entspricht im Frequenzbereich die Faltung von $P_{\delta}(f)$ mit $X(f)$. Es ergibt sich das periodifizierte Spektrum $\text{P}\{ X(f)\}$, wobei $f_{\rm P}$ die Frequenzperiode der Funktion $\text{P}\{ X(f)\}$ angibt: |
| − | $\text{ | + | |
| − | + | :$${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} | |
| − | * | + | X (f- \mu \cdot f_{\rm P} )\hspace{0.5cm} {\rm mit }\hspace{0.5cm}f_{\rm |
| − | * | + | P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$ |
| − | + | ||
| − | + | *Das abgetastete Signal nennen wir $\text{A}\{ x(t)\}$. | |
| − | + | * Die '''Frequenzperiode''' wird mit $f_{\rm P}$ = $1/T_{\rm A}$ bezeichnet. | |
| + | |||
| + | |||
| + | Die obige Grafik zeigt den hier beschriebenen Funktionalzusammenhang. Es ist anzumerken: | ||
| + | *Die Frequenzperiode $f_{\rm P}$ wurde hier bewusst klein gewählt, so dass die Überlappung der zu summierenden Spektren deutlich zu erkennen ist. | ||
| + | *In der Praxis sollte $f_{\rm P}$ aufgrund des Abtasttheorems mindestens doppelt so groß sein wie die größte im Signal $x(t)$ enthaltene Frequenz. | ||
| + | *Ist dies nicht erfüllt, so muss mit '''Aliasing''' gerechnet werden. | ||
| + | |||
| + | |||
| + | |||
| + | ===Frequenzdiskretisierung – Periodifizierung im Zeitbereich=== | ||
| + | |||
| + | Die Diskretisierung von $X(f)$ lässt sich ebenfalls durch eine Multiplikation mit einem Diracpuls beschreiben. Es ergibt sich das im Abstand $f_{\rm A}$ abgetastete Spektrum: | ||
| + | |||
| + | :$${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} | ||
| + | f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} | ||
| + | f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$ | ||
| + | |||
| + | Transformiert man den hier verwendeten Frequenz–Diracpuls $($mit Impulsgewichten $f_{\rm A})$ in den Zeitbereich, so erhält man mit $T_{\rm P} = 1/f_{\rm A}$: | ||
| + | |||
| + | :$$\sum_{\mu = - \infty }^{+\infty} | ||
| + | f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} | ||
| + | \sum_{\nu = - \infty }^{+\infty} | ||
| + | \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Multiplikation mit $X(f)$ entspricht im Zeitbereich der Faltung mit $x(t)$. Man erhält das im Abstand $T_{\rm P}$ periodifizierte Signal $\text{P}\{ x(t)\}$: | ||
| + | |||
| + | :$${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} | ||
| + | {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} | ||
| + | \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} | ||
| + | x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$ | ||
| + | |||
| + | [[File:P_ID1134__Sig_T_5_1_S3_neu.png|right|frame|Diskretisierung im Frequenzbereich – Periodifizierung im Zeitbereich]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ | ||
| + | Dieser Zusammenhang ist in der Grafik veranschaulicht: | ||
| + | *Aufgrund der groben Frequenzrasterung ergibt sich in diesem Beispiel für die Zeitperiode $T_{\rm P}$ ein relativ kleiner Wert. | ||
| − | |||
| − | + | * Deshalb unterscheidet sich das (blaue) periodifizierte Zeitsignal $\text{P}\{ x(t)\}$ aufgrund von Überlappungen deutlich von $x(t)$.}} | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Finite Signaldarstellung=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | ||
| − | [[File: | + | [[File:P_ID1135__Sig_T_5_1_S4_neu.png|right|frame|Finite Signale der Diskreten Fouriertransformation (DFT)]] |
| − | + | Zur so genannten ''finiten Signaldarstellung'' kommt man, | |
| + | *wenn sowohl die Zeitfunktion $x(t)$ | ||
| + | *als auch die Spektralfunktion $X(f)$ | ||
| − | |||
| − | + | ausschließlich durch ihre Abtastwerte angegeben werden. | |
| − | |||
| − | |||
| − | |||
<br clear=all> | <br clear=all> | ||
| − | === | + | Die Grafik ist wie folgt zu interpretieren: |
| + | *Im linken Bild blau eingezeichnet ist die Funktion $\text{A}\{ \text{P}\{ x(t)\}\}$. Diese ergibt sich durch Abtastung der periodifizierten Zeitfunktion $\text{P}\{ x(t)\}$ mit äquidistanten Diracimpulsen im Abstand $T_{\rm A} = 1/f_{\rm P}$. | ||
| + | *Im rechten Bild grün eingezeichnet ist die Funktion $\text{P}\{ \text{A}\{ X(f)\}\}$. Diese ergibt sich durch Periodifizierung $($mit $f_{\rm P})$ der abgetasteten Spektralfunktion $\{ \text{A}\{ X(f)\}\}$. | ||
| + | *Zwischen dem blauen finiten Signal und dem grünen finiten Signal besteht ebenfalls eine Fourierkorrespondenz, und zwar die folgende: | ||
| + | |||
| + | :$${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | Die Diraclinien der periodischen Fortsetzung $\text{P}\{ \text{A}\{ X(f)\}\}$ der abgetasteten Spektralfunktion fallen allerdings nur dann in das gleiche Frequenzraster wie diejenigen von $\text{A}\{ X(f)\}$, wenn die Frequenzperiode $f_{\rm P}$ ein ganzzahliges Vielfaches $(N)$ des Frequenzabtastabstandes $f_{\rm A}$ ist. | ||
| + | |||
| + | *Bei Anwendung der finiten Signaldarstellung muss stets die folgende Bedingung erfüllt sein, wobei für die natürliche Zahl $N$ in der Praxis meist eine Zweierpotenz verwendet wird (der obigen Grafik liegt der Wert $N = 8$ zugrunde): | ||
| + | |||
| + | :$$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A} }= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} | ||
| + | N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$}} | ||
| + | |||
| + | |||
| + | Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt: | ||
| + | |||
| + | :$${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | ||
| + | {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Fazit:}$ | ||
| + | *Die Zeitfunktion $\text{P}\{ \text{A}\{ x(t)\}\}$ besitzt die Periode $T_{\rm P} = N \cdot T_{\rm A}$. | ||
| + | *Die Periode im Frequenzbereich ist $f_{\rm P} = N \cdot f_{\rm A}$. | ||
| + | *Zur Beschreibung des diskretisierten Zeit– und Frequenzverlaufs reichen somit jeweils $N$ '''komplexe Zahlenwerte''' in Form von Impulsgewichten aus.}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
| + | Es liegt ein zeitbegrenztes (impulsartiges) Signal $x(t)$ in abgetasteter Form vor, wobei der Abstand zweier Abtastwerte $T_{\rm A} = 1\, {\rm µ s}$ beträgt: | ||
| + | *Nach einer diskreten Fouriertransformation mit $N = 512$ liegt das Spektrum $X(f)$ in Form von Abtastwerten im Abstand $f_{\rm A} = (N \cdot T_{\rm A})^{–1} \approx 1.953\,\text{kHz} $ vor. | ||
| + | *Vergrößert man den DFT–Parameter auf $N= 2048$, so ergibt sich ein feineres Frequenzraster mit $f_{\rm A} \approx 488\,\text{Hz}$.}} | ||
| + | |||
| + | |||
| + | |||
| + | ===Diskrete Fouriertransformation=== | ||
| + | |||
| + | Aus dem herkömmlichen "ersten Fourierintegral" | ||
| + | |||
| + | :$$X(f) =\int_{-\infty | ||
| + | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$ | ||
| + | |||
| + | entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion | ||
| + | |||
| + | :$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} | ||
| + | {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} | ||
| + | \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$ | ||
| + | |||
| + | Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind. | ||
| + | |||
| + | Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor: | ||
| + | *Die $N$ '''Zeitbereichskoeffizienten''' seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$: | ||
| + | :$$d(\nu) = | ||
| + | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$ | ||
| + | *Die $N$ '''Frequenzbereichskoeffizienten''' seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1: | ||
| + | :$$D(\mu) = f_{\rm A} \cdot | ||
| + | {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$ | ||
| + | *Abkürzend wird für den von $N$ abhängigen '''komplexen Drehfaktor''' geschrieben: | ||
| + | :$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} | ||
| + | = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | [[File:P_ID2730__Sig_T_5_1_S5_neu.png|right|frame|Zur Definition der Diskreten Fouriertransformation (DFT) mit $N=8$]] | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | |||
| + | Unter dem Begriff '''Diskrete Fouriertransformation''' (kurz '''DFT''') versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$: | ||
| + | |||
| + | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} | ||
| + | d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$ | ||
| + | |||
| + | In der Grafik erkennt man an einem Beispiel | ||
| + | *die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung, | ||
| + | *die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.}} | ||
| + | |||
| + | |||
| + | ===Inverse Diskrete Fouriertransformation=== | ||
| + | |||
| + | Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das "zweite Fourierintegral" | ||
| + | |||
| + | :$$\begin{align*}x(t) & = \int_{-\infty | ||
| + | }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} | ||
| + | t}\hspace{0.1cm} {\rm d}f\end{align*}$$ | ||
| − | + | in diskretisierter Form: $d(\nu) = | |
| − | + | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | |
| + | A}}\hspace{0.01cm}.$ | ||
| − | + | [[File:P_ID2731__Sig_T_5_1_S6_neu.png|right|frame|Zur Definition der IDFT mit $N=8$]] | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Definition:}$ | |
| − | |||
| − | + | Unter dem Begriff '''Inverse Diskrete Fouriertransformation''' (kurz '''IDFT''') versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$: | |
| − | :$$\ | + | |
| + | :$$d(\nu) = \sum_{\mu = 0 }^{N-1} | ||
| + | D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| + | Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier: | ||
| + | :$$d(\nu) = | ||
| + | {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm | ||
| + | A} }\hspace{0.01cm},$$ | ||
| + | |||
| + | :$$D(\mu) = f_{\rm A} \cdot | ||
| + | {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } | ||
| + | \hspace{0.01cm},$$ | ||
| + | :$$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} | ||
| + | \hspace{0.01cm}.$$}} | ||
| − | + | ||
| + | Ein Vergleich zwischen DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind: | ||
| + | *Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen. | ||
| + | *Bei der IDFT entfällt die Division durch $N$. | ||
| − | |||
| − | < | + | ===Interpretation von DFT und IDFT=== |
| − | + | <br> | |
| − | + | Die Grafik zeigt die diskreten Koeffizienten im Zeit– und Frequenzbereich zusammen mit den periodifizierten zeitkontinuierlichen Funktionen. | |
| − | : | + | [[File:P_ID1136__Sig_T_5_1_S7_neu.png|center|frame|Zeit– und Frequenzbereichskoeffizienten der DFT]] |
| − | |||
| − | *Die | + | Bei Anwendung von DFT bzw. IDFT ist zu beachten: |
| − | * | + | *Nach obigen Definitionen besitzen die DFT–Koeffizienten $d(ν)$ und $D(\mu)$ stets die Einheit der Zeitfunktion. |
| + | *Dividiert man $D(\mu)$ durch $f_{\rm A}$, so erhält man den Spektralwert $X(\mu \cdot f_{\rm A})$. | ||
| + | *Die Spektralkoeffizienten $D(\mu)$ müssen stets komplex angesetzt werden, um auch ungerade Zeitfunktionen berücksichtigen zu können. | ||
| + | *Um auch Bandpass–Signale im äquivalenten Tiefpass–Bereich transformieren zu können, verwendet man meist auch komplexe Zeitkoeffizienten $d(\nu)$. | ||
| + | *Als Grundintervall für $\nu$ und $\mu$ definiert man meist – wie in obiger Grafik – den Bereich von $0$ bis $N - 1$. | ||
| + | *Mit den komplexwertigen Zahlenfolgen $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.1cm}\rangle$ sowie $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.1cm}\rangle$ werden DFT und IDFT ähnlich wie die herkömmliche Fouriertransformation symbolisiert: | ||
| + | :$$\langle \hspace{0.1cm} D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$ | ||
| + | *Ist die Zeitfunktion $x(t)$ bereits auf den Bereich $0 \le t \lt N \cdot T_{\rm A}$ begrenzt, dann geben die von der IDFT ausgegebenen Zeitkoeffizienten direkt die Abtastwerte der Zeitfunktion an: $d(\nu) = x(\nu \cdot T_{\rm A}).$ | ||
| + | *Ist $x(t)$ gegenüber dem Grundintervall verschoben, so muss man die im $\text{Beispiel 3}$ gezeigte Zuordnung zwischen $x(t)$ und den Koeffizienten $d(\nu)$ wählen. | ||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 3:}$ | |
| − | + | Die obere Grafik zeigt den unsymmetrischen Dreieckimpuls $x(t)$, dessen absolute Breite kleiner ist als $T_{\rm P} = N \cdot T_{\rm A}$. | |
| − | :$$\ | + | |
| − | * | + | [[File:P_ID1139__Sig_T_5_1_S7b_neu.png|right|frame|Zur Belegung der DFT-Koeffizienten mit $N=8$]] |
| − | + | ||
| − | + | Die untere Skizze zeigt die zugeordneten DFT–Koeffizienten gültig für $N = 8$ | |
| − | + | ||
| + | *Für $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$ gilt $d(\nu) = x(\nu \cdot T_{\rm A})$: | ||
| + | |||
| + | :$$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} | ||
| + | d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} | ||
| + | d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$ | ||
| + | :$$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} | ||
| + | d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$ | ||
| + | *Dagegen sind die Koeffizienten $d(5)$, $d(6)$ und d$(7)$ wie folgt zu setzen: | ||
| + | |||
| + | :$$d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ) $$ | ||
| − | + | :$$ \Rightarrow \hspace{0.2cm}d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} | |
| − | $\ | + | d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} |
| − | + | d(7) = x (-T_{\rm A})\hspace{0.05cm}.$$ }} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br><br> | <br><br> | ||
| Line 153: | Line 284: | ||
*Wählen Sie zunächst die Nummer ('''1''', ...) der zu bearbeitenden Aufgabe. | *Wählen Sie zunächst die Nummer ('''1''', ...) der zu bearbeitenden Aufgabe. | ||
*Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. | *Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. | ||
| − | *Lösung nach Drücken von | + | *Lösung nach Drücken von "Musterlösung". |
| − | |||
| − | |||
| − | Die Nummer '''0''' entspricht einem | + | |
| + | Die Nummer '''0''' entspricht einem "Reset": | ||
*Gleiche Einstellung wie beim Programmstart. | *Gleiche Einstellung wie beim Programmstart. | ||
| − | *Ausgabe eines | + | *Ausgabe eines "Reset–Textes" mit weiteren Erläuterungen zum Applet. |
| + | {{BlaueBox|TEXT= | ||
| + | '''(1)''' Neue Einstellung: $\text{DFT von Signal (b): Gleichsignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen $\text{FT}$ ?}} | ||
| + | |||
| + | ::* Im Zeitbereich sind alle $d(\nu) =1$. Im Frequenzbereich sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(0)] =1$. | ||
| + | ::* Dies entspricht bei der herkömmlichen (zeitkontinuierlichen) Fouriertransformation: $x(t) = A\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = A \cdot \delta(f=0)$ mit $A=1$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(2)''' Gehen Sie vom erhaltenen $D(\mu)$–Feld aus und verschieben Sie alle Koeffizienten um eine Stelle nach unten. Welche Zeitfunktion liefert die $\rm IDFT$? }} |
| − | ::* $\ | + | ::* Nun sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Das Zeitbereichsergebnis ist eine komplexe Exponentialfunktion. |
| − | ::* | + | ::* Der Realteil des $d(\nu)$–Feldes zeigt einen Cosinus und der Imaginärteil eine Sinusfunktion. Bei beiden Funktionen erkennt man jeweils eine Periode. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(3)''' Ergänzen Sie das aktuelle $D(\mu)$–Feld um den Koeffizienten ${\rm Im}\big [D(1)] =1$. Welche Unterschiede erkennt man gegenüber '''(2)''' im Zeitbereich? }} |
| − | ::* | + | ::* Zum einen erkennt man nun bei Realteil und Imaginärteil eine Phasenverschiebung um zwei Stützwerte. Dies entspricht der Phase $\varphi = 45^\circ$. |
| − | ::* | + | ::* Zudem wurden die Amplituden von Real– und Imaginärteil jeweils um den Faktor $\sqrt{2}$ vergrößert. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(4)''' Setzen Sie das $D(\mu)$–Feld auf Null mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Durch welchen zusätzlichen $D(\mu)$–Koeffizienten erhält man ein reelles $d(\nu)$–Feld?}} |
| − | ::* | + | ::* Durch Probieren oder Nachdenken erkennt man, dass auch ${\rm Re}\big [D(15)] =1$ gesetzt werden muss. Dann beschreibt das $d(\nu)$–Feld einen Cosinus. |
| − | ::* Das | + | ::* Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = 2 \cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = \delta(f -f_0)+\delta(f +f_0)$. |
| + | ::* Das Feld $D(1)$ steht für die Frequenz $+f_0$ und aufgrund der Periodizät mit $N=16$ wird die Frequenz $-f_0$ durch $D(15) = D(-1)$ ausgedrückt. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(5)''' Mit welchem $D(\mu)$–Feld erhält man nach der $\rm IDFT$ im $d(\nu)$–Feld eine reelle Cosinusfunktion mit der Amplitude $A=1$?}} |
| − | ::* | + | ::* Die Diskrete Fouriertransformation ist ebenso wie die herkömmliche Fouriertransformation linear ⇒ $D(1) = D(15)=0.5$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(6)''' Neue Einstellung: $\text{DFT von Signal (e): Cosinussignal}$ und anschließende Signalverschiebungen. Was bewirken diese Verschiebungen im Frequenzbereich? }} |
| − | ::* | + | ::* Eine Verschiebung im Zeitbereich verändert das Cosinussignal zu einer "Harmonischen Schwingung" mit beliebiger Phase. |
| − | ::* | + | ::* Das $D(\mu)$–Feld ist weiterhin Null bis auf $D(1)$ und $D(15)$. Die Beträge $|D(1)|$ und $|D(15)|$ bleiben ebenfalls gleich. |
| − | ::* | + | ::* Die alleinige Veränderung betrifft die Phase, also die unterschiedliche Aufteilung der Beträge auf Real– und Imaginärteil. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(7)''' Neue Einstellung: $\text{DFT von Signal (f): Sinussignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen $\text{FT}$ ?}} |
| − | ::* Für $\ | + | ::* Das Sinussignal ergibt sich aus dem Cosinussignal durch vier Zeitverschiebungen. Deshalb gelten alle Aussagen von '''(6)''' weiterhin. |
| + | ::* Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = {\rm j}/2 \cdot \big [\delta(f +f_0)-\delta(f -f_0)\big ]$. | ||
| + | ::* Der Koeffizient $D(1)$ ⇒ $($Frequenz: $+f_0)$ ist imaginär und hat den Imaginärteil $-0.5$. Entsprechend gilt ${\rm Im}\big [D(15)] =+0.5$ ⇒ $($Frequenz: $-f_0)$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(8)''' Neue Einstellung: $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$. Interpretieren Sie das Ergebnis im Vergleich zur Aufgabe '''(5)'''.}} |
| − | ::* | + | ::* Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (2f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -2 f_0)+0.5 \cdot \delta(f +2f_0)$. |
| + | ::* Für die Frequenz $2f_0$ steht das Feld $D(2)$ und für die Frequenz $-2f_0$ aufgrund der Periodizät das Feld $D(14) = D(-2)$ : $D(2) = D(14) = 0.5$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(9)''' Untersuchen Sie nun den Fall $\text{DFT von Sinussignal (zwei Perioden)}$. Welche Einstellung müssen Sie vornehmen? Interpretieren Sie das Ergebnis.}} |
| − | ::* | + | ::* Zum gewünschten Signal kommt man von $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$ mit zwei Verschiebungen. Bei '''(7)''': Vier Verschiebungen. |
| − | + | ::* Das DFT–Ergebnis lautet dementsprechend: ${\rm Im}\big [D(2)] =-0.5$ und ${\rm Im}\big [D(14)] =+0.5$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(10)''' Neue Einstellung: $\text{DFT von (h) Alternierende Zeitkoeffizienten}$. Interpretieren Sie das DFT–Ergebnis.}} |
| − | ::* | + | ::* Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (8f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -8 f_0)+0.5 \cdot \delta(f +8f_0)$. |
| + | ::* $8f_0$ ist die höchste mit $N=16$ in der DFT darstellbare Frequenz. Pro Periodendauer gibt es nur zwei Abtastwerte, nämlich $+1$ und $-1$. | ||
| + | ::* Unterschied zur Teilaufgabe '''(5)''': Aus $D(1) =0.5$ wird nun $D(8) =0.5$. Ebenso verschiebt sich $D(15) =0.5$ auf $D(8) =0.5$. Endergebnis: $D(8) =1$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(11)''' Welche Unterschiede erhält man mit den beiden Einstellungen $\text{DFT von Signal (i): Diracimpuls}$ sowie $\text{IDFT von Spektrum (I): Diracspektrum}$ ?}} |
| − | ::* | + | ::* Keine! Im ersten Fall sind alle Koeffizienten $D(\mu) = 1$ (reell); im zweiten Fall dagegen in äquivalenter Weise die Koeffizienten $d(\nu) = 1$ (reell). |
| − | ::* | + | |
| − | ::* | + | {{BlaueBox|TEXT= |
| + | '''(12)''' Gibt es Unterschiede, wenn man im jeweiligen Eingabefeld die reelle $1$ um jeweils eine Stelle nach unten verschiebt, also $d(\nu=1) = 1$ bzw. $D(\mu=1) = 1$?}} | ||
| + | ::* Im ersten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen. | ||
| + | ::* Im zweiten Fall ⇒ ${\rm Re}\big [D(\mu=1)] = 1$ ergibt sich im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit positivem Vorzeichen. | ||
| + | ::* ''Hinweis'': Mit ${\rm Re}\big [D(\mu=15)] = 1$ ergäbe sich auch im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit negativem Vorzeichen. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(13)''' Neue Einstellung: $\text{DFT von Signal (k): Dreieckimpuls}$. Interpretieren Sie die $d(\nu)$–Belegungunter der Annahme $T_{\rm A} = 1 \ \rm ms$.}} | ||
| + | |||
| + | ::* Wählen Sie die Betragsdarstellung. $x(t)$ ist symmetrisch um $t=0$ und erstreckt sich von $-8 \cdot T_{\rm A} = -8 \ \rm ms$ bis $+8 \cdot T_{\rm A} = +8 \ \rm ms$. | ||
| + | ::* $d(\nu)$–Belegung: $d(0)=x(0)= 1$, $d(1)=x(T_{\rm A})= 0.875$, ... , $d(8)=x(8T_{\rm A})= 0$, $d(9)=x(-7T_{\rm A})= 0.125$, ..., $d(15)=x(-T_{\rm A})= 0.875$. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(14)''' Gleiche Einstellung wie bei '''(13)'''. Interpretieren Sie das DFT–Ergebnis, insbesondere die Koeffizienten $D(0)$, $D(1)$, $D(2)$ und $D(15)$.}} | ||
| + | |||
| + | ::* Im Frequenzbereich steht $D(0)$ für die Frequenz $f= 0$ und $D(1)$ und $D(15)$ für die Frequenzen $\pm f_{\rm A}$. Es gilt $f_{\rm A} = 1/(N \cdot T_{\rm A}) = 62.5\text{ Hz}$. | ||
| + | ::* Für den Wert des kontinuierlichen Spektrums bei $f=0$ gilt $X(f=0)=D(0)/f_{\rm A} = 0.5/(0.0625\text{ kHz}) = 8\cdot \text{ kHz}^{-1}$. | ||
| + | ::*Die erste Nullstelle des ${\rm si}^2$–förmigen Spektrums $X(f)$ tritt bei $2 \cdot f_{\rm A}= 125\text{ Hz}$ auf. Die weiteren Nullstellen sind äquidistant. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(15)''' Neue Einstellung: $\text{DFT von Signal (i): Rechteckimpuls}$. Interpretieren Sie die dargestellten Ergebnisse.}} | ||
| + | |||
| + | ::* Das eingestellte (symmetrische) Rechteck erstreckt sich über $\pm 4 \cdot T_{\rm A}$. An den Rändern sind die Zeitkoeffizienten nur halb so groß: $d(4) = d(12) =0.5$. | ||
| + | ::* Die weiteren Aussagen von '''(14)''' gelten auch für dieses ${\rm si}$–förmige Spektrum $X(f)$. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(16)''' Gleiche Einstellung wie bei '''(15)'''. Welche Modifikationen sind am $d(\nu)$–Feld vorzunehmen, um die Rechteckdauer zu halbieren ⇒ $\pm 2 \cdot T_{\rm A}$.}} | ||
| + | |||
| + | ::* $d(0) = d(1) = d(15) =1, \ d(2) = d(14) = 0.5$. Alle anderen Zeitkoeffizienten Null ⇒ erste Nullstelle des ${\rm si}$–Spektrums bei $4 \cdot f_{\rm A}= 250\text{ Hz}$. | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(17)''' Neue Einstellung: $\text{IDFT von Spektrum (L): Gaußspektrum}$. Interpretieren Sie das Ergebnis im Zeitbereich.}} | ||
| + | |||
| + | ::* Die Zeitfunktion $x(t)$ ist hier ebenfalls gaußförmig mit dem Maximum $x(t=0)=4$. Für das Spektrum gilt $X(f=0)=D(0)/f_{\rm A} = 16\cdot \text{ kHz}^{-1}$. | ||
| + | ::* Die äquivalente Impulsdauer ist $\Delta t= X(f= 0)/x(t= 0) = 4\text{ ms}$. Der Kehrwert ergibt die äquivalente Bandbreite $\Delta f = 1/\Delta t= 250\text{ Hz}$. | ||
| Line 229: | Line 404: | ||
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
<br> | <br> | ||
| − | [[File: | + | [[File:Anleitung_DFT_endgültig.png|left|600px]] |
| − | '''(A)''' | + | '''(A)''' Zeitbereich (Eingabe- und Ergebnisfeld) |
| − | '''(B)''' | + | '''(B)''' '''(A)'''–Darstellung numerisch, grafisch, Betrag |
| − | '''(C)''' | + | '''(C)''' Frequenzbereich (Eingabe- und Ergebnisfeld) |
| − | '''(D)''' | + | '''(D)''' '''(C)'''–Darstellung numerisch, grafisch, Betrag |
| − | '''(E)''' | + | '''(E)''' Auswahl: DFT $(t \to f)$ oder IDFT $(f \to t)$ |
| − | '''(F)''' | + | '''(F)''' Vorgegebene $d(\nu)$–Belegungen (falls DFT), oder |
| − | | + | Vorgegebene $D(\mu)$–Belegungen (falls IDFT) |
| − | '''( | + | '''(G)''' Eingabefeld auf Null setzen |
| − | '''( | + | '''(H)''' Eingabefeld zyklisch nach unten (bzw. oben) verschieben |
| − | '''( | + | '''( I )''' Bereich für die Versuchsdurchführung: Aufgabenauwahl |
| − | '''( | + | '''(J)''' Bereich für die Versuchsdurchführung: Aufgabenstellung |
| − | '''( | + | '''(K)''' Bereich für die Versuchsdurchführung: Musterlösung einblenden |
| − | |||
| − | |||
<br clear=all> | <br clear=all> | ||
| + | *Vorgegebene $d(\nu)$–Belegungen (für DFT): | ||
| + | |||
| + | :(a) entsprechend Zahlenfeld, (b) Gleichsignal, (c) Komplexe Exponentialfunktion der Zeit, (d) Harmonische Schwingung $($Phase $\varphi = 45^\circ)$, | ||
| + | :(e) Cosinussignal (eine Periode), (f) Sinussignal (eine Periode), (g) Cosinussignal (zwei Perioden), (h) Alternierende Zeitkoeffizienten, | ||
| + | : (i) Diracimpuls, (j) Rechteckimpuls, (k) Dreieckimpuls, (l) Gaußimpuls. | ||
| + | |||
| + | *Vorgegebene $D(\mu)$–Belegungen (für IDFT): | ||
| + | |||
| + | :(A) entsprechend Zahlenfeld, (B) Konstantes Spektrum, (C) Komplexe Exponentialfunktion der Frequenz, (D) äquivalent zur Einstellung (d) im Zeitbereich , | ||
| + | :(E) Cosinussignal (eine Frequenzperiode), (F) Sinussignal (eine Frequenzperiode), (G) Cosinussignal (zwei Frequenzperioden), (H) Alternierende Spektralkoeffizienten, | ||
| + | :(I) Diracspektrum, (J) Rechteckspektrum, (K) Dreieckspektrum, (L) Gaußspektrum. | ||
| + | |||
==Über die Autoren== | ==Über die Autoren== | ||
| − | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | + | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. |
| − | *Die erste Version wurde 2003 von [[ | + | *Die erste Version wurde 2003 von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Thomas_Gro.C3.9Fer_.28Diplomarbeit_LB_2006.2C_danach_freie_Mitarbeit_bis_2010.29|Thomas Großer]] im Rahmen ihrer Diplomarbeit mit "FlashMX–Actionscript" erstellt (Betreuer: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | * 2019 wurde das Programm von [[ | + | * 2019 wurde das Programm von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] im Rahmen einer Werkstudententätigkeit auf "HTML5" umgesetzt und neu gestaltet (Betreuer: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]]). |
| Line 269: | Line 454: | ||
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|dft}} |
Latest revision as of 15:44, 28 May 2021
Contents
- 1 Programmbeschreibung
- 2 Theoretischer Hintergrund
- 2.1 Argumente für die diskrete Realisierung der Fouriertransformation
- 2.2 Zeitdiskretisierung – Periodifizierung im Frequenzbereich
- 2.3 Frequenzdiskretisierung – Periodifizierung im Zeitbereich
- 2.4 Finite Signaldarstellung
- 2.5 Diskrete Fouriertransformation
- 2.6 Inverse Diskrete Fouriertransformation
- 2.7 Interpretation von DFT und IDFT
- 3 Versuchsdurchführung
- 4 Zur Handhabung des Applets
- 5 Über die Autoren
- 6 Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
Programmbeschreibung
Das Applet verdeutlicht die Eigenschaften zweidimensionaler Gaußscher Zufallsgrößen $XY\hspace{-0.1cm}$, gekennzeichnet durch die Standardabweichungen (Streuungen) $\sigma_X$ und $\sigma_Y$ ihrer beiden Komponenten sowie den Korrelationskoeffizienten $\rho_{XY}$ zwischen diesen. Die Komponenten werden als mittelwertfrei vorausgesetzt: $m_X = m_Y = 0$.
Das Applet zeigt
- die zweidimensionale Wahrscheinlichkeitsdichtefunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{XY}(x, \hspace{0.1cm}y)$ in dreidimensionaler Darstellung sowie in Form von Höhenlinien,
- die zugehörige Randwahrscheinlichkeitsdichtefunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}WDF$ $f_{X}(x)$ der Zufallsgröße $X$ als blaue Kurve; ebenso $f_{Y}(y)$ für die zweite Zufallsgröße,
- die zweidimensionale Verteilungsfunktion ⇒ $\rm 2D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{XY}(x, \hspace{0.1cm}y)$ als 3D-Plot,
- die Verteilungsfunktion ⇒ $\rm 1D\hspace{-0.1cm}-\hspace{-0.1cm}VTF$ $F_{X}(x)$ der Zufallsgröße $X$; ebenso $F_{Y}(y)$ als rote Kurve.
Das Applet verwendet das Framework Plot.ly
Theoretischer Hintergrund
Argumente für die diskrete Realisierung der Fouriertransformation
Die Fouriertransformation gemäß der herkömmlichen Beschreibung für zeitkontinuierliche Signale weist aufgrund der unbegrenzten Ausdehnung des Integrationsintervalls eine unendlich hohe Selektivität auf und ist deshalb ein ideales theoretisches Hilfsmittel der Spektralanalyse.
Sollen die Spektralanteile $X(f)$ einer Zeitfunktion $x(t)$ numerisch ermittelt werden, so sind die allgemeinen Transformationsgleichungen
- $$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Hintransformation}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{Erstes Fourierintegral} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} \text{Rücktransformation}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{Zweites Fourierintegral} \hspace{0.05cm}\end{align*}$$
aus zwei Gründen ungeeignet:
- Die Gleichungen gelten ausschließlich für zeitkontinuierliche Signale. Mit Digitalrechnern oder Signalprozessoren kann man jedoch nur zeitdiskrete Signale verarbeiten.
- Für eine numerische Auswertung der beiden Fourierintegrale ist es erforderlich, das jeweilige Integrationsintervall auf einen endlichen Wert zu begrenzen.
$\text{Daraus ergibt sich folgende Konsequenz:}$
Ein kontinuierliches Signal muss vor der numerischen Bestimmung seiner Spektraleigenschaften zwei Prozesse durchlaufen, nämlich
- den der Abtastung zur Diskretisierung, und
- den der Fensterung zur Begrenzung des Integrationsintervalls.
Im Folgenden wird ausgehend von einer aperiodischen Zeitfunktion $x(t)$ und dem dazugehörigen Fourierspektrum $X(f)$ eine für die Rechnerverarbeitung geeignete zeit– und frequenzdiskrete Beschreibung vorgestellt.
Zeitdiskretisierung – Periodifizierung im Frequenzbereich
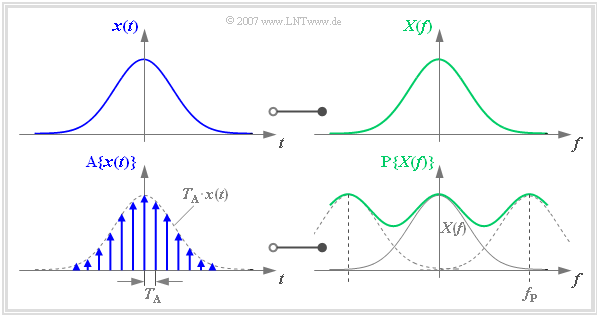
Die folgenden Grafiken zeigen einheitlich links den Zeitbereich und rechts den Frequenzbereich. Ohne Einschränkung der Allgemeingültigkeit sind $x(t)$ und $X(f)$ jeweils reell und gaußförmig.
Man kann die Abtastung des Zeitsignals $x(t)$ durch die Multiplikation mit einem Diracpuls $p_{\delta}(t)$ beschreiben. Es ergibt sich das im Abstand $T_{\rm A}$ abgetastete Zeitsignal
- $${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
Dieses abgetastete Signal $\text{A}\{ x(t)\}$ transformieren wir nun in den Frequenzbereich. Der Multiplikation des Diracpulses $p_{\delta}(t)$ mit $x(t)$ entspricht im Frequenzbereich die Faltung von $P_{\delta}(f)$ mit $X(f)$. Es ergibt sich das periodifizierte Spektrum $\text{P}\{ X(f)\}$, wobei $f_{\rm P}$ die Frequenzperiode der Funktion $\text{P}\{ X(f)\}$ angibt:
- $${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} )\hspace{0.5cm} {\rm mit }\hspace{0.5cm}f_{\rm P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$
- Das abgetastete Signal nennen wir $\text{A}\{ x(t)\}$.
- Die Frequenzperiode wird mit $f_{\rm P}$ = $1/T_{\rm A}$ bezeichnet.
Die obige Grafik zeigt den hier beschriebenen Funktionalzusammenhang. Es ist anzumerken:
- Die Frequenzperiode $f_{\rm P}$ wurde hier bewusst klein gewählt, so dass die Überlappung der zu summierenden Spektren deutlich zu erkennen ist.
- In der Praxis sollte $f_{\rm P}$ aufgrund des Abtasttheorems mindestens doppelt so groß sein wie die größte im Signal $x(t)$ enthaltene Frequenz.
- Ist dies nicht erfüllt, so muss mit Aliasing gerechnet werden.
Frequenzdiskretisierung – Periodifizierung im Zeitbereich
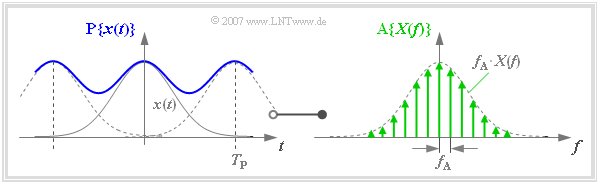
Die Diskretisierung von $X(f)$ lässt sich ebenfalls durch eine Multiplikation mit einem Diracpuls beschreiben. Es ergibt sich das im Abstand $f_{\rm A}$ abgetastete Spektrum:
- $${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$
Transformiert man den hier verwendeten Frequenz–Diracpuls $($mit Impulsgewichten $f_{\rm A})$ in den Zeitbereich, so erhält man mit $T_{\rm P} = 1/f_{\rm A}$:
- $$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
Die Multiplikation mit $X(f)$ entspricht im Zeitbereich der Faltung mit $x(t)$. Man erhält das im Abstand $T_{\rm P}$ periodifizierte Signal $\text{P}\{ x(t)\}$:
- $${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
$\text{Beispiel 1:}$ Dieser Zusammenhang ist in der Grafik veranschaulicht:
- Aufgrund der groben Frequenzrasterung ergibt sich in diesem Beispiel für die Zeitperiode $T_{\rm P}$ ein relativ kleiner Wert.
- Deshalb unterscheidet sich das (blaue) periodifizierte Zeitsignal $\text{P}\{ x(t)\}$ aufgrund von Überlappungen deutlich von $x(t)$.
Finite Signaldarstellung
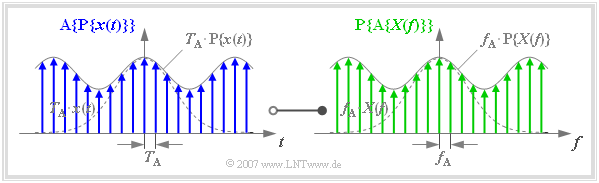
Zur so genannten finiten Signaldarstellung kommt man,
- wenn sowohl die Zeitfunktion $x(t)$
- als auch die Spektralfunktion $X(f)$
ausschließlich durch ihre Abtastwerte angegeben werden.
Die Grafik ist wie folgt zu interpretieren:
- Im linken Bild blau eingezeichnet ist die Funktion $\text{A}\{ \text{P}\{ x(t)\}\}$. Diese ergibt sich durch Abtastung der periodifizierten Zeitfunktion $\text{P}\{ x(t)\}$ mit äquidistanten Diracimpulsen im Abstand $T_{\rm A} = 1/f_{\rm P}$.
- Im rechten Bild grün eingezeichnet ist die Funktion $\text{P}\{ \text{A}\{ X(f)\}\}$. Diese ergibt sich durch Periodifizierung $($mit $f_{\rm P})$ der abgetasteten Spektralfunktion $\{ \text{A}\{ X(f)\}\}$.
- Zwischen dem blauen finiten Signal und dem grünen finiten Signal besteht ebenfalls eine Fourierkorrespondenz, und zwar die folgende:
- $${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$
Die Diraclinien der periodischen Fortsetzung $\text{P}\{ \text{A}\{ X(f)\}\}$ der abgetasteten Spektralfunktion fallen allerdings nur dann in das gleiche Frequenzraster wie diejenigen von $\text{A}\{ X(f)\}$, wenn die Frequenzperiode $f_{\rm P}$ ein ganzzahliges Vielfaches $(N)$ des Frequenzabtastabstandes $f_{\rm A}$ ist.
- Bei Anwendung der finiten Signaldarstellung muss stets die folgende Bedingung erfüllt sein, wobei für die natürliche Zahl $N$ in der Praxis meist eine Zweierpotenz verwendet wird (der obigen Grafik liegt der Wert $N = 8$ zugrunde):
- $$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A} }= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$
Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt:
- $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$
$\text{Fazit:}$
- Die Zeitfunktion $\text{P}\{ \text{A}\{ x(t)\}\}$ besitzt die Periode $T_{\rm P} = N \cdot T_{\rm A}$.
- Die Periode im Frequenzbereich ist $f_{\rm P} = N \cdot f_{\rm A}$.
- Zur Beschreibung des diskretisierten Zeit– und Frequenzverlaufs reichen somit jeweils $N$ komplexe Zahlenwerte in Form von Impulsgewichten aus.
$\text{Beispiel 2:}$ Es liegt ein zeitbegrenztes (impulsartiges) Signal $x(t)$ in abgetasteter Form vor, wobei der Abstand zweier Abtastwerte $T_{\rm A} = 1\, {\rm µ s}$ beträgt:
- Nach einer diskreten Fouriertransformation mit $N = 512$ liegt das Spektrum $X(f)$ in Form von Abtastwerten im Abstand $f_{\rm A} = (N \cdot T_{\rm A})^{–1} \approx 1.953\,\text{kHz} $ vor.
- Vergrößert man den DFT–Parameter auf $N= 2048$, so ergibt sich ein feineres Frequenzraster mit $f_{\rm A} \approx 488\,\text{Hz}$.
Diskrete Fouriertransformation
Aus dem herkömmlichen "ersten Fourierintegral"
- $$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion
- $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind.
Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor:
- Die $N$ Zeitbereichskoeffizienten seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Die $N$ Frequenzbereichskoeffizienten seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1:
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abkürzend wird für den von $N$ abhängigen komplexen Drehfaktor geschrieben:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
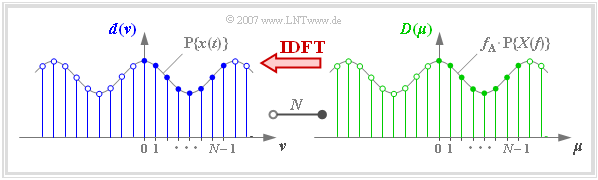
$\text{Definition:}$
Unter dem Begriff Diskrete Fouriertransformation (kurz DFT) versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
In der Grafik erkennt man an einem Beispiel
- die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung,
- die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.
Inverse Diskrete Fouriertransformation
Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das "zweite Fourierintegral"
- $$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in diskretisierter Form: $d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$
$\text{Definition:}$
Unter dem Begriff Inverse Diskrete Fouriertransformation (kurz IDFT) versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier:
- $$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$
- $$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$
- $$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$
Ein Vergleich zwischen DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind:
- Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen.
- Bei der IDFT entfällt die Division durch $N$.
Interpretation von DFT und IDFT
Die Grafik zeigt die diskreten Koeffizienten im Zeit– und Frequenzbereich zusammen mit den periodifizierten zeitkontinuierlichen Funktionen.
Bei Anwendung von DFT bzw. IDFT ist zu beachten:
- Nach obigen Definitionen besitzen die DFT–Koeffizienten $d(ν)$ und $D(\mu)$ stets die Einheit der Zeitfunktion.
- Dividiert man $D(\mu)$ durch $f_{\rm A}$, so erhält man den Spektralwert $X(\mu \cdot f_{\rm A})$.
- Die Spektralkoeffizienten $D(\mu)$ müssen stets komplex angesetzt werden, um auch ungerade Zeitfunktionen berücksichtigen zu können.
- Um auch Bandpass–Signale im äquivalenten Tiefpass–Bereich transformieren zu können, verwendet man meist auch komplexe Zeitkoeffizienten $d(\nu)$.
- Als Grundintervall für $\nu$ und $\mu$ definiert man meist – wie in obiger Grafik – den Bereich von $0$ bis $N - 1$.
- Mit den komplexwertigen Zahlenfolgen $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.1cm}\rangle$ sowie $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.1cm}\rangle$ werden DFT und IDFT ähnlich wie die herkömmliche Fouriertransformation symbolisiert:
- $$\langle \hspace{0.1cm} D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$
- Ist die Zeitfunktion $x(t)$ bereits auf den Bereich $0 \le t \lt N \cdot T_{\rm A}$ begrenzt, dann geben die von der IDFT ausgegebenen Zeitkoeffizienten direkt die Abtastwerte der Zeitfunktion an: $d(\nu) = x(\nu \cdot T_{\rm A}).$
- Ist $x(t)$ gegenüber dem Grundintervall verschoben, so muss man die im $\text{Beispiel 3}$ gezeigte Zuordnung zwischen $x(t)$ und den Koeffizienten $d(\nu)$ wählen.
$\text{Beispiel 3:}$ Die obere Grafik zeigt den unsymmetrischen Dreieckimpuls $x(t)$, dessen absolute Breite kleiner ist als $T_{\rm P} = N \cdot T_{\rm A}$.
Die untere Skizze zeigt die zugeordneten DFT–Koeffizienten gültig für $N = 8$
- Für $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$ gilt $d(\nu) = x(\nu \cdot T_{\rm A})$:
- $$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$
- $$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$
- Dagegen sind die Koeffizienten $d(5)$, $d(6)$ und d$(7)$ wie folgt zu setzen:
- $$d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ) $$
- $$ \Rightarrow \hspace{0.2cm}d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(7) = x (-T_{\rm A})\hspace{0.05cm}.$$
Versuchsdurchführung
- Wählen Sie zunächst die Nummer (1, ...) der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von "Musterlösung".
Die Nummer 0 entspricht einem "Reset":
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines "Reset–Textes" mit weiteren Erläuterungen zum Applet.
(1) Neue Einstellung: $\text{DFT von Signal (b): Gleichsignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen $\text{FT}$ ?
- Im Zeitbereich sind alle $d(\nu) =1$. Im Frequenzbereich sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(0)] =1$.
- Dies entspricht bei der herkömmlichen (zeitkontinuierlichen) Fouriertransformation: $x(t) = A\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = A \cdot \delta(f=0)$ mit $A=1$.
(2) Gehen Sie vom erhaltenen $D(\mu)$–Feld aus und verschieben Sie alle Koeffizienten um eine Stelle nach unten. Welche Zeitfunktion liefert die $\rm IDFT$?
- Nun sind alle $D(\mu) =0$ mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Das Zeitbereichsergebnis ist eine komplexe Exponentialfunktion.
- Der Realteil des $d(\nu)$–Feldes zeigt einen Cosinus und der Imaginärteil eine Sinusfunktion. Bei beiden Funktionen erkennt man jeweils eine Periode.
(3) Ergänzen Sie das aktuelle $D(\mu)$–Feld um den Koeffizienten ${\rm Im}\big [D(1)] =1$. Welche Unterschiede erkennt man gegenüber (2) im Zeitbereich?
- Zum einen erkennt man nun bei Realteil und Imaginärteil eine Phasenverschiebung um zwei Stützwerte. Dies entspricht der Phase $\varphi = 45^\circ$.
- Zudem wurden die Amplituden von Real– und Imaginärteil jeweils um den Faktor $\sqrt{2}$ vergrößert.
(4) Setzen Sie das $D(\mu)$–Feld auf Null mit Ausnahme von ${\rm Re}\big [D(1)] =1$. Durch welchen zusätzlichen $D(\mu)$–Koeffizienten erhält man ein reelles $d(\nu)$–Feld?
- Durch Probieren oder Nachdenken erkennt man, dass auch ${\rm Re}\big [D(15)] =1$ gesetzt werden muss. Dann beschreibt das $d(\nu)$–Feld einen Cosinus.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = 2 \cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = \delta(f -f_0)+\delta(f +f_0)$.
- Das Feld $D(1)$ steht für die Frequenz $+f_0$ und aufgrund der Periodizät mit $N=16$ wird die Frequenz $-f_0$ durch $D(15) = D(-1)$ ausgedrückt.
(5) Mit welchem $D(\mu)$–Feld erhält man nach der $\rm IDFT$ im $d(\nu)$–Feld eine reelle Cosinusfunktion mit der Amplitude $A=1$?
- Die Diskrete Fouriertransformation ist ebenso wie die herkömmliche Fouriertransformation linear ⇒ $D(1) = D(15)=0.5$.
(6) Neue Einstellung: $\text{DFT von Signal (e): Cosinussignal}$ und anschließende Signalverschiebungen. Was bewirken diese Verschiebungen im Frequenzbereich?
- Eine Verschiebung im Zeitbereich verändert das Cosinussignal zu einer "Harmonischen Schwingung" mit beliebiger Phase.
- Das $D(\mu)$–Feld ist weiterhin Null bis auf $D(1)$ und $D(15)$. Die Beträge $|D(1)|$ und $|D(15)|$ bleiben ebenfalls gleich.
- Die alleinige Veränderung betrifft die Phase, also die unterschiedliche Aufteilung der Beträge auf Real– und Imaginärteil.
(7) Neue Einstellung: $\text{DFT von Signal (f): Sinussignal}$. Interpretieren Sie das Ergebnis im Frequenzbereich. Wie lautet das Analogon der herkömmlichen $\text{FT}$ ?
- Das Sinussignal ergibt sich aus dem Cosinussignal durch vier Zeitverschiebungen. Deshalb gelten alle Aussagen von (6) weiterhin.
- Für die herkömmliche (zeitkontinuierliche) Fouriertransformation gilt: $x(t) = \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = {\rm j}/2 \cdot \big [\delta(f +f_0)-\delta(f -f_0)\big ]$.
- Der Koeffizient $D(1)$ ⇒ $($Frequenz: $+f_0)$ ist imaginär und hat den Imaginärteil $-0.5$. Entsprechend gilt ${\rm Im}\big [D(15)] =+0.5$ ⇒ $($Frequenz: $-f_0)$.
(8) Neue Einstellung: $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$. Interpretieren Sie das Ergebnis im Vergleich zur Aufgabe (5).
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (2f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -2 f_0)+0.5 \cdot \delta(f +2f_0)$.
- Für die Frequenz $2f_0$ steht das Feld $D(2)$ und für die Frequenz $-2f_0$ aufgrund der Periodizät das Feld $D(14) = D(-2)$ : $D(2) = D(14) = 0.5$.
(9) Untersuchen Sie nun den Fall $\text{DFT von Sinussignal (zwei Perioden)}$. Welche Einstellung müssen Sie vornehmen? Interpretieren Sie das Ergebnis.
- Zum gewünschten Signal kommt man von $\text{DFT von Signal (g): Cosinussignal (zwei Perioden)}$ mit zwei Verschiebungen. Bei (7): Vier Verschiebungen.
- Das DFT–Ergebnis lautet dementsprechend: ${\rm Im}\big [D(2)] =-0.5$ und ${\rm Im}\big [D(14)] =+0.5$.
(10) Neue Einstellung: $\text{DFT von (h) Alternierende Zeitkoeffizienten}$. Interpretieren Sie das DFT–Ergebnis.
- Hier lautet die zeitkontinuierliche Fouriertransformation: $x(t) = \cos(2\pi \cdot (8f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f) = 0.5 \cdot \delta(f -8 f_0)+0.5 \cdot \delta(f +8f_0)$.
- $8f_0$ ist die höchste mit $N=16$ in der DFT darstellbare Frequenz. Pro Periodendauer gibt es nur zwei Abtastwerte, nämlich $+1$ und $-1$.
- Unterschied zur Teilaufgabe (5): Aus $D(1) =0.5$ wird nun $D(8) =0.5$. Ebenso verschiebt sich $D(15) =0.5$ auf $D(8) =0.5$. Endergebnis: $D(8) =1$.
(11) Welche Unterschiede erhält man mit den beiden Einstellungen $\text{DFT von Signal (i): Diracimpuls}$ sowie $\text{IDFT von Spektrum (I): Diracspektrum}$ ?
- Keine! Im ersten Fall sind alle Koeffizienten $D(\mu) = 1$ (reell); im zweiten Fall dagegen in äquivalenter Weise die Koeffizienten $d(\nu) = 1$ (reell).
(12) Gibt es Unterschiede, wenn man im jeweiligen Eingabefeld die reelle $1$ um jeweils eine Stelle nach unten verschiebt, also $d(\nu=1) = 1$ bzw. $D(\mu=1) = 1$?
- Im ersten Fall ⇒ ${\rm Re}\big [d(\nu=1)] = 1$ ergibt sich im Frequenzbereich die komplexe Exponentialfunktion ⇒ $X(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ mit negativem Vorzeichen.
- Im zweiten Fall ⇒ ${\rm Re}\big [D(\mu=1)] = 1$ ergibt sich im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit positivem Vorzeichen.
- Hinweis: Mit ${\rm Re}\big [D(\mu=15)] = 1$ ergäbe sich auch im Zeitbereich die komplexe Exponentialfunktion ⇒ $x(t) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}2\pi \hspace{0.05cm}\cdot\hspace{0.05cm} f_0 \hspace{0.05cm}\cdot\hspace{0.05cm} t}$ mit negativem Vorzeichen.
(13) Neue Einstellung: $\text{DFT von Signal (k): Dreieckimpuls}$. Interpretieren Sie die $d(\nu)$–Belegungunter der Annahme $T_{\rm A} = 1 \ \rm ms$.
- Wählen Sie die Betragsdarstellung. $x(t)$ ist symmetrisch um $t=0$ und erstreckt sich von $-8 \cdot T_{\rm A} = -8 \ \rm ms$ bis $+8 \cdot T_{\rm A} = +8 \ \rm ms$.
- $d(\nu)$–Belegung: $d(0)=x(0)= 1$, $d(1)=x(T_{\rm A})= 0.875$, ... , $d(8)=x(8T_{\rm A})= 0$, $d(9)=x(-7T_{\rm A})= 0.125$, ..., $d(15)=x(-T_{\rm A})= 0.875$.
(14) Gleiche Einstellung wie bei (13). Interpretieren Sie das DFT–Ergebnis, insbesondere die Koeffizienten $D(0)$, $D(1)$, $D(2)$ und $D(15)$.
- Im Frequenzbereich steht $D(0)$ für die Frequenz $f= 0$ und $D(1)$ und $D(15)$ für die Frequenzen $\pm f_{\rm A}$. Es gilt $f_{\rm A} = 1/(N \cdot T_{\rm A}) = 62.5\text{ Hz}$.
- Für den Wert des kontinuierlichen Spektrums bei $f=0$ gilt $X(f=0)=D(0)/f_{\rm A} = 0.5/(0.0625\text{ kHz}) = 8\cdot \text{ kHz}^{-1}$.
- Die erste Nullstelle des ${\rm si}^2$–förmigen Spektrums $X(f)$ tritt bei $2 \cdot f_{\rm A}= 125\text{ Hz}$ auf. Die weiteren Nullstellen sind äquidistant.
(15) Neue Einstellung: $\text{DFT von Signal (i): Rechteckimpuls}$. Interpretieren Sie die dargestellten Ergebnisse.
- Das eingestellte (symmetrische) Rechteck erstreckt sich über $\pm 4 \cdot T_{\rm A}$. An den Rändern sind die Zeitkoeffizienten nur halb so groß: $d(4) = d(12) =0.5$.
- Die weiteren Aussagen von (14) gelten auch für dieses ${\rm si}$–förmige Spektrum $X(f)$.
(16) Gleiche Einstellung wie bei (15). Welche Modifikationen sind am $d(\nu)$–Feld vorzunehmen, um die Rechteckdauer zu halbieren ⇒ $\pm 2 \cdot T_{\rm A}$.
- $d(0) = d(1) = d(15) =1, \ d(2) = d(14) = 0.5$. Alle anderen Zeitkoeffizienten Null ⇒ erste Nullstelle des ${\rm si}$–Spektrums bei $4 \cdot f_{\rm A}= 250\text{ Hz}$.
(17) Neue Einstellung: $\text{IDFT von Spektrum (L): Gaußspektrum}$. Interpretieren Sie das Ergebnis im Zeitbereich.
- Die Zeitfunktion $x(t)$ ist hier ebenfalls gaußförmig mit dem Maximum $x(t=0)=4$. Für das Spektrum gilt $X(f=0)=D(0)/f_{\rm A} = 16\cdot \text{ kHz}^{-1}$.
- Die äquivalente Impulsdauer ist $\Delta t= X(f= 0)/x(t= 0) = 4\text{ ms}$. Der Kehrwert ergibt die äquivalente Bandbreite $\Delta f = 1/\Delta t= 250\text{ Hz}$.
Zur Handhabung des Applets
(A) Zeitbereich (Eingabe- und Ergebnisfeld)
(B) (A)–Darstellung numerisch, grafisch, Betrag
(C) Frequenzbereich (Eingabe- und Ergebnisfeld)
(D) (C)–Darstellung numerisch, grafisch, Betrag
(E) Auswahl: DFT $(t \to f)$ oder IDFT $(f \to t)$
(F) Vorgegebene $d(\nu)$–Belegungen (falls DFT), oder
Vorgegebene $D(\mu)$–Belegungen (falls IDFT)
(G) Eingabefeld auf Null setzen
(H) Eingabefeld zyklisch nach unten (bzw. oben) verschieben
( I ) Bereich für die Versuchsdurchführung: Aufgabenauwahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
(K) Bereich für die Versuchsdurchführung: Musterlösung einblenden
- Vorgegebene $d(\nu)$–Belegungen (für DFT):
- (a) entsprechend Zahlenfeld, (b) Gleichsignal, (c) Komplexe Exponentialfunktion der Zeit, (d) Harmonische Schwingung $($Phase $\varphi = 45^\circ)$,
- (e) Cosinussignal (eine Periode), (f) Sinussignal (eine Periode), (g) Cosinussignal (zwei Perioden), (h) Alternierende Zeitkoeffizienten,
- (i) Diracimpuls, (j) Rechteckimpuls, (k) Dreieckimpuls, (l) Gaußimpuls.
- Vorgegebene $D(\mu)$–Belegungen (für IDFT):
- (A) entsprechend Zahlenfeld, (B) Konstantes Spektrum, (C) Komplexe Exponentialfunktion der Frequenz, (D) äquivalent zur Einstellung (d) im Zeitbereich ,
- (E) Cosinussignal (eine Frequenzperiode), (F) Sinussignal (eine Frequenzperiode), (G) Cosinussignal (zwei Frequenzperioden), (H) Alternierende Spektralkoeffizienten,
- (I) Diracspektrum, (J) Rechteckspektrum, (K) Dreieckspektrum, (L) Gaußspektrum.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2003 von Thomas Großer im Rahmen ihrer Diplomarbeit mit "FlashMX–Actionscript" erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf "HTML5" umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.