Difference between revisions of "Aufgaben:Exercise 1.7: Ternary Markov Chain"
From LNTwww
| (6 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Markov_Chains |
}} | }} | ||
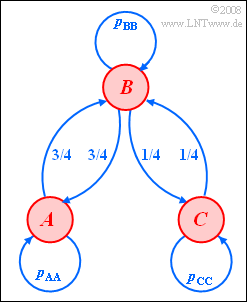
| − | [[File:P_ID453__Sto_A_1_7.png|right|frame| | + | [[File:P_ID453__Sto_A_1_7.png|right|frame|Ternary Markov chain]] |
| − | + | We consider a Markov chain with three possible events $A$, $B$, $C$: | |
| − | * | + | *The transition probabilities are shown in the graph. |
| − | * | + | *Thus, a transition from $A$ to $C$ and vice versa is not possible. |
:$$p_\text{AC} = p_\text{CA} = 0.$$ | :$$p_\text{AC} = p_\text{CA} = 0.$$ | ||
| − | + | The three event probabilities at the starting time $(\nu = 0)$ are given as follows: | |
:$${\rm Pr}(A_0) = 0,$$ | :$${\rm Pr}(A_0) = 0,$$ | ||
| − | |||
:$${\rm Pr}(B_0) = 1,$$ | :$${\rm Pr}(B_0) = 1,$$ | ||
| − | |||
:$${\rm Pr}(C_0) = 0.$$ | :$${\rm Pr}(C_0) = 0.$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Markov_Chains|Markov Chains]]. |
| − | * | + | *In particular, reference is made to the page [[Theory_of_Stochastic_Signals/Markov_Chains#Matrix_vector_representation|Matrix vector representation]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Give the transition matrix ${\mathbf{P}}$ and the transition probabilities $p_\text{AA}$, $p_\text{BB}$ and $p_\text{CC}$. |
|type="{}"} | |type="{}"} | ||
$p_\text{AA} \ = \ $ { 0.25 3% } | $p_\text{AA} \ = \ $ { 0.25 3% } | ||
| Line 39: | Line 34: | ||
$p_\text{CC} \ = \ $ { 0.75 3% } | $p_\text{CC} \ = \ $ { 0.75 3% } | ||
| − | { | + | {Calculate the event probabilities at time $\nu = 1$, in particular |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(A_1) \ = \ $ { 0.75 3% } | ${\rm Pr}(A_1) \ = \ $ { 0.75 3% } | ||
| − | { | + | {Calculate the event probabilities at time $\nu = 2$, in particular |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(A_2) \ = \ ${ 0.1875 3% } | ${\rm Pr}(A_2) \ = \ ${ 0.1875 3% } | ||
| − | { | + | {What probabilities will occur very long after the Markov chain is turned on $(ν \rightarrow \infty)$? <br>In particular, what is the ergodic probability ${\rm Pr}(A)$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(A) \ = \ $ { 0.333 3% } | ${\rm Pr}(A) \ = \ $ { 0.333 3% } | ||
| Line 56: | Line 51: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' In general (or in this special case) it must hold: |
:$$p_{\rm AA} = 1 - p_{\rm AB} - p_{\rm AC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm AA} = 1 - 0.75 -0 \hspace{0.15cm}\underline {= 0.25},$$ | :$$p_{\rm AA} = 1 - p_{\rm AB} - p_{\rm AC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm AA} = 1 - 0.75 -0 \hspace{0.15cm}\underline {= 0.25},$$ | ||
:$$p_{\rm BB} = 1 - p_{\rm BA} - p_{\rm BC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm BB} = 1 - 0.75 -0.25 \hspace{0.15cm}\underline {= 0},$$ | :$$p_{\rm BB} = 1 - p_{\rm BA} - p_{\rm BC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm BB} = 1 - 0.75 -0.25 \hspace{0.15cm}\underline {= 0},$$ | ||
:$$p_{\rm CC} = 1 - p_{\rm CA} - p_{\rm CB} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm CC} = 1 - 0 - 0.25 \hspace{0.15cm}\underline {= 0.75}.$$ | :$$p_{\rm CC} = 1 - p_{\rm CA} - p_{\rm CB} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm CC} = 1 - 0 - 0.25 \hspace{0.15cm}\underline {= 0.75}.$$ | ||
| − | * | + | *Thus, the transition matrix is: |
:$${\mathbf{P}} = \left[ \begin{array}{ccc} 1/4 & 3/4 & 0 \\ 3/4 & 0 & 1/4 \\ 0 & 1/4 & 3/4 \end{array} \right] .$$ | :$${\mathbf{P}} = \left[ \begin{array}{ccc} 1/4 & 3/4 & 0 \\ 3/4 & 0 & 1/4 \\ 0 & 1/4 & 3/4 \end{array} \right] .$$ | ||
| − | '''(2)''' | + | '''(2)''' Because of ${\rm Pr}(B_0) = 1$ and $p_\text{BB} = 0$, at time $\nu = 1$ the event $B$ cannot occur and $A$ is much more probable than $C$: |
:$$\hspace{0.15cm}\underline {{\rm Pr}(A_1) = 0.75}; \hspace{0.5cm} {\rm Pr}(B_1) = 0; \hspace{0.5cm}{\rm Pr}(C_1) = 0.25.$$ | :$$\hspace{0.15cm}\underline {{\rm Pr}(A_1) = 0.75}; \hspace{0.5cm} {\rm Pr}(B_1) = 0; \hspace{0.5cm}{\rm Pr}(C_1) = 0.25.$$ | ||
| − | * | + | *The same result is obtained by applying the vector matrix representation. |
| − | '''(3)''' | + | '''(3)''' For the probability vector at time $\nu = 2$ holds: |
:$${\mathbf{p}^{(\nu = 2)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu =1 )}}= \left[ \begin{array}{ccc} 1/4 & 3/4& 0 \\ 3/4 & 0 & 1/4 \\ 0& 1/4& 3/4 \end{array} \right] \left[ \begin{array}{c} 3/4 \\ 0 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 3/16 \\ 10/16 \\ 3/16 \end{array} \right] .$$ | :$${\mathbf{p}^{(\nu = 2)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu =1 )}}= \left[ \begin{array}{ccc} 1/4 & 3/4& 0 \\ 3/4 & 0 & 1/4 \\ 0& 1/4& 3/4 \end{array} \right] \left[ \begin{array}{c} 3/4 \\ 0 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 3/16 \\ 10/16 \\ 3/16 \end{array} \right] .$$ | ||
| − | * | + | *Thus, the event probability is ${\rm Pr}(A_2) = 3/16\hspace{0.15cm}\underline {= 0.1875}$. |
| − | '''(4)''' | + | '''(4)''' To solve this problem, several possibilities should be given. |
| − | * | + | *One is to solve a system of equations with three unknowns: |
:$${\rm Pr}(A) = 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B),$$ | :$${\rm Pr}(A) = 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B),$$ | ||
:$${\rm Pr}(B) = 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{2.8cm} + \hspace{0.1cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C),$$ | :$${\rm Pr}(B) = 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{2.8cm} + \hspace{0.1cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C),$$ | ||
:$${\rm Pr}(C) = \hspace{2.8cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C).$$ | :$${\rm Pr}(C) = \hspace{2.8cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C).$$ | ||
| − | : | + | :From the first equation we get ${\rm Pr}(B) = {\rm Pr}(A)$, from the last ${\rm Pr}(C) = {\rm Pr}(A)$. Since the sum of all probabilities is equal to $1$, it follows |
| − | * | + | :$$ {\rm Pr}(A) = {\rm Pr}(B) = {\rm Pr}(C) = 1/3 \hspace{0.15cm}\underline {\approx 0.333}.$$ |
| + | *The same result is obtained by analyzing the transition matrix. Since the sum of each column equals $1$ $($that is, the sum of each row of the transposed matrix also equals $1)$, it is obvious that all event probabilities must be equal. | ||
| − | * | + | *Even by thinking about it briefly, one could have predicted the result without calculating. Since at each event the numerical values at the outgoing arrows (only to other events) are equal with those at the incoming ones, it is not to be seen why one of the events should be preferred. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.4 Markov Chains |
^]] | ^]] | ||
Latest revision as of 14:21, 2 December 2021
We consider a Markov chain with three possible events $A$, $B$, $C$:
- The transition probabilities are shown in the graph.
- Thus, a transition from $A$ to $C$ and vice versa is not possible.
- $$p_\text{AC} = p_\text{CA} = 0.$$
The three event probabilities at the starting time $(\nu = 0)$ are given as follows:
- $${\rm Pr}(A_0) = 0,$$
- $${\rm Pr}(B_0) = 1,$$
- $${\rm Pr}(C_0) = 0.$$
Hints:
- The exercise belongs to the chapter Markov Chains.
- In particular, reference is made to the page Matrix vector representation.
Questions
Solution
(1) In general (or in this special case) it must hold:
- $$p_{\rm AA} = 1 - p_{\rm AB} - p_{\rm AC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm AA} = 1 - 0.75 -0 \hspace{0.15cm}\underline {= 0.25},$$
- $$p_{\rm BB} = 1 - p_{\rm BA} - p_{\rm BC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm BB} = 1 - 0.75 -0.25 \hspace{0.15cm}\underline {= 0},$$
- $$p_{\rm CC} = 1 - p_{\rm CA} - p_{\rm CB} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm CC} = 1 - 0 - 0.25 \hspace{0.15cm}\underline {= 0.75}.$$
- Thus, the transition matrix is:
- $${\mathbf{P}} = \left[ \begin{array}{ccc} 1/4 & 3/4 & 0 \\ 3/4 & 0 & 1/4 \\ 0 & 1/4 & 3/4 \end{array} \right] .$$
(2) Because of ${\rm Pr}(B_0) = 1$ and $p_\text{BB} = 0$, at time $\nu = 1$ the event $B$ cannot occur and $A$ is much more probable than $C$:
- $$\hspace{0.15cm}\underline {{\rm Pr}(A_1) = 0.75}; \hspace{0.5cm} {\rm Pr}(B_1) = 0; \hspace{0.5cm}{\rm Pr}(C_1) = 0.25.$$
- The same result is obtained by applying the vector matrix representation.
(3) For the probability vector at time $\nu = 2$ holds:
- $${\mathbf{p}^{(\nu = 2)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu =1 )}}= \left[ \begin{array}{ccc} 1/4 & 3/4& 0 \\ 3/4 & 0 & 1/4 \\ 0& 1/4& 3/4 \end{array} \right] \left[ \begin{array}{c} 3/4 \\ 0 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 3/16 \\ 10/16 \\ 3/16 \end{array} \right] .$$
- Thus, the event probability is ${\rm Pr}(A_2) = 3/16\hspace{0.15cm}\underline {= 0.1875}$.
(4) To solve this problem, several possibilities should be given.
- One is to solve a system of equations with three unknowns:
- $${\rm Pr}(A) = 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B),$$
- $${\rm Pr}(B) = 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{2.8cm} + \hspace{0.1cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C),$$
- $${\rm Pr}(C) = \hspace{2.8cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C).$$
- From the first equation we get ${\rm Pr}(B) = {\rm Pr}(A)$, from the last ${\rm Pr}(C) = {\rm Pr}(A)$. Since the sum of all probabilities is equal to $1$, it follows
- $$ {\rm Pr}(A) = {\rm Pr}(B) = {\rm Pr}(C) = 1/3 \hspace{0.15cm}\underline {\approx 0.333}.$$
- The same result is obtained by analyzing the transition matrix. Since the sum of each column equals $1$ $($that is, the sum of each row of the transposed matrix also equals $1)$, it is obvious that all event probabilities must be equal.
- Even by thinking about it briefly, one could have predicted the result without calculating. Since at each event the numerical values at the outgoing arrows (only to other events) are equal with those at the incoming ones, it is not to be seen why one of the events should be preferred.