Difference between revisions of "Aufgaben:Exercise 1.6Z: Ternary Markov Source"
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Discrete_Sources_with_Memory |
}} | }} | ||
| − | [[File:Inf_Z_1_6_vers2.png|right|frame| | + | [[File:Inf_Z_1_6_vers2.png|right|frame|Ternary Markov source]] |
| − | + | The diagram on the right shows a Markov source with $M = 3$ states $\rm A$, $\rm B$ and $\rm C$. | |
| − | + | Let the two parameters of this Markov process be: | |
:$$0 \le p \le 0.5 \hspace{0.05cm},\hspace{0.2cm}0 \le q \le 1 \hspace{0.05cm}.$$ | :$$0 \le p \le 0.5 \hspace{0.05cm},\hspace{0.2cm}0 \le q \le 1 \hspace{0.05cm}.$$ | ||
| − | + | Due to the Markov property of this source, the entropy can be determined in different ways: | |
| − | * | + | *One calculates the first two entropy approximations $H_1$ and $H_2$. Then the following applies to the actual entropy: |
| − | :$$H | + | :$$H= H_{k \to \infty} = 2 \cdot H_{\rm 2} - H_{\rm 1} \hspace{0.05cm}.$$ |
| − | * | + | *However, according to the "direct calculation method", the entropy can also be written as follows (nine terms in total): |
:$$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + \ \text{...} | :$$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + \ \text{...} | ||
\hspace{0.05cm}, \ | \hspace{0.05cm}, \ | ||
| Line 24: | Line 24: | ||
| + | ''Hint:'' | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Discrete_Sources_with_Memory|Discrete Sources with Memory]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Discrete_Sources_with_Memory#Non-binary_Markov_sources|Non-binary Markov sources]]. | ||
| + | *For all entropies, add the pseudo-unit "bit/symbol". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {For which parameters $p$ and $q$ does the maximum entropy per symbol result? |
|type="{}"} | |type="{}"} | ||
$p \ = \ $ { 0.333 1% } | $p \ = \ $ { 0.333 1% } | ||
$q\ = \ $ { 1 1% } | $q\ = \ $ { 1 1% } | ||
| − | $H_\text{max} \ = \ $ { 1.585 1% } $\ \rm bit/ | + | $H_\text{max} \ = \ $ { 1.585 1% } $\ \rm bit/symbol$ |
| − | { | + | {Let $p = 1/4$ and $q = 1$. What is the value of the first entropy approximation in this case? |
|type="{}"} | |type="{}"} | ||
| − | $H_1 = \ \ $ { 1.585 3% } $\ \rm bit/ | + | $H_1 = \ \ $ { 1.585 3% } $\ \rm bit/symbol$ |
| − | { | + | {Furthermore, let $p = 1/4$ and $q = 1$. What value results in this case for the second entropy approximation? |
|type="{}"} | |type="{}"} | ||
| − | $H_2 = \ \ $ { 1.5425 1% } $\ \rm bit/ | + | $H_2 = \ \ $ { 1.5425 1% } $\ \rm bit/symbol$ |
| − | { | + | {What is the actual source entropy $H= H_{k \to \infty}$ with $p = 1/4$ and $q = 1$? |
|type="{}"} | |type="{}"} | ||
| − | $H = \ \ $ { 1.5 1% } $\ \rm bit/ | + | $H = \ \ $ { 1.5 1% } $\ \rm bit/symbol$ |
| − | { | + | {What is the actual source entropy $H= H_{k \to \infty}$ with $p = 1/2$ and $q = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $H = \ \ $ { 0.667 1% } $\ \rm bit/ | + | $H = \ \ $ { 0.667 1% } $\ \rm bit/symbol$ |
| Line 66: | Line 66: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The maximum entropy results when the symbols $\rm A$, $\rm B$ and $\rm C$ are equally probable and the symbols within the sequence are statistically independent of each other. Then the following must apply: |
| − | [[File:Inf_Z_1_6_vers2.png|right|frame| | + | [[File:Inf_Z_1_6_vers2.png|right|frame|Transition diagram for $p = 1/4$, $q = 1$]] |
* $p_{\rm A} = p_{\rm A|A} = p_{\rm A|B} = p_{\rm A|C} = 1/3$, | * $p_{\rm A} = p_{\rm A|A} = p_{\rm A|B} = p_{\rm A|C} = 1/3$, | ||
* $p_{\rm B} = p_{\rm B|A} = p_{\rm B|B} = p_{\rm B|C} = 1/3$, | * $p_{\rm B} = p_{\rm B|A} = p_{\rm B|B} = p_{\rm B|C} = 1/3$, | ||
| Line 75: | Line 75: | ||
| − | + | From this, the values we are looking for can be determined: | |
| − | * | + | *For example, from $p_{\rm C|C} = 1/3$ one obtains the value $p \hspace{0.15cm}\underline{= 1/3}$. |
| − | * | + | *If one also takes into account the relationship $p_{\rm A|A} = p \cdot q$, then $q \hspace{0.15cm}\underline{= 1}$. |
| − | * | + | *This gives the maximum entropy $H_\text{max} ={\rm log_2} \ 3\hspace{0.15cm}\underline{= 1.585\ \rm bit/symbol}$. |
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' With the parameter values $p = 1/4$ and $q = 1$ , we obtain the adjacent transition diagram, which has the following symmetries: | ||
| + | * $p_{\rm A|A} = p_{\rm B|B} = p_{\rm C|C} = 1/4$ (marked in red), | ||
| + | * $p_{\rm A|B} = p_{\rm B|C} = p_{\rm C|A} = 1/2$ (marked in green), | ||
| + | *$p_{\rm A|C} = p_{\rm B|A} = p_{\rm C|CB} = 1/4$ (marked in blue). | ||
| + | |||
| + | |||
| + | It is obvious that the symbol probabilities are all equal: | ||
| − | |||
:$$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/3 \hspace{0.3cm} | :$$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/3 \hspace{0.3cm} | ||
| − | \Rightarrow \hspace{0.3cm} H_1 = {\rm log_2}\hspace{0.1cm} 3 \hspace{0.15cm} \underline {= 1.585 \,{\rm bit/ | + | \Rightarrow \hspace{0.3cm} H_1 = {\rm log_2}\hspace{0.1cm} 3 \hspace{0.15cm} \underline {= 1.585 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| + | '''(3)''' For the second entropy approximation one needs $3^2 = 9$ joint probabilities. | ||
| + | *Using the result from '''(2)''' , one obtains for this: | ||
:$$p_{\rm AA} = p_{\rm BB}= p_{\rm CC}= p_{\rm AC}=p_{\rm BA}=p_{\rm CB}=1/12 \hspace{0.05cm},\hspace{0.5cm} | :$$p_{\rm AA} = p_{\rm BB}= p_{\rm CC}= p_{\rm AC}=p_{\rm BA}=p_{\rm CB}=1/12 \hspace{0.05cm},\hspace{0.5cm} | ||
p_{\rm AB} = p_{\rm BC}=p_{\rm CA}=1/6$$ | p_{\rm AB} = p_{\rm BC}=p_{\rm CA}=1/6$$ | ||
| − | :$$\Rightarrow \hspace{0.2cm} H_2 = \frac{1}{2} \cdot \left [ 6 \cdot \frac{1}{12} \cdot {\rm | + | :$$\Rightarrow \hspace{0.2cm} H_2 = \frac{1}{2} \cdot \left [ 6 \cdot \frac{1}{12} \cdot {\rm log_2}\hspace{0.1cm} 12 + |
3 \cdot \frac{1}{6} \cdot {\rm log_2}\hspace{0.1cm} 6 \right ] = \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 4 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 3 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 2 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 3 | 3 \cdot \frac{1}{6} \cdot {\rm log_2}\hspace{0.1cm} 6 \right ] = \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 4 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 3 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 2 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 3 | ||
| − | = \frac{3}{4} + \frac{{\rm log_2}\hspace{0.1cm} 3}{2} \hspace{0.15cm} \underline {= 1.5425 \,{\rm bit/ | + | = \frac{3}{4} + \frac{{\rm log_2}\hspace{0.1cm} 3}{2} \hspace{0.15cm} \underline {= 1.5425 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| − | :$$H = 2 \cdot H_2 - H_1 = \big [ {3}/{2} + {\rm log_2}\hspace{0.1cm} 3 \big ] - {\rm log_2}\hspace{0.1cm} 3\hspace{0.15cm} \underline {= 1.5 \,{\rm bit/ | + | '''(4)''' Due to the Markov property of the source, the following holds true: |
| + | :$$H = H_{k \to \infty}= 2 \cdot H_2 - H_1 = \big [ {3}/{2} + {\rm log_2}\hspace{0.1cm} 3 \big ] - {\rm log_2}\hspace{0.1cm} 3\hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *One would arrive at the same result according to the following calculation: | |
:$$H= p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + ... \hspace{0.1cm}= 6 \cdot \frac{1}{12} \cdot {\rm log_2}\hspace{0.1cm} 4 + 3 \cdot \frac{1}{16} \cdot {\rm log_2}\hspace{0.1cm} 2 | :$$H= p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + ... \hspace{0.1cm}= 6 \cdot \frac{1}{12} \cdot {\rm log_2}\hspace{0.1cm} 4 + 3 \cdot \frac{1}{16} \cdot {\rm log_2}\hspace{0.1cm} 2 | ||
| − | \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/ | + | \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | [[File:Inf_Z_1_6e_vers2.png|right|frame| | + | |
| − | '''(5)''' | + | [[File:Inf_Z_1_6e_vers2.png|right|frame|Transition diagram for $p = 1/4$, $q = 0$]] |
| − | * | + | '''(5)''' From the adjacent transition diagram with the current parameters, one can see that in the case of stationarity $p_{\rm B} = 0$ will apply, since $\rm B$ can occur at most once at the starting time. |
| − | * | + | *So there is a binary Markov chain with the symbols $\rm A$ and $\rm C$ . |
| + | *The symbol probabilities are therefore given by: | ||
:$$p_{\rm A} = 0.5 \cdot p_{\rm C} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm A} + p_{\rm C} = 1 \hspace{0.3cm} | :$$p_{\rm A} = 0.5 \cdot p_{\rm C} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm A} + p_{\rm C} = 1 \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} p_{\rm A} = 1/3 \hspace{0.05cm}, \hspace{0.2cm} p_{\rm C} = 2/3\hspace{0.05cm}. $$ | \Rightarrow \hspace{0.3cm} p_{\rm A} = 1/3 \hspace{0.05cm}, \hspace{0.2cm} p_{\rm C} = 2/3\hspace{0.05cm}. $$ | ||
| − | * | + | *This gives the following probabilities: |
:$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm}0\hspace{0.7cm} \Rightarrow \hspace{0.3cm} p_{\rm AA} = 0 \hspace{0.05cm},$$ | :$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm}0\hspace{0.7cm} \Rightarrow \hspace{0.3cm} p_{\rm AA} = 0 \hspace{0.05cm},$$ | ||
:$$ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}C} =1/2\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm CA} = | :$$ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}C} =1/2\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm CA} = | ||
| Line 128: | Line 134: | ||
p_{\rm CC} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}C}}= | p_{\rm CC} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}C}}= | ||
0 + 1/3 \cdot 1 + 1/3 \cdot 0 + 1/3 \cdot 1 | 0 + 1/3 \cdot 1 + 1/3 \cdot 0 + 1/3 \cdot 1 | ||
| − | \hspace{0.15cm} \underline {= 0.667 \,{\rm bit/ | + | \hspace{0.15cm} \underline {= 0.667 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 134: | Line 140: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.2 Sources with Memory^]] |
Latest revision as of 13:05, 10 August 2021
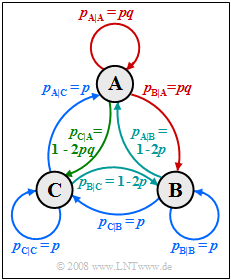
The diagram on the right shows a Markov source with $M = 3$ states $\rm A$, $\rm B$ and $\rm C$.
Let the two parameters of this Markov process be:
- $$0 \le p \le 0.5 \hspace{0.05cm},\hspace{0.2cm}0 \le q \le 1 \hspace{0.05cm}.$$
Due to the Markov property of this source, the entropy can be determined in different ways:
- One calculates the first two entropy approximations $H_1$ and $H_2$. Then the following applies to the actual entropy:
- $$H= H_{k \to \infty} = 2 \cdot H_{\rm 2} - H_{\rm 1} \hspace{0.05cm}.$$
- However, according to the "direct calculation method", the entropy can also be written as follows (nine terms in total):
- $$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + \ \text{...} \hspace{0.05cm}, \ \text{wobei} \ p_{\rm AA} = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.05cm},\hspace{0.2cm} p_{\rm AB} = p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.05cm}, \ \text{...}$$
Hint:
- The exercise belongs to the chapter Discrete Sources with Memory.
- Reference is made in particular to the page Non-binary Markov sources.
- For all entropies, add the pseudo-unit "bit/symbol".
Questions
Solution
- $p_{\rm A} = p_{\rm A|A} = p_{\rm A|B} = p_{\rm A|C} = 1/3$,
- $p_{\rm B} = p_{\rm B|A} = p_{\rm B|B} = p_{\rm B|C} = 1/3$,
- $p_{\rm C} = p_{\rm C|A} = p_{\rm C|B} = p_{\rm C|C} = 1/3$.
From this, the values we are looking for can be determined:
- For example, from $p_{\rm C|C} = 1/3$ one obtains the value $p \hspace{0.15cm}\underline{= 1/3}$.
- If one also takes into account the relationship $p_{\rm A|A} = p \cdot q$, then $q \hspace{0.15cm}\underline{= 1}$.
- This gives the maximum entropy $H_\text{max} ={\rm log_2} \ 3\hspace{0.15cm}\underline{= 1.585\ \rm bit/symbol}$.
(2) With the parameter values $p = 1/4$ and $q = 1$ , we obtain the adjacent transition diagram, which has the following symmetries:
- $p_{\rm A|A} = p_{\rm B|B} = p_{\rm C|C} = 1/4$ (marked in red),
- $p_{\rm A|B} = p_{\rm B|C} = p_{\rm C|A} = 1/2$ (marked in green),
- $p_{\rm A|C} = p_{\rm B|A} = p_{\rm C|CB} = 1/4$ (marked in blue).
It is obvious that the symbol probabilities are all equal:
- $$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/3 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_1 = {\rm log_2}\hspace{0.1cm} 3 \hspace{0.15cm} \underline {= 1.585 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(3) For the second entropy approximation one needs $3^2 = 9$ joint probabilities.
- Using the result from (2) , one obtains for this:
- $$p_{\rm AA} = p_{\rm BB}= p_{\rm CC}= p_{\rm AC}=p_{\rm BA}=p_{\rm CB}=1/12 \hspace{0.05cm},\hspace{0.5cm} p_{\rm AB} = p_{\rm BC}=p_{\rm CA}=1/6$$
- $$\Rightarrow \hspace{0.2cm} H_2 = \frac{1}{2} \cdot \left [ 6 \cdot \frac{1}{12} \cdot {\rm log_2}\hspace{0.1cm} 12 + 3 \cdot \frac{1}{6} \cdot {\rm log_2}\hspace{0.1cm} 6 \right ] = \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 4 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 3 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 2 + \frac{1}{4} \cdot {\rm log_2}\hspace{0.1cm} 3 = \frac{3}{4} + \frac{{\rm log_2}\hspace{0.1cm} 3}{2} \hspace{0.15cm} \underline {= 1.5425 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(4) Due to the Markov property of the source, the following holds true:
- $$H = H_{k \to \infty}= 2 \cdot H_2 - H_1 = \big [ {3}/{2} + {\rm log_2}\hspace{0.1cm} 3 \big ] - {\rm log_2}\hspace{0.1cm} 3\hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
- One would arrive at the same result according to the following calculation:
- $$H= p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + ... \hspace{0.1cm}= 6 \cdot \frac{1}{12} \cdot {\rm log_2}\hspace{0.1cm} 4 + 3 \cdot \frac{1}{16} \cdot {\rm log_2}\hspace{0.1cm} 2 \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
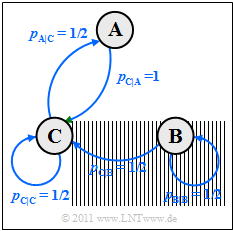
(5) From the adjacent transition diagram with the current parameters, one can see that in the case of stationarity $p_{\rm B} = 0$ will apply, since $\rm B$ can occur at most once at the starting time.
- So there is a binary Markov chain with the symbols $\rm A$ and $\rm C$ .
- The symbol probabilities are therefore given by:
- $$p_{\rm A} = 0.5 \cdot p_{\rm C} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm A} + p_{\rm C} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm A} = 1/3 \hspace{0.05cm}, \hspace{0.2cm} p_{\rm C} = 2/3\hspace{0.05cm}. $$
- This gives the following probabilities:
- $$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm}0\hspace{0.7cm} \Rightarrow \hspace{0.3cm} p_{\rm AA} = 0 \hspace{0.05cm},$$
- $$ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}C} =1/2\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm CA} = p_{\rm C} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}C} = 2/3 \cdot 1/2 = 1/3 \hspace{0.05cm},\hspace{0.2cm}{\rm log_2}\hspace{0.1cm}(1/p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}C} )= 1\hspace{0.05cm},$$
- $$ p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}A} =1\hspace{0.7cm} \Rightarrow \hspace{0.3cm} p_{\rm AC} = p_{\rm A} \cdot p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}A} = 1/3 \cdot 1 = 1/3 \hspace{0.05cm},\hspace{0.61cm}{\rm log_2}\hspace{0.1cm}(1/p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}A} )= 0\hspace{0.05cm},$$
- $$ p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}C} =1/2\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm CC} = p_{\rm C} \cdot p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}C} = 2/3 \cdot 1/2 = 1/3\hspace{0.05cm},\hspace{0.2cm}{\rm log_2}\hspace{0.1cm}(1/p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}C} )= 1 $$
- $$\Rightarrow \hspace{0.25cm} H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} +p_{\rm CA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}C}}+ p_{\rm AC} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm CC} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm C\hspace{0.01cm}|\hspace{0.01cm}C}}= 0 + 1/3 \cdot 1 + 1/3 \cdot 0 + 1/3 \cdot 1 \hspace{0.15cm} \underline {= 0.667 \,{\rm bit/symbol}} \hspace{0.05cm}.$$