Difference between revisions of "Aufgaben:Exercise 2.1Z: DSB-AM without/with Carrier"
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Double-Sideband_Amplitude_Modulation |
}} | }} | ||
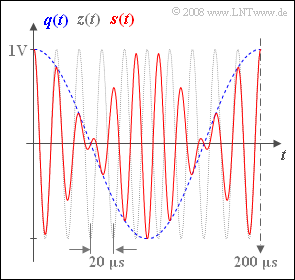
| − | [[File:P_ID987__Mod_Z_2_1.png|right|frame| | + | [[File:P_ID987__Mod_Z_2_1.png|right|frame|The signals involved in this AM]] |
| − | + | The red curve on the graph shows a section of the transmitted signal $s(t) = q(t) · z(t)$ of a double-sideband amplitude modulation (abbreviated as DSB-AM) without carrier. The duration of the time interval is $\rm 200 \ µ s$. | |
| − | + | Additionally plotted in the graph are: | |
| − | * | + | *the source signal (as a blue dashed curve): |
:$$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$ | :$$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$ | ||
| − | * | + | *the carrier signal (as a grey dashed trace): |
| − | :$$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ | + | :$$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}).$$ |
| − | + | From subtask '''(4)''' onwards, the "DSB-AM with carrier" is considered. In that case, with $A_{\rm T} = 2\text{ V}$: | |
:$$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$ | :$$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$ | ||
| Line 19: | Line 19: | ||
| − | + | Hints: | |
| − | + | *This exercise belongs to the chapter [[Modulation_Methods/Double-Sideband_Amplitude_Modulation|Double-Sideband Amplitude Modulation]]. | |
| − | + | *Particlar reference is made to the pages [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Description_in_the_time_domain|Description in the time domain]] and [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Double-Sideband_Amplitude_Modulation_with_carrier|Double-Sideband Amplitude Modulation with carrier]]. | |
| − | |||
| − | * | ||
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {From the graph, determine the phase values of the message and carrier signals. |
|type="{}"} | |type="{}"} | ||
| − | $\phi_{\rm N} \ = \ $ { 0. } $\ \text{ | + | $\phi_{\rm N} \ = \ $ { 0. } $\ \text{degrees}$ |
| − | $\phi_{\rm T} \ = \ $ { 0. } $\ \text{ | + | $\phi_{\rm T} \ = \ $ { 0. } $\ \text{degrees}$ |
| − | { | + | {What is the frequency $f_{\rm N}$ of the message signal $q(t)$ and what is the frequency $f_{\rm T}$ of the carrier signal $z(t)$? |
|type="{}"} | |type="{}"} | ||
$f_{\rm N} \ = \ $ { 5 3% } $\ \text{kHz}$ | $f_{\rm N} \ = \ $ { 5 3% } $\ \text{kHz}$ | ||
$f_{\rm T} \ = \ $ { 50 3% } $\ \text{kHz}$ | $f_{\rm T} \ = \ $ { 50 3% } $\ \text{kHz}$ | ||
| − | { | + | {Analyze the zero crossings of $s(t)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + All zero crossings of $z(t)$ are preserved in $s(t)$. |
| − | + | + | + There are additional zero crossings caused by $q(t)$. |
| − | - | + | - $s(t) = a(t) · \cos(ω_T · t)$ holds with $a(t) = |q(t)|$. |
| − | { | + | {Determine the spectral function $S(f)$ by convolution. Which (positive) frequencies $f_1$ and $f_2 > f_1$ are included in the signal?? |
|type="{}"} | |type="{}"} | ||
$f_1 \ = \ $ { 45 3% } $\ \text{kHz}$ | $f_1 \ = \ $ { 45 3% } $\ \text{kHz}$ | ||
$f_2\ = \ $ { 55 3% } $\ \text{kHz}$ | $f_2\ = \ $ { 55 3% } $\ \text{kHz}$ | ||
| − | { | + | {Let $A_{\rm T} = 2\text{ V}$. What is the modulation depth $m$? |
|type="{}"} | |type="{}"} | ||
$m \ = \ $ { 0.5 3% } | $m \ = \ $ { 0.5 3% } | ||
| − | { | + | {Which of the statements are true for "DSB–AM with carrier" and $A_{\rm T} = 2\text{ V}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + $S(f)$ | + | + $S(f)$ now includes Dirac delta functions at $±f_{\rm T}$. |
| − | - | + | - The weights of these Dirac delta lines are each $2\text{ V}$. |
| − | + $q(t)$ | + | + $q(t)$ can be seen in the envelope of $s(t)$. |
| − | - | + | - Due to the additional carrier component, the power remains unchanged. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Both signals are cosine ⇒ $ϕ_{\rm N} \hspace{0.15cm}\underline { = 0}$ and $ϕ_{\rm T} \hspace{0.15cm}\underline { = 0}$. |
| + | |||
| + | |||
| + | '''(2)''' From the graph, the period durations of $200$ μs and $20$ μs can be seen for $q(t)$ and $z(t)$, respectively. | ||
| + | *This gives the frequencies as $f_{\rm N} \hspace{0.15cm}\underline { = 5}$ kHz and $f_{\rm T} \hspace{0.15cm}\underline { = 50}$ kHz. | ||
| − | |||
| − | |||
| + | '''(3)''' <u>Answers 1 and 2</u> are correct: | ||
| + | *The zero crossings of $z(t)$ at $±5$ μs, $±15$ μs, $±25$ μs, ... ... are also present in the signal $s(t)$ ⇒ Answer 1 is correct. | ||
| + | *Other zero intersects of $s(t)$ – cause by $q(t)$ – are present at $±50$ μs, $±150$ μs, $±250$ μs, .... ⇒ Answer 2 is also correct. | ||
| + | *In contrast, the third statement is not true. Instead, $ s(t) = a(t) \cdot \cos[\omega_{\rm T} t + \phi (t)] \hspace{0.05cm}.$ | ||
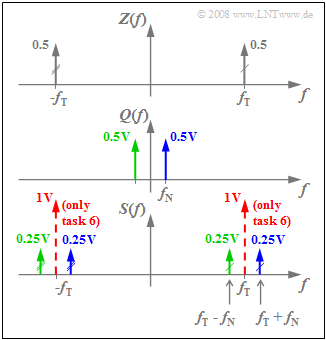
| + | [[File:EN_Mod_Z_2_1_d.png|right|frame|DSB–AM spectra $Z(f)$, $Q(f)$ and $S(f)$]] | ||
| − | + | *For $q(t) > 0$ the phase function is $ϕ(t) = 0$ and $s(t)$ coincides with $z(t)$. | |
| − | * | + | *In contrast, for $q(t) < 0$: $ϕ(t) = π = 180^\circ$. |
| − | + | *At the zero crossings of $q(t)$, the modulated signal $s(t)$ exhibits phase jumps. | |
| − | |||
| − | |||
| − | * | ||
| − | * | ||
| − | + | '''(4)''' The spectrum $S(f)$ results from the convolution of the spectral functions $Z(f)$ and $Q(f)$, each consisting of only two Dirac delta functions. The graph displays the result. | |
| − | '''(4)''' | + | *The Dirac delta functions plotted in red apply only to the "DSB-AM with carrier" and refer to subtask ('''6)'''. |
| − | * | + | *Convolution of the two $Z(f)$ Dirac delta functions at $f_{\rm T} = 50\text{ kHz}$ with $Q(f)$ leads to the Dirac delta lines at $f_{\rm T} - f_{\rm N}$ and $f_{\rm T} + f_{\rm N}$, each with weight $0.5 · 0.5\text{ V}= 0.25\text{ V}$. |
| − | * | + | *Thus, the desired values are $f_1\hspace{0.15cm}\underline { = 45 \ \rm kHz}$ and $f_1\hspace{0.15cm}\underline { = 55 \ \rm kHz}$. |
| − | * | + | *The Dirac function $0.5 · δ(f + f_{\rm T})$ with two markers leads to two more Dirac delta lines at $-f_1$ and $-f_2$. |
| − | * | ||
| − | '''(5)''' | + | '''(5)''' The modulation depth is calculated as: |
:$$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | :$$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | '''(6)''' <u>Answers 1 and 3</u> are correct: |
| − | * | + | *According to the sketch, Dirac delta lines result at $±f_{\rm T}$, both with impulse weight $A_{\rm T}/2 = 1\text{ V}$. |
| − | * | + | *At $m ≤ 1$, $q(t)$ is detectable in the envelope ⇒ envelope demodulation is applicable. |
| − | * | + | *However, this simpler receiver variant must be accounted for with a much larger transmission power. |
| − | *In | + | *In this example $(m = 0.5)$ the addition of a carrier multiplies the transmission power by nine. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 109: | Line 108: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^2.1 Double Sideband Amplitude Modulation^]] |
Latest revision as of 15:17, 18 January 2023
The red curve on the graph shows a section of the transmitted signal $s(t) = q(t) · z(t)$ of a double-sideband amplitude modulation (abbreviated as DSB-AM) without carrier. The duration of the time interval is $\rm 200 \ µ s$.
Additionally plotted in the graph are:
- the source signal (as a blue dashed curve):
- $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$
- the carrier signal (as a grey dashed trace):
- $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}).$$
From subtask (4) onwards, the "DSB-AM with carrier" is considered. In that case, with $A_{\rm T} = 2\text{ V}$:
- $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Double-Sideband Amplitude Modulation.
- Particlar reference is made to the pages Description in the time domain and Double-Sideband Amplitude Modulation with carrier.
Questions
Solution
(2) From the graph, the period durations of $200$ μs and $20$ μs can be seen for $q(t)$ and $z(t)$, respectively.
- This gives the frequencies as $f_{\rm N} \hspace{0.15cm}\underline { = 5}$ kHz and $f_{\rm T} \hspace{0.15cm}\underline { = 50}$ kHz.
(3) Answers 1 and 2 are correct:
- The zero crossings of $z(t)$ at $±5$ μs, $±15$ μs, $±25$ μs, ... ... are also present in the signal $s(t)$ ⇒ Answer 1 is correct.
- Other zero intersects of $s(t)$ – cause by $q(t)$ – are present at $±50$ μs, $±150$ μs, $±250$ μs, .... ⇒ Answer 2 is also correct.
- In contrast, the third statement is not true. Instead, $ s(t) = a(t) \cdot \cos[\omega_{\rm T} t + \phi (t)] \hspace{0.05cm}.$
- For $q(t) > 0$ the phase function is $ϕ(t) = 0$ and $s(t)$ coincides with $z(t)$.
- In contrast, for $q(t) < 0$: $ϕ(t) = π = 180^\circ$.
- At the zero crossings of $q(t)$, the modulated signal $s(t)$ exhibits phase jumps.
(4) The spectrum $S(f)$ results from the convolution of the spectral functions $Z(f)$ and $Q(f)$, each consisting of only two Dirac delta functions. The graph displays the result.
- The Dirac delta functions plotted in red apply only to the "DSB-AM with carrier" and refer to subtask (6).
- Convolution of the two $Z(f)$ Dirac delta functions at $f_{\rm T} = 50\text{ kHz}$ with $Q(f)$ leads to the Dirac delta lines at $f_{\rm T} - f_{\rm N}$ and $f_{\rm T} + f_{\rm N}$, each with weight $0.5 · 0.5\text{ V}= 0.25\text{ V}$.
- Thus, the desired values are $f_1\hspace{0.15cm}\underline { = 45 \ \rm kHz}$ and $f_1\hspace{0.15cm}\underline { = 55 \ \rm kHz}$.
- The Dirac function $0.5 · δ(f + f_{\rm T})$ with two markers leads to two more Dirac delta lines at $-f_1$ and $-f_2$.
(5) The modulation depth is calculated as:
- $$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
(6) Answers 1 and 3 are correct:
- According to the sketch, Dirac delta lines result at $±f_{\rm T}$, both with impulse weight $A_{\rm T}/2 = 1\text{ V}$.
- At $m ≤ 1$, $q(t)$ is detectable in the envelope ⇒ envelope demodulation is applicable.
- However, this simpler receiver variant must be accounted for with a much larger transmission power.
- In this example $(m = 0.5)$ the addition of a carrier multiplies the transmission power by nine.