Difference between revisions of "Aufgaben:Exercise 2.4: 2D Transfer Function"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Mobile Kommunikation/Mehrwegeempfang beim Mobilfunk}} Datei:P_ID2161__Mob_A_2_4.png|right|frame|2D–Impulsantwort $|h(\tau,…“) |
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
||
| (16 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Multipath_Reception_in_Mobile_Communications}} |
| − | [[File:P_ID2161__Mob_A_2_4.png|right|frame| | + | [[File:P_ID2161__Mob_A_2_4.png|right|frame|2D impulse response $|h(\tau, \hspace{0.05cm}t)|$]] |
| − | + | The graph shows the two-dimensional impulse response $h(\tau, \hspace{0.05cm}t)$ of a mobile radio system in magnitude representation. | |
| − | * | + | *It can be seen that the 2D impulse response only has components at delays $\tau = 0$ and $\tau = 1 \ \rm µ s$ . |
| − | * | + | *At these times: |
:$$h(\tau = 0\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$ | :$$h(\tau = 0\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$ | ||
:$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$ | :$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$ | ||
| − | + | For all other values of $\tau$, we have $h(\tau, \hspace{0.05cm}t) \equiv 0$. | |
| − | + | We want to obtain the two-dimensional transfer function $H(f, \hspace{0.05cm} t)$ as the Fourier transform of $h(\tau, t)$ with respect to the delay $\tau$: | |
:$$H(f,\hspace{0.05cm} t) | :$$H(f,\hspace{0.05cm} t) | ||
\hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | ||
| Line 19: | Line 19: | ||
| − | + | ''Notes:'' | |
| − | + | * This task belongs to chapter [[Mobile_Communications/Multi-Path_Reception_in_Mobile_Communications| Multi–Path Reception in Mobile Communications]]. | |
| − | '' | + | * A similar problem is treated in [[Aufgaben:Exercise_2.5:_Scatter_Function| Exercize 2.5]] but with a different nomenclature. |
| − | * | ||
| − | * | ||
| Line 29: | Line 27: | ||
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the period $T_0$ of the function $h(\tau = 1 \ {\rm µ s},\hspace{0.05cm} t)$? Note that the graph shows the <u>magnitude</u> $|h(\tau, \hspace{0.05cm}t)|$ . |
|type="{}"} | |type="{}"} | ||
| − | $T_0 \ = \ ${ 20 3% } $\ \rm ms$ | + | $T_0 \ = \ ${ 20 3% } $\ \ \rm ms$ |
| − | { | + | {At what times $t_1$ $($between $0$ and $10 \ \rm ms)$ and $t_2$ $($between $10 \ \ \rm ms$ and $20 \ \ \rm ms)$ is $H(f, \hspace{0.05cm}t)$ constant in $f$ ? |
|type="{}"} | |type="{}"} | ||
| − | $t_1 \ = \ ${ 5 3% } $\ \rm ms$ | + | $t_1 \ = \ ${ 5 3% } $\ \ \rm ms$ |
| − | $t_2 \ = \ ${ 15 3% } $\ \rm ms$ | + | $t_2 \ = \ ${ 15 3% } $\ \ \rm ms$ |
| − | { | + | {Calculate $H_0(f) = H(f, \hspace{0.05cm}t = 0)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + We have $H_0(f) = H_0(f + i \cdot 1 \ {\rm MHz}), \ i = ±1, ±2, \ \ \text{...}$ |
| − | + | + | + We have approximately $0.293 ≤ |H_0(f)| ≤ 1.707$. |
| − | + $|H_0(f)|$ | + | + $|H_0(f)|$ has a maximum at $f = 0$ . |
| − | { | + | {Calculate $H_{10}(f) = H(f, \hspace{0.05cm}t = 10 \ \rm ms)$. Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + We have $H_{10}(f) = H_{10}(f + i \cdot 1 \ {\rm MHz}),\ i = ±1, ±2, \ \ \text{...}$ |
| − | + | + | + We have approximately $0.293 ≤ H_{10}(f) ≤ 1.707$. |
| − | - $|H_{10}(f)|$ | + | - $|H_{10}(f)|$ has a maximum at $f = 0$ . |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The period can be read from the given graph. If the magnitude representation is taken into account, the result is $T_0 \ \underline {= 20 \ \ \rm ms}$. |
| − | '''(2)''' | + | '''(2)''' At time $t_1 \ \underline {= 5 \ \ \rm ms}$ we have $h(\tau = 1 \ {\rm µ s}, t_1) = 0$. Accordingly, the following applies |
:$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
H(f,\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} = {\rm const.}$$ | H(f,\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} = {\rm const.}$$ | ||
| − | + | The same applies to $t_2 \ \underline {= 15 \ \ \rm ms}$: | |
:$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
H(f,\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} = {\rm const.}$$ | H(f,\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} = {\rm const.}$$ | ||
| Line 68: | Line 66: | ||
| − | '''(3)''' | + | '''(3)''' At time $t = 0$ the impulse response with $\tau_1 = 1 \ \ \rm µ s$ is |
:$$h(\tau,\hspace{0.05cm}t = 0) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)+ \delta(\tau - \tau_1)\hspace{0.05cm}.$$ | :$$h(\tau,\hspace{0.05cm}t = 0) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)+ \delta(\tau - \tau_1)\hspace{0.05cm}.$$ | ||
| − | + | Its Fourier transform is | |
:$$H_0(f) = H(f,\hspace{0.05cm}t = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} + 1 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_1}=\frac{1}{ \sqrt{2}} + \cos( 2 \pi f \tau_1)- {\rm j}\cdot \sin( 2 \pi f \tau_1)$$ | :$$H_0(f) = H(f,\hspace{0.05cm}t = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} + 1 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_1}=\frac{1}{ \sqrt{2}} + \cos( 2 \pi f \tau_1)- {\rm j}\cdot \sin( 2 \pi f \tau_1)$$ | ||
:$$\Rightarrow \hspace{0.3cm} |H_0(f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | :$$\Rightarrow \hspace{0.3cm} |H_0(f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | ||
| Line 77: | Line 75: | ||
\sqrt { 0.5 + 1 + {2}/{ \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)} = \sqrt { 1.5 + { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$ | \sqrt { 0.5 + 1 + {2}/{ \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)} = \sqrt { 1.5 + { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$ | ||
| − | + | Therefore, | |
| − | * $H_0(f)$ | + | * $H_0(f)$ is periodic with $1/\tau_1 = 1 \ \rm MHz$. |
| − | * | + | * For the maximum and minimum values, we have |
:$${\rm Max}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 + { \sqrt{2}} } \approx 1.707 \hspace{0.05cm},\hspace{0.5cm}{\rm Min}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 - { \sqrt{2}} } \approx 0.293 \hspace{0.05cm}. $$ | :$${\rm Max}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 + { \sqrt{2}} } \approx 1.707 \hspace{0.05cm},\hspace{0.5cm}{\rm Min}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 - { \sqrt{2}} } \approx 0.293 \hspace{0.05cm}. $$ | ||
| − | * | + | * At $f = 0$, $|H_0(f)|$ has a maximum. |
| − | |||
| − | |||
| + | Therefore, <u>all three solution suggestions</u> are correct. | ||
| − | '''(4)''' | + | '''(4)''' For the time $t = 10 \ \rm ms$ the following equations apply: |
:$$h(\tau,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} \cdot \delta(\tau)- \delta(\tau - \tau_1)\hspace{0.05cm},$$ | :$$h(\tau,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} \cdot \delta(\tau)- \delta(\tau - \tau_1)\hspace{0.05cm},$$ | ||
:$$H_{10}(f) = H(f,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | :$$H_{10}(f) = H(f,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | ||
| Line 94: | Line 91: | ||
\sqrt { 1.5 - { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$ | \sqrt { 1.5 - { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$ | ||
| − | [[File:P_ID2163__Mob_A_2_4d.png|right|frame| | + | [[File:P_ID2163__Mob_A_2_4d.png|right|frame|2D impulse response $|h(\tau, \hspace{0.05cm}t)|$ and 2D transfer function $|H(f, \hspace{0.05cm}t)|$]] |
| − | + | <u>Solutions 1 and 2</u> are correct: | |
| − | * | + | *The frequency period does not change compaired to $t = 0$. |
| − | * | + | *The maximum value is still $1.707$ and the minimum value $0.293$ does not change compared to the subtask '''(3)'''. |
| − | * | + | *For $f = 0$ there is now a minimum and not a maximum. |
| − | + | The graph on the right shows the magnitude $|H(f, t)|$ of the 2D transfer function. | |
| Line 108: | Line 105: | ||
| − | + | [[Category:Mobile Communications: Exercises|^2.2 Multi-Path Reception in Wireless Systems^]] | |
| − | [[Category: | ||
Latest revision as of 13:38, 23 March 2021
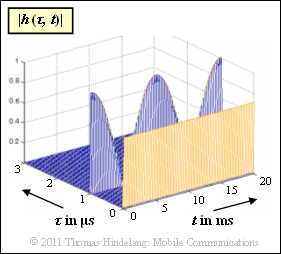
The graph shows the two-dimensional impulse response $h(\tau, \hspace{0.05cm}t)$ of a mobile radio system in magnitude representation.
- It can be seen that the 2D impulse response only has components at delays $\tau = 0$ and $\tau = 1 \ \rm µ s$ .
- At these times:
- $$h(\tau = 0\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$
- $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$
For all other values of $\tau$, we have $h(\tau, \hspace{0.05cm}t) \equiv 0$.
We want to obtain the two-dimensional transfer function $H(f, \hspace{0.05cm} t)$ as the Fourier transform of $h(\tau, t)$ with respect to the delay $\tau$:
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$
Notes:
- This task belongs to chapter Multi–Path Reception in Mobile Communications.
- A similar problem is treated in Exercize 2.5 but with a different nomenclature.
Questionnaire
Solution
(2) At time $t_1 \ \underline {= 5 \ \ \rm ms}$ we have $h(\tau = 1 \ {\rm µ s}, t_1) = 0$. Accordingly, the following applies
- $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} H(f,\hspace{0.05cm}t_1) = \frac{1}{ \sqrt{2}} = {\rm const.}$$
The same applies to $t_2 \ \underline {= 15 \ \ \rm ms}$:
- $$h(\tau = 1\,{\rm µ s},\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} H(f,\hspace{0.05cm}t_2) = \frac{1}{ \sqrt{2}} = {\rm const.}$$
(3) At time $t = 0$ the impulse response with $\tau_1 = 1 \ \ \rm µ s$ is
- $$h(\tau,\hspace{0.05cm}t = 0) = \frac{1}{ \sqrt{2}} \cdot \delta(\tau)+ \delta(\tau - \tau_1)\hspace{0.05cm}.$$
Its Fourier transform is
- $$H_0(f) = H(f,\hspace{0.05cm}t = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} + 1 \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau_1}=\frac{1}{ \sqrt{2}} + \cos( 2 \pi f \tau_1)- {\rm j}\cdot \sin( 2 \pi f \tau_1)$$
- $$\Rightarrow \hspace{0.3cm} |H_0(f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { \left [ {1}/{ \sqrt{2}} + \cos( 2 \pi f \tau_1) \right ]^2 + \left [\sin( 2 \pi f \tau_1)\right ]^2}= \sqrt { 0.5 + 1 + {2}/{ \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)} = \sqrt { 1.5 + { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$
Therefore,
- $H_0(f)$ is periodic with $1/\tau_1 = 1 \ \rm MHz$.
- For the maximum and minimum values, we have
- $${\rm Max}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 + { \sqrt{2}} } \approx 1.707 \hspace{0.05cm},\hspace{0.5cm}{\rm Min}\, \left [ \, |H_0(f)|\, \right ] \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 - { \sqrt{2}} } \approx 0.293 \hspace{0.05cm}. $$
- At $f = 0$, $|H_0(f)|$ has a maximum.
Therefore, all three solution suggestions are correct.
(4) For the time $t = 10 \ \rm ms$ the following equations apply:
- $$h(\tau,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} \cdot \delta(\tau)- \delta(\tau - \tau_1)\hspace{0.05cm},$$
- $$H_{10}(f) = H(f,\hspace{0.05cm}t = 10\,{\rm ms}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} - \cos( 2 \pi f \tau_1)+ {\rm j}\cdot \sin( 2 \pi f \tau_1)\hspace{0.05cm},$$
- $$ |H_{10}(f)| \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt { 1.5 - { \sqrt{2}} \cdot \cos( 2 \pi f \tau_1)}\hspace{0.05cm}.$$
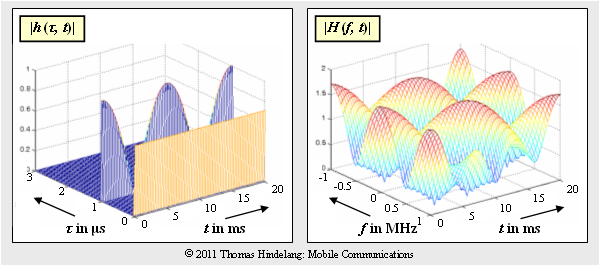
Solutions 1 and 2 are correct:
- The frequency period does not change compaired to $t = 0$.
- The maximum value is still $1.707$ and the minimum value $0.293$ does not change compared to the subtask (3).
- For $f = 0$ there is now a minimum and not a maximum.
The graph on the right shows the magnitude $|H(f, t)|$ of the 2D transfer function.