Difference between revisions of "Aufgaben:Exercise 2.1Z: 2D-Frequency and 2D-Time Representations"
From LNTwww
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
|||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/General_Description_of_Time_Variant_Systems}} |
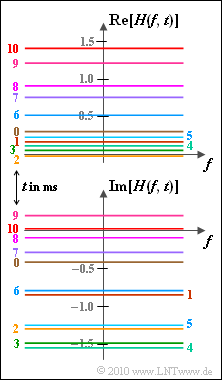
| − | [[File:P_ID2145__Mob_z_2_1.png|right|frame|2D& | + | [[File:P_ID2145__Mob_z_2_1.png|right|frame|2D transfer function: <br>real and imaginary parts]] |
| − | To describe a time-variant channel with several paths, the | + | To describe a time-variant channel with several paths, the '''two-dimensional impulse response''' is used: |
| − | $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$ | + | :$$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$ |
| − | The first parameter $(\tau)$ indicates the delay, the second $(t)$ is related to the time variance of the channel. | + | The first parameter $(\tau)$ indicates the delay, the second parameter $(t)$ is related to the time variance of the channel. |
| − | The Fourier transform of $h(\tau, t)$ | + | The Fourier transform of $h(\tau, \ t)$ with respect to $\tau$ is the '''time-variant transfer function''': |
:$$H(f,\hspace{0.05cm} t) | :$$H(f,\hspace{0.05cm} t) | ||
\hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In the graph, $H(f, t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$. | + | *In the graph, $H(f, \ t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$. |
| − | In general, $H(f, t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately. | + | *In general, $H(f, \ t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately. |
| Line 24: | Line 24: | ||
''Notes:'' | ''Notes:'' | ||
| − | * This task belongs to | + | * This task belongs to the chapter [[Mobile_Communications/General_Description_of_Time_Variant_Systems|General description of time–variant systems]]. |
| − | * In the above equation, an single-path channel is represented with | + | * In the above equation, an single-path channel is represented with parameter $M = 1$ . |
* Here are some numerical values of the specified time-variant transfer function: | * Here are some numerical values of the specified time-variant transfer function: | ||
| − | $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} | + | :$$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} |
H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$ | H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$ | ||
| − | $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} | + | :$$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} |
H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$ | H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$ | ||
| − | $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} | + | :$$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} |
H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$ | H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$ | ||
| − | * As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, t)$ are zero-mean. | + | * As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, \ t)$ are zero-mean. |
| − | ===Questionnaire== | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
{Is the channel time-variant? | {Is the channel time-variant? | ||
| Line 52: | Line 52: | ||
{How can the 2D impulse response be described here? | {How can the 2D impulse response be described here? | ||
|type="[]"} | |type="[]"} | ||
| − | - $h(\tau, t) = A \cdot \delta(\tau) + B \cdot \delta(\tau \, –5 \, \rm µ s)$. | + | - $h(\tau, \ t) = A \cdot \delta(\tau) + B \cdot \delta(\tau \, –5 \, \rm µ s)$. |
| − | - $h(\tau, t) = A \cdot \delta(\tau)$. | + | - $h(\tau, \ t) = A \cdot \delta(\tau)$. |
| − | + $h(\tau, t) = z(t) \cdot \delta(\tau)$. | + | + $h(\tau, \ t) = z(t) \cdot \delta(\tau)$. |
| − | {Estimate | + | {Estimate for which channel the data was recorded. |
|type="()"} | |type="()"} | ||
- AWGN channel, | - AWGN channel, | ||
| Line 64: | Line 64: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
| − | + | {{ML-Kopf}} | |
| − | '''(1)''' As can be seen in the graph, the transfer function $H(f, t)$ | + | '''(1)''' As can be seen in the graph, the transfer function $H(f, \ t)$ depends on $t$. Thus $h(\tau, \ t)$ is also time-dependent. Correct is therefore <u>YES</u>. |
| − | '''(2)''' If we look at a fixed point in time, for example $t = 2 \ \rm ms$, we obtain the following for the time-variant transfer function | + | '''(2)''' If we look at a fixed point in time, for example $t = 2 \ \rm ms$, we obtain the following for the time-variant transfer function: |
| − | $$H(f,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \hspace{0.05cm} = {\rm const.}$$ | + | :$$H(f,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \hspace{0.05cm} = {\rm const.}$$ |
| − | Thus the corresponding 2D–impulse response is | + | *Thus the corresponding 2D–impulse response is |
| − | $$h(\tau,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \cdot \delta (\tau) \hspace{0.05cm} | + | :$$h(\tau,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \cdot \delta (\tau) \hspace{0.05cm} |
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} M = 1 \hspace{0.05cm}.$$ | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} M = 1 \hspace{0.05cm}.$$ | ||
| − | + | *There is only one path $(M=1)$. This means that the correct solution is <u>NO</u>. | |
| + | |||
'''(3)''' The correct solution is <u>solution 3</u>: | '''(3)''' The correct solution is <u>solution 3</u>: | ||
*There is time variance but no frequency selectivity. | *There is time variance but no frequency selectivity. | ||
| − | * | + | *Options 1 and 2, on the other hand, describe time-invariant systems. |
| − | '''(4)''' | + | '''(4)''' <u>Solution 4</u> is correct: |
| − | *For the AWGN | + | *For the AWGN channel, no transfer function can be specified. |
| − | *For a two-way channel, $H(f, t)$ is | + | *For a two-way channel, $H(f, \ t)$ is not a constant in $f$ for any $t$. |
| − | *Since in the $H(f, t)$& | + | *Since in the $H(f, \ t)$ graph the real and imaginary part have a non-zero mean ⇒ the Rayleigh–channel can also be excluded. |
| − | *The data for the present task comes from a [[ | + | *The data for the present task comes from a [[Mobile_Communications/Non-Frequency_Selective_Fading_With_Direct_Component| Rice channel]] with following parameters: |
:$$\sigma = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} | :$$\sigma = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} | ||
x_0 = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm}y_0 = -{1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} | x_0 = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm}y_0 = -{1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} | ||
| − | f_{\rm D,\hspace{0.05cm} max} = 100\,\,{\rm Hz}\hspace{0.05cm}.$ | + | f_{\rm D,\hspace{0.05cm} max} = 100\,\,{\rm Hz}\hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^2.1 Description of Time-Variant Systems^]] |
Latest revision as of 13:37, 23 March 2021
To describe a time-variant channel with several paths, the two-dimensional impulse response is used:
- $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)\hspace{0.05cm}.$$
The first parameter $(\tau)$ indicates the delay, the second parameter $(t)$ is related to the time variance of the channel.
The Fourier transform of $h(\tau, \ t)$ with respect to $\tau$ is the time-variant transfer function:
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$
- In the graph, $H(f, \ t)$ is displayed as a function of frequency, for different values of absolute time $t$ in the range of $0 \ \text{...} \ 10 \ \rm ms$.
- In general, $H(f, \ t)$ is complex. The real part (top) and the imaginary part (bottom) are drawn separately.
Notes:
- This task belongs to the chapter General description of time–variant systems.
- In the above equation, an single-path channel is represented with parameter $M = 1$ .
- Here are some numerical values of the specified time-variant transfer function:
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\, {\rm ms}) \approx 0.3 - {\rm j} \cdot 0.4 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 2\, {\rm ms}) \approx 0.0 - {\rm j} \cdot 1.3 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\, {\rm ms}) \approx 0.1 - {\rm j} \cdot 1.5 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 6\, {\rm ms}) \approx 0.5 - {\rm j} \cdot 0.8 \hspace{0.05cm},$$
- $$H(f,\hspace{0.05cm} t \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 8\, {\rm ms}) \approx 0.9 - {\rm j} \cdot 0.1 \hspace{0.05cm},\hspace{0.2cm} H(f,\hspace{0.05cm} t = 10\, {\rm ms}) \approx 1.4 \hspace{0.05cm}.$$
- As can already be guessed from the above graph, neither the real nor the imaginary part of the 2D transfer function $H(f, \ t)$ are zero-mean.
Questionnaire
Solution
(1) As can be seen in the graph, the transfer function $H(f, \ t)$ depends on $t$. Thus $h(\tau, \ t)$ is also time-dependent. Correct is therefore YES.
(2) If we look at a fixed point in time, for example $t = 2 \ \rm ms$, we obtain the following for the time-variant transfer function:
- $$H(f,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \hspace{0.05cm} = {\rm const.}$$
- Thus the corresponding 2D–impulse response is
- $$h(\tau,\hspace{0.05cm} t = 2\, {\rm ms}) = - {\rm j} \cdot 1.3 \cdot \delta (\tau) \hspace{0.05cm} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} M = 1 \hspace{0.05cm}.$$
- There is only one path $(M=1)$. This means that the correct solution is NO.
(3) The correct solution is solution 3:
- There is time variance but no frequency selectivity.
- Options 1 and 2, on the other hand, describe time-invariant systems.
(4) Solution 4 is correct:
- For the AWGN channel, no transfer function can be specified.
- For a two-way channel, $H(f, \ t)$ is not a constant in $f$ for any $t$.
- Since in the $H(f, \ t)$ graph the real and imaginary part have a non-zero mean ⇒ the Rayleigh–channel can also be excluded.
- The data for the present task comes from a Rice channel with following parameters:
- $$\sigma = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} x_0 = {1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm}y_0 = -{1}/{\sqrt{2}} \hspace{0.05cm},\hspace{0.2cm} f_{\rm D,\hspace{0.05cm} max} = 100\,\,{\rm Hz}\hspace{0.05cm}.$$