Aufgaben:Exercise 2.2Z: Real Two-Path Channel

• Return to book

Two-path scenario

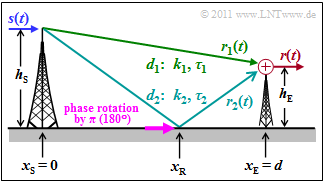
The sketched scenario is considered in which the transmitted signal  $s(t)$  reaches the antenna of the receiver via two paths:

$$r(t) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} r_1(t) + r_2(t) =k_1 \cdot s( t - \tau_1) + k_2 \cdot s( t - \tau_2) \hspace{0.05cm}.$$

Note the following:

• The delays  $\tau_1$  and  $\tau_2$  of the main and the secondary paths can be calculated from the path lengths  $d_1$  and  $d_2$  using the speed of light  $c = 3 \cdot 10^8 \ \rm m/s$ .
• The amplitude factors  $k_1$  and  $k_2$  are obtained according to the path loss model with path loss exponent  $\gamma = 2$  (free–space attenuation).
• The height of the transmit antenna is  $h_{\rm S} = 500 \ \rm m$.  The height of the receiving antenna is  $h_{\rm E} = 30 \ \rm m$.  The antennas are separated by a distance of  $d = 10 \ \ \rm km$.
• The reflection on the secondary path causes a phase change of  $\pi$, so that the partial signals must be subtracted.  This is taken into account by a negative  $k_2$ value.

Note:

• This task belongs to the chapter   Multi–Path Reception in Mobile Communications.

Questionnaire

1

Calculate the length  $d_1$  of the direct path.

$d_1 \ = \ $ $\ \ \rm m$

2

Calculate the length  $d_2$  of the reflected path.

$d_2 \ = \ $ $\ \ \rm m$

3

Which differences  $\Delta d = d_2 \ - d_1$  and  $\Delta \tau = \tau_2 -\tau_1$  (term) result from exact calculation?

$\Delta d \ = \ $ $\ \ \rm m$

$\Delta \tau \ = \ $ $\ \ \rm ns$

4

What equation results for the path delay difference  $\Delta \tau$  with the approximation $\sqrt{(1 + \varepsilon)} \approx 1 + \varepsilon/2$  valid for small  $\varepsilon$ ?

	$\Delta \tau = (h_{\rm S} \ - h_{\rm E})/d$,
	$\Delta \tau = (h_{\rm S} \ - h_{\rm E})/(c \cdot d)$,
	$\Delta \tau = 2 \cdot h_{\rm S} \cdot h_{\rm E}/(c \cdot d)$.

5

Which statements apply for the amplitude coefficients  $k_1$  and  $k_2$ ?

	The coefficients  $k_1$  and  $k_2$  are almost equal in magnitude.
	The magnitudes  $|k_1|$  and  $|k_2|$  differ significantly.
	The coefficients  $|k_1|$  and  $|k_2|$  differ in sign.

Solution

Solution

(1)  According to Pythagoras:

$$d_1 = \sqrt{d^2 + (h_{\rm S}- h_{\rm E})^2} = \sqrt{10^2 + (0.5- 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10011.039\,{\rm m}} \hspace{0.05cm}.$$

• Actually, specifying such a length with an accuracy of one millimeter is not very useful and contradicts the mentality of an engineer.
• We have done this anyway to be able to check the accuracy of the approximation in subtask  (4).

(2)  If you fold the reflected beam on the right side of  $x_{\rm R}$  downwards  (reflection on the ground), you get again a right triangle.  From this follows:

$$d_2 = \sqrt{d^2 + (h_{\rm S}+ h_{\rm E})^2} = \sqrt{10^2 + (0.5+ 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10014.035\,{\rm m}} \hspace{0.05cm}.$$

(3)  Using the results from  (1)  and  (2), the length and delay differences are:

$$\Delta d = d_2 - d_1 = \hspace{0.1cm} \underline {=2.996\,{\rm m}} \hspace{0.05cm},\hspace{1cm} \Delta \tau = \frac{\Delta d}{c} = \frac{2.996\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s}} \hspace{0.1cm} \underline {=9.987\,{\rm ns}} \hspace{0.05cm}.$$

(4)  With  $h_{\rm S} + h_{\rm E} \ll d$  the above equation can be expressed as follows:

$$d_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}- h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}- h_{\rm E})^2}{2d^2} \right ] \hspace{0.05cm},\hspace{1cm} d_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{2d^2} \right ] $$

$$\Rightarrow \hspace{0.3cm} \Delta d = d_2 - d_1 \approx \frac {1}{2d} \cdot \left [ (h_{\rm S}+ h_{\rm E})^2 - (h_{\rm S}- h_{\rm E})^2 \right ] = \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{d}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \Delta \tau = \frac{\Delta d}{c} \approx \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{c \cdot d} \hspace{0.05cm}.$$

• So the correct solution is the solution 3.  With the given numerical values, we have

$$\Delta \tau \approx \frac {2 \cdot 500\,{\rm m}\cdot 30\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s} \cdot 10000\,{\rm m}} = 10^{-8}\,{\rm s} = 10\,{\rm ns} \hspace{0.05cm}.$$

• The relative error with respect to the actual value according to the subtask  (3)  is only  $0.13\%$.
• In solutions 1 and 2, the dimensions are wrong.
• In solution 2, there would be no propagation delay if both antennas were the same height.  This is clearly not true.

(5)  The path loss exponent  $\gamma = 2$  implies that the reception power  $P_{\rm E}$  decreases quadratically with distance.

• The signal amplitude thus decreases with  $1/d$, so for some constant  $K$  we have

$$k_1 = \frac {K}{d_1} \hspace{0.05cm},\hspace{0.2cm}|k_2| = \frac {K}{d_2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {|k_2|}{k_1} = \frac {d_1}{d_2}= \frac {10011,039\,{\rm m}}{10014,035\,{\rm m}} \approx 0.99 \hspace{0.05cm}.$$

• The two path weights thus only differ in magnitude by about  $1\%$.
• In addition, the coefficients  $k_1$  and  $k_2$  have different signs   ⇒   Answers 1 and 3  are correct.