Difference between revisions of "Aufgaben:Exercise 4.4Z: Contour Lines of the "2D-PDF""
From LNTwww
m (Text replacement - "[[Stochastische_Signaltheorie/" to "[[Theory_of_Stochastic_Signals/") |
|||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables |
}} | }} | ||
| − | [[File: | + | [[File:EN Sto Z 4 4.png|right|frame|Gaussian 2D–PDF: Contour lines]] |
| − | + | Given a two-dimensional Gaussian random variable $(x, y)$ with mean $(0, 0)$ and the 2D–PDF | |
| − | :$$f_{xy}(x, y) = C\cdot{\rm e}^{-(x^{\rm 2} + y^{\rm 2} +\sqrt{\rm 2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm} y)}.$$ | + | :$$f_{xy}(x,\ y) = C\cdot{\rm e}^{-(x^{\rm 2} + y^{\rm 2} +\sqrt{\rm 2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm} y)}.$$ |
| − | + | It is further known that the standard deviations are $\sigma_x=\sigma_y=1.$ | |
| − | + | Entered in the sketch are: | |
| − | * | + | * a contour line of this PDF for $f_{xy}(x,y) =0.2$, |
| − | * | + | * the (dark blue) ellipse major axis $\rm (EA)$, and |
| − | * | + | * the (red) "correlation line" or "regression line" $\rm (RL)$. |
| Line 20: | Line 20: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables|Two-dimensional Gaussian Random Variables]]. |
| + | *More information on this topic is provided in the (German language) learning video [[Gaußsche_2D-Zufallsgrößen_(Lernvideo)|"Gaußsche 2D-Zufallsgrößen"]]: | ||
| + | ::Part 1: Gaussian random variables without statistical bindings, | ||
| + | ::Part 2: Gaussian random variables with statistical bindings. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Questions=== | |
| − | |||
| − | |||
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the correlation coefficient $\rho_{xy}$? |
|type="{}"} | |type="{}"} | ||
$\rho_{xy} \ = \ $ { -0.727--0.687 } | $\rho_{xy} \ = \ $ { -0.727--0.687 } | ||
| − | { | + | {What is the maximum PDF value $C = f_{xy}(0, 0)$? |
|type="{}"} | |type="{}"} | ||
$C \ = \ $ { 0.225 3% } | $C \ = \ $ { 0.225 3% } | ||
| − | { | + | {What is the angle $\alpha$ between ellipse major axis $\rm (EA)$ and $x$–axis? |
|type="{}"} | |type="{}"} | ||
| − | $\alpha\ = \ $ { -46--44 } $ \ \rm | + | $\alpha\ = \ $ { -46--44 } $ \ \rm degrees$ |
| − | { | + | {At what values $x_0$ and $y_0$ does the contour line $f_{xy}(x,y) = 0.2$ intersect the ellipse major axis? What is the relationship between $x_0$ and $y_0$? |
|type="{}"} | |type="{}"} | ||
$x_0/y_0 \ = \ $ { -1.03--0.97 } | $x_0/y_0 \ = \ $ { -1.03--0.97 } | ||
| − | { | + | {Which statements are true regarding the correlation line $y=K\cdot x$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The correlation line is steeper than the ellipse major axis. |
| − | + | + | + The angle ofthe correlation line with respect to the $x$–axis is about $-35^\circ$. |
| − | + | + | + The correlation line intersects all contour line where a vertical tangent can be applied to the ellipse. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Even without specifying $\sigma_x = \sigma_y = 1$ one could see that the standard deviations $\sigma_x$ and $\sigma_y$ are equal, <br>since in the exponent of $f_{xy}(x, y)$ the coefficients at $x^2$ and $y^2$ are equal. |
| − | + | *By comparing coefficients, we thus obtain: | |
| − | * | ||
:$$\frac{- 2 \rho_{xy}}{\sigma_x\cdot\sigma_y} = \sqrt{2}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | :$$\frac{- 2 \rho_{xy}}{\sigma_x\cdot\sigma_y} = \sqrt{2}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
\rho_{xy}=\frac{-1}{\sqrt{2}} \hspace{0.15cm}\underline{\approx -0.707}.$$ | \rho_{xy}=\frac{-1}{\sqrt{2}} \hspace{0.15cm}\underline{\approx -0.707}.$$ | ||
| − | '''(2)''' | + | '''(2)''' Using the numerical values calculated in point '''(1)''', we obtain: |
:$$C=\frac{\rm 1}{\rm 2\it\pi\cdot\sigma_x\cdot\sigma_y\cdot\sqrt{\rm 1 - \rho_{xy}^{\rm 2}}} | :$$C=\frac{\rm 1}{\rm 2\it\pi\cdot\sigma_x\cdot\sigma_y\cdot\sqrt{\rm 1 - \rho_{xy}^{\rm 2}}} | ||
=\frac{\rm 1}{\rm 2\pi\cdot\rm 1\cdot 1\cdot\sqrt{0.5}}=\frac{\rm 1}{\sqrt{\rm 2}\cdot \pi}\hspace{0.15cm}\underline{\approx \rm 0.225}.$$ | =\frac{\rm 1}{\rm 2\pi\cdot\rm 1\cdot 1\cdot\sqrt{0.5}}=\frac{\rm 1}{\sqrt{\rm 2}\cdot \pi}\hspace{0.15cm}\underline{\approx \rm 0.225}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The general equation is: |
| − | :$$\alpha = {\rm 1}/{\rm 2}\cdot \rm arctan \ (\rm 2 \cdot\it \rho_{xy}\cdot \frac{\sigma_x\cdot\sigma_y}{\sigma_x^{\rm 2} - \sigma_y^{\rm 2}}{\rm )} | + | :$$\alpha = {\rm 1}/{\rm 2}\cdot \rm arctan \ (\rm 2 \cdot\it \rho_{xy}\cdot \frac{\sigma_x\cdot\sigma_y}{\sigma_x^{\rm 2} - \sigma_y^{\rm 2}}{\rm ).}$$ |
| − | * | + | *Applies $\sigma_x = \sigma_y$ and $\rho_{xy} \ne 0$, then the angle is always $\alpha = \pm 45^\circ$, where the sign is equal to the sign of $\rho_{xy}$. |
| − | * | + | *In the present case $\alpha\hspace{0.15cm}\underline{ = -45^\circ}$ holds. |
| − | '''(4)''' | + | '''(4)''' For the plotted contour line holds: |
| − | :$$f_{xy}(x, y)=\frac{1}{\sqrt{2}\cdot \pi}\cdot {\rm e}^{(x^{2} + | + | :$$f_{xy}(x, y)=\frac{1}{\sqrt{2}\cdot \pi}\cdot {\rm e}^{(x^{2} + y^{2} + \sqrt{2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm}y)}=0.2\hspace{0.3cm} |
| − | \Rightarrow \hspace{0.3cm}{\rm e}^{-(x^{2} + | + | \Rightarrow \hspace{0.3cm}{\rm e}^{-(x^{2} + y^{2} + \sqrt{2}\hspace{0.05cm} \cdot \hspace{0.05cm} x \hspace{0.05cm} \cdot \hspace{0.05cm}y)} = 0.8885 |
| − | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | + | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x^{\rm 2} + y^{\rm 2} + \sqrt{\rm 2}\cdot\hspace{0.05cm} x \hspace{0.05cm} \cdot \hspace{0.05cm}y = -{\rm ln(0.8885)} \approx\rm 0.118.$$ |
| − | * | + | *The angle of the ellipse major axis is $\alpha = -45^\circ$. Therefore $y_0 = - x_0$ must hold. It further follows: |
:$$x_{\rm 0}^{\rm 2} + (-x_{\rm 0})^{\rm 2} + \sqrt{\rm 2}\cdot x_{\rm 0}(-x_{\rm 0}) = 0.118$$ | :$$x_{\rm 0}^{\rm 2} + (-x_{\rm 0})^{\rm 2} + \sqrt{\rm 2}\cdot x_{\rm 0}(-x_{\rm 0}) = 0.118$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm}(\rm 2 - \sqrt{\rm 2})\cdot \it | + | :$$\Rightarrow \hspace{0.3cm}(\rm 2 - \sqrt{\rm 2})\cdot \it x_{\rm 0}^{\rm 2} = {\rm 0.118} |
| − | \hspace{0.5cm}\ | + | \hspace{0.5cm}\rightarrow \hspace{0.5cm} x_{\rm 0}^{\rm 2} \approx \frac{\rm0.118}{\rm0.585}\approx\rm 0.202; \hspace{0.5cm} {\it x}_{\rm 0}\approx\pm\rm 0.450.$$ |
| − | * | + | *The two intersections of the plotted contour lines with the ellipse major axis are thus at $(+0.45, -0.45)$ and $(-0.45, +0.45)$. |
| − | * | + | *The quotient in both cases is $x_0/y_0 \hspace{0.15cm}\underline{ = -1}$. |
| − | '''(5)''' | + | '''(5)''' Correct are <u>the proposed solutions 2 and 3</u>: |
| − | * | + | *With $\sigma_x = \sigma_y$ and the result of the subtask '''(1)''' holds for the angle of the correlation line: |
:$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x} = \arctan (\rho_{\it xy})=\arctan(-{\rm 1}/{\sqrt{\rm 2}})\approx -\rm 35.3^{\circ}.$$ | :$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x} = \arctan (\rho_{\it xy})=\arctan(-{\rm 1}/{\sqrt{\rm 2}})\approx -\rm 35.3^{\circ}.$$ | ||
| − | * | + | *This means: The first statement is false and the second is true. |
| + | |||
| + | The following is the <u>proof of the correctness of the last statement</u>: | ||
| + | *Solving the elliptic equation $($with $z = 0. 118)$, so | ||
| + | :$$x^{\rm 2}+ y^{\rm 2} +\sqrt{\rm 2}\cdot \it x\cdot \it y - \it z = \rm 0.$$ | ||
| − | + | After solving the quadratic equation: | |
| − | + | :$$y_{\rm 1, \ 2}={\sqrt{\rm 2}}/ {\rm 2} \cdot x\pm\sqrt{{x^{\rm 2}}/{\rm 2}-x^{\rm 2}+{\it z}} | |
| − | :$$y_{\rm 1, \ 2}={\sqrt{\rm 2}}/ {\rm 2} \cdot | + | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm 1, \ 2}={\it x}/{\sqrt{\rm 2}}\pm \sqrt{z-{x^{\rm 2}}/{\rm 2}}.$$ |
| − | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} | + | *The vertical tangent results for the case that the two solutions $y_{\rm 1,\ \rm 2}$ are identical. That is: The root expression must result in zero. |
| − | * | + | *The solution for positive $x$ is then: $x_{\rm T}=\sqrt{\rm 2\cdot \it z}=\rm \rm 0.485.$ |
| − | * | + | *Inserted into the ellipse equation one obtains for the $y$–value of the tangent point: |
| − | * | ||
:$$x_{\rm T}^{\rm 2} + y_{\rm T}^{\rm 2} + \sqrt{2} \cdot x_{\rm T} \cdot y_{\rm T} - z = 0 | :$$x_{\rm T}^{\rm 2} + y_{\rm T}^{\rm 2} + \sqrt{2} \cdot x_{\rm T} \cdot y_{\rm T} - z = 0 | ||
| − | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 2 z + y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} - | + | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 2 z + y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} - z = 0$$ |
| − | :$$\Rightarrow \hspace{0.3cm}y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot | + | :$$\Rightarrow \hspace{0.3cm}y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} + z = 0 |
| − | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (y_{\rm T} + \sqrt{ z}) = | + | \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (y_{\rm T} + \sqrt{ z}) = 0\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm T} = -\sqrt{ z} = -0.343.$$ |
| − | * | + | *This gives $y_{\rm T}=-{x_{\rm T}}/{\sqrt{\rm 2}}. $ But this also means: The tangent point $(x_{\rm T}, y_{\rm T})$ lies exactly on the correlation line $y=K(x)=-{ x}/{\sqrt{\rm 2}}.$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 125: | Line 123: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^4.2 Gaussian 2D Random Variables^]] |
Latest revision as of 16:43, 10 April 2022
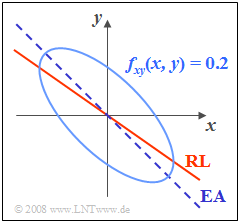
Given a two-dimensional Gaussian random variable $(x, y)$ with mean $(0, 0)$ and the 2D–PDF
- $$f_{xy}(x,\ y) = C\cdot{\rm e}^{-(x^{\rm 2} + y^{\rm 2} +\sqrt{\rm 2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm} y)}.$$
It is further known that the standard deviations are $\sigma_x=\sigma_y=1.$
Entered in the sketch are:
- a contour line of this PDF for $f_{xy}(x,y) =0.2$,
- the (dark blue) ellipse major axis $\rm (EA)$, and
- the (red) "correlation line" or "regression line" $\rm (RL)$.
Hints:
- The exercise belongs to the chapter Two-dimensional Gaussian Random Variables.
- More information on this topic is provided in the (German language) learning video "Gaußsche 2D-Zufallsgrößen":
- Part 1: Gaussian random variables without statistical bindings,
- Part 2: Gaussian random variables with statistical bindings.
Questions
Solution
(1) Even without specifying $\sigma_x = \sigma_y = 1$ one could see that the standard deviations $\sigma_x$ and $\sigma_y$ are equal,
since in the exponent of $f_{xy}(x, y)$ the coefficients at $x^2$ and $y^2$ are equal.
since in the exponent of $f_{xy}(x, y)$ the coefficients at $x^2$ and $y^2$ are equal.
- By comparing coefficients, we thus obtain:
- $$\frac{- 2 \rho_{xy}}{\sigma_x\cdot\sigma_y} = \sqrt{2}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \rho_{xy}=\frac{-1}{\sqrt{2}} \hspace{0.15cm}\underline{\approx -0.707}.$$
(2) Using the numerical values calculated in point (1), we obtain:
- $$C=\frac{\rm 1}{\rm 2\it\pi\cdot\sigma_x\cdot\sigma_y\cdot\sqrt{\rm 1 - \rho_{xy}^{\rm 2}}} =\frac{\rm 1}{\rm 2\pi\cdot\rm 1\cdot 1\cdot\sqrt{0.5}}=\frac{\rm 1}{\sqrt{\rm 2}\cdot \pi}\hspace{0.15cm}\underline{\approx \rm 0.225}.$$
(3) The general equation is:
- $$\alpha = {\rm 1}/{\rm 2}\cdot \rm arctan \ (\rm 2 \cdot\it \rho_{xy}\cdot \frac{\sigma_x\cdot\sigma_y}{\sigma_x^{\rm 2} - \sigma_y^{\rm 2}}{\rm ).}$$
- Applies $\sigma_x = \sigma_y$ and $\rho_{xy} \ne 0$, then the angle is always $\alpha = \pm 45^\circ$, where the sign is equal to the sign of $\rho_{xy}$.
- In the present case $\alpha\hspace{0.15cm}\underline{ = -45^\circ}$ holds.
(4) For the plotted contour line holds:
- $$f_{xy}(x, y)=\frac{1}{\sqrt{2}\cdot \pi}\cdot {\rm e}^{(x^{2} + y^{2} + \sqrt{2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm}y)}=0.2\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm e}^{-(x^{2} + y^{2} + \sqrt{2}\hspace{0.05cm} \cdot \hspace{0.05cm} x \hspace{0.05cm} \cdot \hspace{0.05cm}y)} = 0.8885 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x^{\rm 2} + y^{\rm 2} + \sqrt{\rm 2}\cdot\hspace{0.05cm} x \hspace{0.05cm} \cdot \hspace{0.05cm}y = -{\rm ln(0.8885)} \approx\rm 0.118.$$
- The angle of the ellipse major axis is $\alpha = -45^\circ$. Therefore $y_0 = - x_0$ must hold. It further follows:
- $$x_{\rm 0}^{\rm 2} + (-x_{\rm 0})^{\rm 2} + \sqrt{\rm 2}\cdot x_{\rm 0}(-x_{\rm 0}) = 0.118$$
- $$\Rightarrow \hspace{0.3cm}(\rm 2 - \sqrt{\rm 2})\cdot \it x_{\rm 0}^{\rm 2} = {\rm 0.118} \hspace{0.5cm}\rightarrow \hspace{0.5cm} x_{\rm 0}^{\rm 2} \approx \frac{\rm0.118}{\rm0.585}\approx\rm 0.202; \hspace{0.5cm} {\it x}_{\rm 0}\approx\pm\rm 0.450.$$
- The two intersections of the plotted contour lines with the ellipse major axis are thus at $(+0.45, -0.45)$ and $(-0.45, +0.45)$.
- The quotient in both cases is $x_0/y_0 \hspace{0.15cm}\underline{ = -1}$.
(5) Correct are the proposed solutions 2 and 3:
- With $\sigma_x = \sigma_y$ and the result of the subtask (1) holds for the angle of the correlation line:
- $$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x} = \arctan (\rho_{\it xy})=\arctan(-{\rm 1}/{\sqrt{\rm 2}})\approx -\rm 35.3^{\circ}.$$
- This means: The first statement is false and the second is true.
The following is the proof of the correctness of the last statement:
- Solving the elliptic equation $($with $z = 0. 118)$, so
- $$x^{\rm 2}+ y^{\rm 2} +\sqrt{\rm 2}\cdot \it x\cdot \it y - \it z = \rm 0.$$
After solving the quadratic equation:
- $$y_{\rm 1, \ 2}={\sqrt{\rm 2}}/ {\rm 2} \cdot x\pm\sqrt{{x^{\rm 2}}/{\rm 2}-x^{\rm 2}+{\it z}} \hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm 1, \ 2}={\it x}/{\sqrt{\rm 2}}\pm \sqrt{z-{x^{\rm 2}}/{\rm 2}}.$$
- The vertical tangent results for the case that the two solutions $y_{\rm 1,\ \rm 2}$ are identical. That is: The root expression must result in zero.
- The solution for positive $x$ is then: $x_{\rm T}=\sqrt{\rm 2\cdot \it z}=\rm \rm 0.485.$
- Inserted into the ellipse equation one obtains for the $y$–value of the tangent point:
- $$x_{\rm T}^{\rm 2} + y_{\rm T}^{\rm 2} + \sqrt{2} \cdot x_{\rm T} \cdot y_{\rm T} - z = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 2 z + y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} - z = 0$$
- $$\Rightarrow \hspace{0.3cm}y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} + z = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (y_{\rm T} + \sqrt{ z}) = 0\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm T} = -\sqrt{ z} = -0.343.$$
- This gives $y_{\rm T}=-{x_{\rm T}}/{\sqrt{\rm 2}}. $ But this also means: The tangent point $(x_{\rm T}, y_{\rm T})$ lies exactly on the correlation line $y=K(x)=-{ x}/{\sqrt{\rm 2}}.$