Difference between revisions of "Aufgaben:Exercise 1.6: Non-Binary Markov Sources"
m (Text replacement - "[[Informationstheorie" to "[[Information_Theory") |
|||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Discrete_Sources_with_Memory |
}} | }} | ||
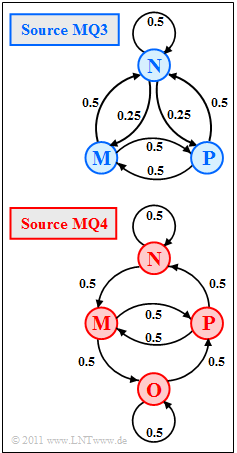
| − | [[File: | + | [[File:EN_Inf_A_1_6.png|right|frame|Markov sources with <br>$M = 3$ and $M = 4$]] |
| − | + | The graph shows two ergodic Markov sources $($German: "Markovquellen" ⇒ "$\rm MQ$"$)$: | |
| − | * | + | * The source $\rm MQ3$ is denoted by $M = 3$ states (symbols) $\rm N$, $\rm M$, $\rm P$. Due to stationarity, the probabilities have the following values: |
| − | :$$p_{\rm N} = | + | :$$p_{\rm N} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm M} = p_{\rm P} = 1/4\hspace{0.05cm}.$$ |
| − | * | + | * For the source $\rm MQ4$ the state $\rm O$ is additionally possible ⇒ $M = 4$. Due to the symmetric transitions, the stationary probabilities are all equal: |
| − | :$$p_{\rm N} = p_{\rm M} = p_{\rm O} = | + | :$$p_{\rm N} = p_{\rm M} = p_{\rm O} = p_{\rm P} = 1/4\hspace{0.05cm}.$$ |
| − | + | In terms of information theory, Markov sources are of particular importance, since with these – and only with these – by | |
| − | * $H_1$ | + | * $H_1$ (first entropy approximation, based only on the symbol probabilities), and |
| − | * $H_2$ ( | + | * $H_2$ (second entropy approximation, computable with the composite probabilities for all two-tuples) |
| − | + | are also determined at the same time: | |
| − | * | + | * the further entropy approximations $H_k$ with $k = 3, \ 4$, ..., and |
| − | * | + | * the actual (final) source entropy $H$. |
| − | + | The following equations of determination apply: | |
| − | :$$H = 2 \cdot H_2 - H_1\hspace{0.05cm},$$ | + | :$$H= H_{k \to \infty} = 2 \cdot H_2 - H_1\hspace{0.05cm},$$ |
:$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H \big ] | :$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H \big ] | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 32: | Line 32: | ||
| + | ''Hint:'' | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Discrete_Sources_with_Memory|Discrete Sources with Memory]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Discrete_Sources_with_Memory#Non-binary_Markov_sources|Non-binary Markov Sources]]. | ||
| + | *For all entropies, add the pseudo-unit "bit/symbol". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 45: | Line 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the entropy approximation $H_1$ of the Markov source $\rm MQ3$. |
|type="{}"} | |type="{}"} | ||
| − | $H_1 \ = \ $ | + | $H_1 \ = \ $ { 1.5 3% } $\ \rm bit/symbol$ |
| − | { | + | {Calculate the entropy approximation $H_2$ of the Markov source $\rm MQ3$. |
|type="{}"} | |type="{}"} | ||
| − | $H_2 \ = \ | + | $H_2 \ = \ $ { 1.375 3% } $\ \rm bit/symbol$ |
| − | { | + | {What are the actual source entropy $H= H_{k \to \infty}$ and the approximations $H_3$ and $H_4$ for $\rm MQ3$ ? |
|type="{}"} | |type="{}"} | ||
| − | $H \ = \ $ | + | $H \ = \ $ { 1.25 3% } $\ \rm bit/symbol$ |
| − | $H_3 \ = \ $ { 1.333 3% } $\ \rm bit/ | + | $H_3 \ = \ $ { 1.333 3% } $\ \rm bit/symbol$ |
| − | $H_4 \ = \ $ { 1.3125 3% } $\ \rm bit/ | + | $H_4 \ = \ $ { 1.3125 3% } $\ \rm bit/symbol$ |
| − | + | {Calculate the entropy approximation $H_1$ of the Markov source $\rm MQ4$. | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $H_1 \ = \ | + | $H_1 \ = \ $ { 2 3% } $\ \rm bit/symbol$ |
| − | { | + | {Calculate the entropy approximation $H_2$ of the Markov source $\rm MQ4$ |
|type="{}"} | |type="{}"} | ||
| − | $H_2 \ = | + | $H_2 \ = \ $ { 1.5 3% } $\ \rm bit/symbol$ |
| − | { | + | {What are the actual source entropy $H= H_{k \to \infty}$ and the approximations $H_3$ and $H_4$ for $\rm MQ4$ ? |
|type="{}"} | |type="{}"} | ||
| − | $H \ = | + | $H \ = \ $ { 1 3% } $\ \rm bit/symbol$ |
| − | $H_3 \ = | + | $H_3 \ = \ $ { 1.333 3% } $\ \rm bit/symbol$ |
| − | $H_4 \ = | + | $H_4 \ = \ $ { 1.25 3% } $\ \rm bit/symbol$ |
| − | |||
</quiz> | </quiz> | ||
| Line 83: | Line 79: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The symbol probabilities of the ternary Markov source are given. |
| − | * | + | *From this, the entropy approximation $H_1$ can be calculated: |
| − | :$$H_{\rm 1} | + | :$$H_{\rm 1} = 1/2 \cdot {\rm log}_2\hspace{0.1cm} (2) + 2 \cdot 1/4 \cdot {\rm log}_2\hspace{0.1cm}(4 ) \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The composite probability is $p_{\rm XY} = p_{\rm X} \cdot p_{\rm Y|X}$, where $p_{\rm X}$ gives the symbol probability of $\rm X$ and $p_{\rm Y|X}$ gives the conditional probability of $\rm Y$, given that previously $\rm X$ occurred. |
| − | *$\rm X$ | + | *$\rm X$ and $\rm Y$ are here placeholders for the symbols $\rm N$, $\rm P$ and $\rm M$. Then holds: |
:$$p_{\rm NN} = 1/2 \cdot 1/2 = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm PP} = 1/4 \cdot 0 = 0\hspace{0.05cm},\hspace{0.2cm}p_{\rm MM} = 1/4 \cdot 0 = 0 \hspace{0.05cm},$$ | :$$p_{\rm NN} = 1/2 \cdot 1/2 = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm PP} = 1/4 \cdot 0 = 0\hspace{0.05cm},\hspace{0.2cm}p_{\rm MM} = 1/4 \cdot 0 = 0 \hspace{0.05cm},$$ | ||
:$$ p_{\rm NP} = 1/2 \cdot 1/4 = 1/8\hspace{0.05cm},\hspace{0.2cm} p_{\rm PM} = 1/4 \cdot 1/2 = 1/8\hspace{0.05cm},\hspace{0.2cm}p_{\rm MN} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$ | :$$ p_{\rm NP} = 1/2 \cdot 1/4 = 1/8\hspace{0.05cm},\hspace{0.2cm} p_{\rm PM} = 1/4 \cdot 1/2 = 1/8\hspace{0.05cm},\hspace{0.2cm}p_{\rm MN} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$ | ||
| Line 101: | Line 97: | ||
| − | '''(3)''' $\rm MQ3$ | + | '''(3)''' $\rm MQ3$ has Markov properties. |
| − | * | + | * Therefore, from $H_1$ and $H_2$ all approximations $H_3$, $H_4$, ... and also the limit $H =H_\infty$ for $k \to \infty$ are given: |
| − | :$$H | + | :$$H = 2 \cdot H_2 - H_1 = 2\cdot 1.375 - 1.5 \hspace{0.15cm} \underline {= 1.250 \,{\rm bit/symbol}}\hspace{0.05cm},$$ |
| − | :$$ H_3 \hspace{0.1cm} = | + | :$$ H_3 \hspace{0.1cm} = \hspace{0.1cm}(H_1 + 2 \cdot H)/3 = (1.5 + 2 \cdot 1.25)/3 \hspace{0.15cm} \underline {= 1.333 \,{\rm bit/symbol}}\hspace{0.05cm},$$ |
| − | :$$ H_4 = (H_1 + 3 \cdot H)/4 = (1.5 + 3 \cdot 1.25)/4 \hspace{0.15cm} \underline {= 1.3125 \,{\rm bit/ | + | :$$ H_4 = (H_1 + 3 \cdot H)/4 = (1.5 + 3 \cdot 1.25)/4 \hspace{0.15cm} \underline {= 1.3125 \,{\rm bit/symbol}}\hspace{0.05cm}.$$ |
| − | * | + | *The tenth entropy approximation still differs from the final value $H = 1.25 \,\rm bit/symbol$, albeit only slightly $($by $2\%)$ : |
| − | :$$H_{10} = (H_1 + 9 \cdot H)/10 = (1.5 + 9 \cdot 1.25)/10 | + | :$$H_{10} = (H_1 + 9 \cdot H)/10 = (1.5 + 9 \cdot 1.25)/10 {= 1.275 \,{\rm bit/symbol}}\hspace{0.05cm}.$$ |
| − | '''(4)''' | + | '''(4)''' According to the specification, for $\rm MQ4$ the $M = 4$ symbols are equally probable. |
| − | * | + | *From this follows: |
| − | :$$H_{\rm 1} | + | :$$H_{\rm 1} = H_{\rm 0} = {\rm log}_2\hspace{0.1cm} (4) \hspace{0.15cm} \underline {= 2 \,{\rm bit/symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | '''(5)''' Of the $M^2 = 16$ possible two-tuples, eight combinations are now not possible: | ||
| + | :$$\rm NP, NO, PP, PO, OM, ON, MM, MN.$$ | ||
| − | + | *The eight other combinations (two-tuples) each yield the composite probability value $1/8$, as shown in two examples: | |
| − | :$$\rm | + | :$$p_{\rm NN} = p_{\rm N} \cdot p_{\rm N\hspace{0.01cm}|\hspace{0.01cm}N} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},\hspace{0.5cm} |
| + | p_{\rm MP} = p_{\rm M} \cdot p_{\rm P\hspace{0.01cm}|\hspace{0.01cm}M} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ 8 \cdot 1/8 \cdot {\rm log}_2\hspace{0.1cm} (8) \big ] \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(6)''' Because of the Markove property, here: | ||
| + | :$$H = 2 \cdot H_2 - H_1 = 2\cdot 1.5 - 2 \hspace{0.15cm} \underline {= 1 \,{\rm bit/symbol}}\hspace{0.05cm},$$ | ||
| + | :$$ H_3 = (H_1 + 2 \cdot H)/3 = (2 + 2 \cdot 1)/3 \hspace{0.15cm} \underline {= 1.333 \,{\rm bit/symbol}}\hspace{0.05cm},$$ | ||
| + | :$$ H_4 = (H_1 + 3 \cdot H)/4 = (2 + 3 \cdot 1)/4 \hspace{0.15cm} \underline {= 1.250 \,{\rm bit/symbol}}\hspace{0.05cm}.$$ | ||
| + | *Also here, the tenth approximation still differs significantly from the final value, namely by $10\%$: | ||
| + | :$$H_{10} = (H_1 + 9 \cdot H)/10 = (2 + 9 \cdot 1)/10 {= 1.1 \,{\rm bit/symbol}}\hspace{0.05cm}.$$ | ||
| + | *A deviation of only $2\%$ results here only for $k = 50$. For comparison: For the Markov source $\rm MQ3$ this approximation was already achieved with $k = 10$ . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.2 Sources with Memory^]] |
Latest revision as of 13:05, 10 August 2021
The graph shows two ergodic Markov sources $($German: "Markovquellen" ⇒ "$\rm MQ$"$)$:
- The source $\rm MQ3$ is denoted by $M = 3$ states (symbols) $\rm N$, $\rm M$, $\rm P$. Due to stationarity, the probabilities have the following values:
- $$p_{\rm N} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm M} = p_{\rm P} = 1/4\hspace{0.05cm}.$$
- For the source $\rm MQ4$ the state $\rm O$ is additionally possible ⇒ $M = 4$. Due to the symmetric transitions, the stationary probabilities are all equal:
- $$p_{\rm N} = p_{\rm M} = p_{\rm O} = p_{\rm P} = 1/4\hspace{0.05cm}.$$
In terms of information theory, Markov sources are of particular importance, since with these – and only with these – by
- $H_1$ (first entropy approximation, based only on the symbol probabilities), and
- $H_2$ (second entropy approximation, computable with the composite probabilities for all two-tuples)
are also determined at the same time:
- the further entropy approximations $H_k$ with $k = 3, \ 4$, ..., and
- the actual (final) source entropy $H$.
The following equations of determination apply:
- $$H= H_{k \to \infty} = 2 \cdot H_2 - H_1\hspace{0.05cm},$$
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H \big ] \hspace{0.05cm}.$$
Hint:
- The exercise belongs to the chapter Discrete Sources with Memory.
- Reference is made in particular to the page Non-binary Markov Sources.
- For all entropies, add the pseudo-unit "bit/symbol".
Fragebogen
Musterlösung
- From this, the entropy approximation $H_1$ can be calculated:
- $$H_{\rm 1} = 1/2 \cdot {\rm log}_2\hspace{0.1cm} (2) + 2 \cdot 1/4 \cdot {\rm log}_2\hspace{0.1cm}(4 ) \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(2) The composite probability is $p_{\rm XY} = p_{\rm X} \cdot p_{\rm Y|X}$, where $p_{\rm X}$ gives the symbol probability of $\rm X$ and $p_{\rm Y|X}$ gives the conditional probability of $\rm Y$, given that previously $\rm X$ occurred.
- $\rm X$ and $\rm Y$ are here placeholders for the symbols $\rm N$, $\rm P$ and $\rm M$. Then holds:
- $$p_{\rm NN} = 1/2 \cdot 1/2 = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm PP} = 1/4 \cdot 0 = 0\hspace{0.05cm},\hspace{0.2cm}p_{\rm MM} = 1/4 \cdot 0 = 0 \hspace{0.05cm},$$
- $$ p_{\rm NP} = 1/2 \cdot 1/4 = 1/8\hspace{0.05cm},\hspace{0.2cm} p_{\rm PM} = 1/4 \cdot 1/2 = 1/8\hspace{0.05cm},\hspace{0.2cm}p_{\rm MN} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},$$
- $$ p_{\rm NM} = 1/2 \cdot 1/4 = 1/8\hspace{0.05cm},\hspace{0.2cm} p_{\rm MP} = 1/4 \cdot 1/2 = 1/8\hspace{0.05cm},\hspace{0.2cm}p_{\rm PN} = 1/4 \cdot 1/2 = 1/8$$
- $$\Rightarrow \hspace{0.3cm} H_{\rm 2} = {1}/{2} \cdot \big [ 1/4 \cdot {\rm log}_2\hspace{0.1cm}( 4) + 6 \cdot 1/8 \cdot {\rm log}_2\hspace{0.1cm} (8) \big ] \hspace{0.15cm} \underline {= 1.375 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(3) $\rm MQ3$ has Markov properties.
- Therefore, from $H_1$ and $H_2$ all approximations $H_3$, $H_4$, ... and also the limit $H =H_\infty$ for $k \to \infty$ are given:
- $$H = 2 \cdot H_2 - H_1 = 2\cdot 1.375 - 1.5 \hspace{0.15cm} \underline {= 1.250 \,{\rm bit/symbol}}\hspace{0.05cm},$$
- $$ H_3 \hspace{0.1cm} = \hspace{0.1cm}(H_1 + 2 \cdot H)/3 = (1.5 + 2 \cdot 1.25)/3 \hspace{0.15cm} \underline {= 1.333 \,{\rm bit/symbol}}\hspace{0.05cm},$$
- $$ H_4 = (H_1 + 3 \cdot H)/4 = (1.5 + 3 \cdot 1.25)/4 \hspace{0.15cm} \underline {= 1.3125 \,{\rm bit/symbol}}\hspace{0.05cm}.$$
- The tenth entropy approximation still differs from the final value $H = 1.25 \,\rm bit/symbol$, albeit only slightly $($by $2\%)$ :
- $$H_{10} = (H_1 + 9 \cdot H)/10 = (1.5 + 9 \cdot 1.25)/10 {= 1.275 \,{\rm bit/symbol}}\hspace{0.05cm}.$$
(4) According to the specification, for $\rm MQ4$ the $M = 4$ symbols are equally probable.
- From this follows:
- $$H_{\rm 1} = H_{\rm 0} = {\rm log}_2\hspace{0.1cm} (4) \hspace{0.15cm} \underline {= 2 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(5) Of the $M^2 = 16$ possible two-tuples, eight combinations are now not possible:
- $$\rm NP, NO, PP, PO, OM, ON, MM, MN.$$
- The eight other combinations (two-tuples) each yield the composite probability value $1/8$, as shown in two examples:
- $$p_{\rm NN} = p_{\rm N} \cdot p_{\rm N\hspace{0.01cm}|\hspace{0.01cm}N} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm},\hspace{0.5cm} p_{\rm MP} = p_{\rm M} \cdot p_{\rm P\hspace{0.01cm}|\hspace{0.01cm}M} = 1/4 \cdot 1/2 = 1/8 \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ 8 \cdot 1/8 \cdot {\rm log}_2\hspace{0.1cm} (8) \big ] \hspace{0.15cm} \underline {= 1.5 \,{\rm bit/symbol}} \hspace{0.05cm}.$$
(6) Because of the Markove property, here:
- $$H = 2 \cdot H_2 - H_1 = 2\cdot 1.5 - 2 \hspace{0.15cm} \underline {= 1 \,{\rm bit/symbol}}\hspace{0.05cm},$$
- $$ H_3 = (H_1 + 2 \cdot H)/3 = (2 + 2 \cdot 1)/3 \hspace{0.15cm} \underline {= 1.333 \,{\rm bit/symbol}}\hspace{0.05cm},$$
- $$ H_4 = (H_1 + 3 \cdot H)/4 = (2 + 3 \cdot 1)/4 \hspace{0.15cm} \underline {= 1.250 \,{\rm bit/symbol}}\hspace{0.05cm}.$$
- Also here, the tenth approximation still differs significantly from the final value, namely by $10\%$:
- $$H_{10} = (H_1 + 9 \cdot H)/10 = (2 + 9 \cdot 1)/10 {= 1.1 \,{\rm bit/symbol}}\hspace{0.05cm}.$$
- A deviation of only $2\%$ results here only for $k = 50$. For comparison: For the Markov source $\rm MQ3$ this approximation was already achieved with $k = 10$ .