Difference between revisions of "Aufgaben:Exercise 4.3Z: Exponential and Laplace Distribution"
m (Text replacement - "[[Informationstheorie" to "[[Information_Theory") |
m (Text replacement - "value-continuous" to "continuous") |
||
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Differential_Entropy |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_Z_4_3.png|right|frame|Exponential PDF (above) d<br>Laplace PDF (below)]] |
| − | + | We consider here the probability density functions $\rm (PDF)$ of two continuous random variables: | |
| − | * | + | *The random variable $X$ is exponentially distributed (see top plot): For $x<0$ ⇒ $f_X(x) = 0$, and for positive $x$–values: |
:$$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$ | :$$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$ | ||
| − | * | + | * On the other hand, for the Laplace distributed random variable $Y$ in the whole range $ - \infty < y < + \infty$ holds (lower sketch): |
:$$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|\hspace{0.05cm}y\hspace{0.05cm}|}\hspace{0.05cm}.$$ | :$$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|\hspace{0.05cm}y\hspace{0.05cm}|}\hspace{0.05cm}.$$ | ||
| − | + | To be calculated are the differential entropies $h(X)$ and $h(Y)$ depending on the PDF parameter $\it \lambda$. For example: | |
:$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} | ||
\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [f_X(x) \big ] \hspace{0.1cm}{\rm d}x | \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [f_X(x) \big ] \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | If $\log_2$ is used, add the pseudo-unit "bit". | |
| − | In | + | In subtasks '''(2)''' and '''(4)''' specify the differential entropy in the following form: |
| − | :$$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \cdot \sigma^2) | + | :$$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \cdot \sigma^2), |
| − | \hspace{0. | + | \hspace{0.8cm}h(Y) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} \cdot \sigma^2) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Determine by which factor ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)}$ the exponential PDF is characterized and which factor ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)}$ results for the Laplace PDF. | |
| Line 30: | Line 30: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Differentielle_Entropie|Differential Entropy]]. |
| − | * | + | *Useful hints for solving this task can be found in particular on the page [[Information_Theory/Differentielle_Entropie#Differential_entropy_of_some_power-constrained_random_variables|Differential entropy of some power-constrained random variables]]. |
| − | * | + | *For the variance of the exponentially distributed random variable $X$ holds, as derived in [[Aufgaben:Exercise_4.1Z:_Calculation_of_Moments|Exercise 4.1Z]]: $\sigma^2 = 1/\lambda^2$. |
| − | * | + | *The variance of the Laplace distributed random variable $Y$ is twice as large for the same $\it \lambda$: $\sigma^2 = 2/\lambda^2$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the differential entropy of the exponential distribution for $\lambda = 1$. |
|type="{}"} | |type="{}"} | ||
$h(X) \ = \ $ { 1.443 3% } $\ \rm bit$ | $h(X) \ = \ $ { 1.443 3% } $\ \rm bit$ | ||
| − | { | + | {What is the characteristic ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)}$ for the exponential distribution corresponding to the form $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(X)} \cdot \sigma^2)$ ? |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \ = \ $ { 7.39 3% } | ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \ = \ $ { 7.39 3% } | ||
| − | { | + | {Calculate the differential entropy of the Laplace distribution for $\lambda = 1$. |
|type="{}"} | |type="{}"} | ||
$h(Y) \ = \ $ { 2.443 3% } $\ \rm bit$ | $h(Y) \ = \ $ { 2.443 3% } $\ \rm bit$ | ||
| − | { | + | {What is the characteristic ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)} $ for the Laplace distribution corresponding to the form $h(Y) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(Y)} \cdot \sigma^2)$? |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)} \ = \ $ { 14.78 3% } | ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)} \ = \ $ { 14.78 3% } | ||
| Line 64: | Line 64: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Although in this exercise the result should be given in "bit", we use the natural logarithm for derivation. |
| − | * | + | *Then the differential entropy is: |
:$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} | ||
\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \big [f_X(x)\big] \hspace{0.1cm}{\rm d}x | \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \big [f_X(x)\big] \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *For the exponential distribution, the integration limits are $0$ and $+∞$. In this range, the PDF $f_X(x)$ according to the specification sheet is used: |
:$$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} | :$$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} | ||
\lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | ||
| Line 82: | Line 82: | ||
\lambda \cdot x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x | \lambda \cdot x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | We can see: | |
| − | * | + | * The first integrand is identical to the PDF $f_X(x)$ considered here. Thus, the integral over the entire integration domain yields $1$. |
| − | * | + | * The second integral corresponds exactly to the definition of the mean value $m_1$ (moment of first order). For the exponential PDF, $m_1 = 1/λ$ holds. From this follows: |
:$$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = | :$$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = | ||
- \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) | - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *This result is to be given the additional unit "nat". Using $\log_2$ instead of $\ln$, we obtain the differential entropy in "bit": |
:$$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) | :$$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} | ||
| Line 97: | Line 97: | ||
| − | '''(2)''' | + | '''(2)''' Considering the equation $\sigma^2 = 1/\lambda^2$ valid for the exponential distribution, we can transform the result found in '''(1)''' as follows: |
: $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = | : $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = | ||
{1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) | {1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) | ||
| Line 103: | Line 103: | ||
{1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) | {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *A comparison with the required basic form $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(X)} \cdot \sigma^2)$ leads to the result: |
:$${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} | :$${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 109: | Line 109: | ||
| − | '''(3)''' | + | '''(3)''' For the Laplace distribution, we divide the integration domain into two subdomains: |
| − | * $Y$ | + | * $Y$ negative ⇒ proportion $h_{\rm neg}(Y)$, |
| − | * $Y$ | + | * $Y$ positive ⇒ proportion $h_{\rm pos}(Y)$. |
| − | + | The total differential entropy, taking into account $h_{\rm neg}(Y) = h_{\rm pos}(Y)$ is given by | |
:$$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$ | :$$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$ | ||
:$$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} | :$$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} | ||
| Line 125: | Line 125: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | If we again consider that the first integral gives the value $1$ (PDF area) and the second integral gives the mean value $m_1 = 1/\lambda$ we obtain: | |
:$$h(Y) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + 1 = | :$$h(Y) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + 1 = | ||
- \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (2{\rm e}/\lambda) | - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (2{\rm e}/\lambda) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Since the result is required in "bit", we still need to replace "$\ln$" by "$\log_2$": |
:$$h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}/\lambda) | :$$h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}/\lambda) | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} | ||
| Line 138: | Line 138: | ||
| − | '''(4)''' | + | '''(4)''' For the Laplace distribution, the relation $\sigma^2 = 2/\lambda^2$ holds. Thus, we obtain: |
:$$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = | :$$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = | ||
{1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) | {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) | ||
| Line 144: | Line 144: | ||
{1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} | {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Consequently, the ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}$ value is twice as large for the Laplace distribution as for the exponential distribution. |
| − | * | + | *Thus, the Laplace PDF is better than the exponential PDF in terms of differential entropy when power-limited signals are assumed. |
| − | * | + | *Under the constraint of peak limitation, both the exponential and Laplace PDF are completely unsuitable, as is the Gaussian PDF. These all extend to infinity. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 152: | Line 152: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.1 Differential Entropy^]] |
Latest revision as of 09:27, 11 October 2021
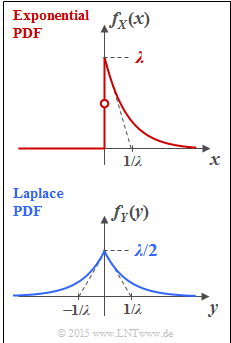
We consider here the probability density functions $\rm (PDF)$ of two continuous random variables:
- The random variable $X$ is exponentially distributed (see top plot): For $x<0$ ⇒ $f_X(x) = 0$, and for positive $x$–values:
- $$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}. $$
- On the other hand, for the Laplace distributed random variable $Y$ in the whole range $ - \infty < y < + \infty$ holds (lower sketch):
- $$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|\hspace{0.05cm}y\hspace{0.05cm}|}\hspace{0.05cm}.$$
To be calculated are the differential entropies $h(X)$ and $h(Y)$ depending on the PDF parameter $\it \lambda$. For example:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [f_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
If $\log_2$ is used, add the pseudo-unit "bit".
In subtasks (2) and (4) specify the differential entropy in the following form:
- $$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \cdot \sigma^2), \hspace{0.8cm}h(Y) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} \cdot \sigma^2) \hspace{0.05cm}.$$
Determine by which factor ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)}$ the exponential PDF is characterized and which factor ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)}$ results for the Laplace PDF.
Hints:
- The exercise belongs to the chapter Differential Entropy.
- Useful hints for solving this task can be found in particular on the page Differential entropy of some power-constrained random variables.
- For the variance of the exponentially distributed random variable $X$ holds, as derived in Exercise 4.1Z: $\sigma^2 = 1/\lambda^2$.
- The variance of the Laplace distributed random variable $Y$ is twice as large for the same $\it \lambda$: $\sigma^2 = 2/\lambda^2$.
Questions
Solution
- Then the differential entropy is:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \big [f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
- For the exponential distribution, the integration limits are $0$ and $+∞$. In this range, the PDF $f_X(x)$ according to the specification sheet is used:
- $$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x})\right ]\hspace{0.1cm}{\rm d}x - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
We can see:
- The first integrand is identical to the PDF $f_X(x)$ considered here. Thus, the integral over the entire integration domain yields $1$.
- The second integral corresponds exactly to the definition of the mean value $m_1$ (moment of first order). For the exponential PDF, $m_1 = 1/λ$ holds. From this follows:
- $$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.05cm}.$$
- This result is to be given the additional unit "nat". Using $\log_2$ instead of $\ln$, we obtain the differential entropy in "bit":
- $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}) = \frac{{\rm ln} \hspace{0.1cm} ({\rm e})}{{\rm ln} \hspace{0.1cm} (2)} \hspace{0.15cm}\underline{= 1.443\,{\rm bit}} \hspace{0.05cm}.$$
(2) Considering the equation $\sigma^2 = 1/\lambda^2$ valid for the exponential distribution, we can transform the result found in (1) as follows:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = {1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) \hspace{0.05cm}.$$
- A comparison with the required basic form $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(X)} \cdot \sigma^2)$ leads to the result:
- $${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} \hspace{0.05cm}.$$
(3) For the Laplace distribution, we divide the integration domain into two subdomains:
- $Y$ negative ⇒ proportion $h_{\rm neg}(Y)$,
- $Y$ positive ⇒ proportion $h_{\rm pos}(Y)$.
The total differential entropy, taking into account $h_{\rm neg}(Y) = h_{\rm pos}(Y)$ is given by
- $$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y) $$
- $$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda/2) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y})\right ]\hspace{0.1cm}{\rm d}y = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot y \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
If we again consider that the first integral gives the value $1$ (PDF area) and the second integral gives the mean value $m_1 = 1/\lambda$ we obtain:
- $$h(Y) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (2{\rm e}/\lambda) \hspace{0.05cm}.$$
- Since the result is required in "bit", we still need to replace "$\ln$" by "$\log_2$":
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}) \hspace{0.15cm}\underline{= 2.443\,{\rm bit}} \hspace{0.05cm}.$$
(4) For the Laplace distribution, the relation $\sigma^2 = 2/\lambda^2$ holds. Thus, we obtain:
- $$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} \hspace{0.05cm}.$$
- Consequently, the ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}$ value is twice as large for the Laplace distribution as for the exponential distribution.
- Thus, the Laplace PDF is better than the exponential PDF in terms of differential entropy when power-limited signals are assumed.
- Under the constraint of peak limitation, both the exponential and Laplace PDF are completely unsuitable, as is the Gaussian PDF. These all extend to infinity.