Difference between revisions of "Aufgaben:Exercise 3.2: Spectrum with Angle Modulation"
m (Text replacement - "[[Modulationsverfahren" to "[[Modulation_Methods") |
|||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Phase_Modulation_(PM) |
}} | }} | ||
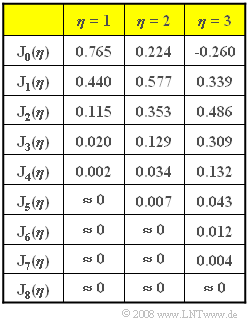
| − | [[File:P_ID1081__Mod_A_3_2.png|right|frame| | + | [[File:P_ID1081__Mod_A_3_2.png|right|frame|Table of Bessel functions]] |
| − | + | The following equations are assumed here: | |
| − | * | + | * Source signal: |
:$$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | :$$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$ | ||
| − | * | + | * Transmitted signal: |
:$$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$ | :$$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$ | ||
| − | * | + | * Received signal (ideal channel): |
:$$r(t) = s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t)\big ]\hspace{0.05cm},$$ | :$$r(t) = s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t)\big ]\hspace{0.05cm},$$ | ||
| − | * | + | * ideal demodulator: |
:$$ v(t) = \frac{1}{ K_{\rm M}} \cdot \phi(t)\hspace{0.05cm}.$$ | :$$ v(t) = \frac{1}{ K_{\rm M}} \cdot \phi(t)\hspace{0.05cm}.$$ | ||
| − | + | The graphs shows the $n$–th order Bessel functions of the first kind ${\rm J}_n (\eta)$ in table form. | |
| Line 23: | Line 23: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Phase_Modulation_(PM)|Phase Modulation]]. |
| − | * | + | *Particular reference is made to the pages [[Modulation_Methods/Phasenmodulation_(PM)#Spectral_function_of_a_phase-modulated_sine_signal|Spectral function of a phase-modulated sine signal]] and [[Modulation_Methods/Phase_Modulation_(PM)#Interpretation_of_the_Bessel_spectrum|Interpretation of the Bessel spectrum]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which modulation method is used here? |
|type="()"} | |type="()"} | ||
| − | - | + | - Amplitude modulation. |
| − | + | + | + Phase modulation. |
| − | - | + | - Frequency modulation. |
| − | { | + | {Which modulation method would you choose if the channel bandwidth was only $B_{\rm K} = 10 \ \rm kHz$ ? |
|type="()"} | |type="()"} | ||
| − | + | + | + Amplitude modulation. |
| − | - | + | - Phase modulation. |
| − | - | + | - Frequency modulation. |
| − | { | + | {How should one choose the modulator constant $K_{\rm M}$ for a phase deviation of $η = 1$ ? |
|type="{}"} | |type="{}"} | ||
$K_{\rm M} \ = \ $ { 0.5 3% } $\ \rm 1/V$ | $K_{\rm M} \ = \ $ { 0.5 3% } $\ \rm 1/V$ | ||
| − | { | + | {Calculate the spectrum $S_{\rm TP}(f)$ of the equivalent low-pass signal $s_{\rm TP}(t)$. |
| − | + | What are the weights of the spectral lines at $f = 0$ and $f = -3 \ \rm kHz$? | |
|type="{}"} | |type="{}"} | ||
$S_{\rm TP}(f = 0)\ = \ $ { 0.765 3% } $\ \rm V$ | $S_{\rm TP}(f = 0)\ = \ $ { 0.765 3% } $\ \rm V$ | ||
$S_{\rm TP}(f = -3\ \rm kHz) \ = \ $ { -0.453--0.427 } $\ \rm V$ | $S_{\rm TP}(f = -3\ \rm kHz) \ = \ $ { -0.453--0.427 } $\ \rm V$ | ||
| − | { | + | {Calculate the spectra of the analytical signal $s_{\rm +}(t)$ and the physical signal $s(t)$. What are the weights of the spectral lines at $f = 97 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$S_+(f = 97 \ \rm kHz)\ = \ $ { -0.453--0.427 } $\ \rm V$ | $S_+(f = 97 \ \rm kHz)\ = \ $ { -0.453--0.427 } $\ \rm V$ | ||
| Line 60: | Line 60: | ||
| − | { | + | {What is the required channel bandwidth $B_{\rm K}$ for $ η = 1$, if one ignores pulse weights smaller (in magnitude) than $0.01$ ? |
|type="{}"} | |type="{}"} | ||
$η = 1\text{:} \ \ \ B_{\rm K}\ = \ $ { 18 3% } $\ \rm kHz$ | $η = 1\text{:} \ \ \ B_{\rm K}\ = \ $ { 18 3% } $\ \rm kHz$ | ||
| − | { | + | {What would be the channel bandwidths for $η = 2$ and $η = 3$ ? |
|type="{}"} | |type="{}"} | ||
$η = 2\text{:} \ \ \ B_{\rm K}\ = \ $ { 24 3% } $\ \rm kHz$ | $η = 2\text{:} \ \ \ B_{\rm K}\ = \ $ { 24 3% } $\ \rm kHz$ | ||
| Line 71: | Line 71: | ||
</quiz> | </quiz> | ||
| − | + | ===Solution=== | |
| − | === | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The phase $ϕ(t)$ is proportional to the source signal $q(t)$ ⇒ this is a phase modulation ⇒ <u>Answer 2</u>. |
| − | '''(2)''' | + | '''(2)''' An angle modulation (PM, FM) always results in nonlinear distortion when the channel is bandlimited. |
| − | * | + | *In contrast, double-sideband amplitude modulation (DSB-AM) here enables distortion-free transmission with $B_{\rm K} = 6 \ \rm kHz$ ; ⇒ <u>Answer 1</u>. |
| − | '''(3)''' | + | '''(3)''' The modulation index (or phase deviation) is equal to $η = K_{\rm M} · A_{\rm N}$ for phase modulation. |
| − | * | + | *Thus, the modulator constant must be set to $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ to give $η = 1$ . |
| − | '''(4)''' | + | '''(4)''' A so-called Bessel spectrum is present: |
:$$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$ | :$$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$ | ||
| − | * | + | *This is a discrete spectrum with components at $f = n · f_{\rm N}$, where $n$ is an integer. |
| − | * | + | *The weights of the Dirac functions are given by the Bessel functions. When $A_{\rm T} = 1\ \rm V$ , one obtains: |
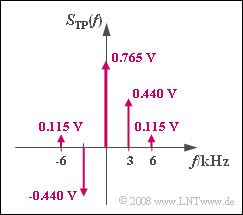
| − | [[File:P_ID1082__Mod_A_3_2_d.png|right|frame| | + | [[File:P_ID1082__Mod_A_3_2_d.png|right|frame|PM spectrum in the equivalent low-pass range]] |
:$$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$ | :$$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$ | ||
:$$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$ | :$$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$ | ||
:$$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$ | :$$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$ | ||
| − | * | + | *Due to the symmetry ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ , the spectral line at $f = -3 \ \rm kHz$ is obtained as: |
:$$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$ | :$$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$ | ||
| − | '' | + | ''Note'': For the spectral value at $f = 0$ we should actually write: |
:$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | :$$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$ | ||
| − | * | + | *This is therefore infinite due to the Dirac function, and only the weight of the Dirac function is finite. |
| − | * | + | *The same applies for all discrete spectral lines. |
| − | '''(5)''' $S_+(f)$ | + | '''(5)''' $S_+(f)$ is obtained from $S_{\rm TP}(f)$ by shifting $f_{\rm T}$ to the right. Therefore |
:$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | :$$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The actual spectrum differs from $S_+(f)$ by a factor of $1/2$ at positive frequencies: |
:$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | :$$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$ | ||
| − | * | + | *In general, we can write: |
:$$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$ | :$$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$ | ||
| − | '''(6)''' | + | '''(6)''' Under the suggested conditions, all the Bessel lines ${\rm J}_{|n|>3}$ can be disregarded. |
| − | * | + | * This gives $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$. |
| − | '''(7)''' | + | '''(7)''' The numerical values in the table given on the exercise page show that the following channel bandwidths would now be required: |
*für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$, | *für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$, | ||
*für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$. | *für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$. | ||
| Line 127: | Line 126: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^3.1 Phase Modulation^]] |
Latest revision as of 16:21, 23 January 2023
The following equations are assumed here:
- Source signal:
- $$q(t) = 2\,{\rm V} \cdot \sin(2 \pi \cdot 3\,{\rm kHz} \cdot t)\hspace{0.05cm},$$
- Transmitted signal:
- $$s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + K_{\rm M} \cdot q(t)\big ]\hspace{0.05cm},$$
- Received signal (ideal channel):
- $$r(t) = s(t) = 1\,{\rm V} \cdot \cos\hspace{-0.1cm}\big[2 \pi \cdot 100\,{\rm kHz} \cdot t + \phi(t)\big ]\hspace{0.05cm},$$
- ideal demodulator:
- $$ v(t) = \frac{1}{ K_{\rm M}} \cdot \phi(t)\hspace{0.05cm}.$$
The graphs shows the $n$–th order Bessel functions of the first kind ${\rm J}_n (\eta)$ in table form.
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the pages Spectral function of a phase-modulated sine signal and Interpretation of the Bessel spectrum.
Questions
Solution
(2) An angle modulation (PM, FM) always results in nonlinear distortion when the channel is bandlimited.
- In contrast, double-sideband amplitude modulation (DSB-AM) here enables distortion-free transmission with $B_{\rm K} = 6 \ \rm kHz$ ; ⇒ Answer 1.
(3) The modulation index (or phase deviation) is equal to $η = K_{\rm M} · A_{\rm N}$ for phase modulation.
- Thus, the modulator constant must be set to $K_{\rm M} = 1/A_{\rm N}\hspace{0.15cm}\underline { = 0.5 \rm \cdot {1}/{V}}$ to give $η = 1$ .
(4) A so-called Bessel spectrum is present:
- $$ S_{\rm TP}(f) = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f - n \cdot f_{\rm N})\hspace{0.05cm}.$$
- This is a discrete spectrum with components at $f = n · f_{\rm N}$, where $n$ is an integer.
- The weights of the Dirac functions are given by the Bessel functions. When $A_{\rm T} = 1\ \rm V$ , one obtains:
- $$ S_{\rm TP}(f = 0) = A_{\rm T} \cdot {\rm J}_0 (\eta = 1) \hspace{0.15cm}\underline {= 0.765\,{\rm V}},$$
- $$ S_{\rm TP}(f = f_{\rm N}) = A_{\rm T} \cdot {\rm J}_1 (\eta = 1)\hspace{0.15cm} = 0.440\,{\rm V},$$
- $$ S_{\rm TP}(f = 2 \cdot f_{\rm N}) = A_{\rm T} \cdot {\rm J}_2 (\eta = 1) = 0.115\,{\rm V} \hspace{0.05cm}.$$
- Due to the symmetry ${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)$ , the spectral line at $f = -3 \ \rm kHz$ is obtained as:
- $$S_{\rm TP}(f = -f_{\rm N}) = -S_{\rm TP}(f = +f_{\rm N}) =\hspace{-0.01cm}\underline { -0.440\,{\rm V} \hspace{0.05cm}}.$$
Note: For the spectral value at $f = 0$ we should actually write:
- $$S_{\rm TP}(f = 0) = 0.765\,{\rm V} \cdot \delta (f) \hspace{0.05cm}.$$
- This is therefore infinite due to the Dirac function, and only the weight of the Dirac function is finite.
- The same applies for all discrete spectral lines.
(5) $S_+(f)$ is obtained from $S_{\rm TP}(f)$ by shifting $f_{\rm T}$ to the right. Therefore
- $$S_{\rm +}(f = 97\,{\rm kHz}) = S_{\rm TP}(f = -3\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.440\,{\rm V}} \hspace{0.05cm}.$$
- The actual spectrum differs from $S_+(f)$ by a factor of $1/2$ at positive frequencies:
- $$S(f = 97\,{\rm kHz}) = {1}/{2} \cdot S_{\rm +}(f = 97\,{\rm kHz}) \hspace{0.15cm}\underline {=-0.220\,{\rm V}} \hspace{0.05cm}.$$
- In general, we can write:
- $$ S(f) = \frac{A_{\rm T}}{2} \cdot \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot \delta (f \pm (f_{\rm T}+ n \cdot f_{\rm N}))\hspace{0.05cm}.$$
(6) Under the suggested conditions, all the Bessel lines ${\rm J}_{|n|>3}$ can be disregarded.
- This gives $B_{\rm K} = 2 · 3 · f_{\rm N}\hspace{0.15cm}\underline { = 18 \ \rm kHz}$.
(7) The numerical values in the table given on the exercise page show that the following channel bandwidths would now be required:
- für $η = 2$: $B_{\rm K} \hspace{0.15cm}\underline { = 24 \ \rm kHz}$,
- für $η = 3$: $B_{\rm K} \hspace{0.15cm}\underline { = 36 \ \rm kHz}$.