Difference between revisions of "Aufgaben:Exercise 3.9Z: Convolution of Gaussian Pulses"
From LNTwww
m (Text replacement - "Category:Aufgaben zu Signaldarstellung" to "Category:Exercises for Signal Representation") |
|||
| (7 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal Representation/The Convolution Theorem and Operation |
}} | }} | ||
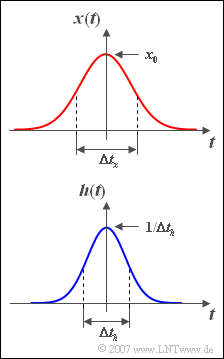
| − | [[File:P_ID544__Sig_Z_3_9.png|right|frame| | + | [[File:P_ID544__Sig_Z_3_9.png|right|frame|Gaussian pulses $x(t)$, $h(t)$]] |
| − | + | The convolution result of two Gaussian functions is to be determined. We consider | |
| + | *a Gaussian input pulse ${x(t)}$ with amplitude $x_0 = 1\,\text{V}$ and "equivalent pulse duration" $\Delta t_x = 4 \,\text{ms}$, as well as | ||
| + | *a likewise Gaussian impulse response ${h(t)}$, which has the "equivalent pulse duration" $\Delta t_h = 3 \,\text{ms}$ : | ||
:$$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$ | :$$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$ | ||
:$$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$ | :$$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$ | ||
| − | + | The output signal ${y(t)} = {x(t)} ∗{h(t)}$ is sought, whereby the diversions via the spectral functions is to be taken. | |
| Line 13: | Line 15: | ||
| − | '' | + | |
| − | * | + | ''Hint:'' |
| + | *This exercise belongs to the chapter [[Signal_Representation/The_Convolution_Theorem_and_Operation|The Convolution Theorem and Operation]]. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Give the spectral functions ${X(f)}$ and ${H(f)}$ an. Which values result for $f = 0$? |
|type="{}"} | |type="{}"} | ||
$X(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | $X(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | ||
| Line 28: | Line 31: | ||
| − | { | + | {Calculate the spectral function ${Y(f)}$ of the output signal. What is the spectral value at $f = 0$? |
|type="{}"} | |type="{}"} | ||
$Y(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | $Y(f = 0)\ = \ $ { 4 3% } $\text{mV/Hz}$ | ||
| − | { | + | {Calculate the output pulse ${y(t)}$. What values result for the amplitude $y_0 = y(t = 0)$ and the equivalent pulse duration $\Delta t_y$? |
|type="{}"} | |type="{}"} | ||
$y_0\ = \ $ { 0.8 3% } $\text{V}$ | $y_0\ = \ $ { 0.8 3% } $\text{V}$ | ||
| Line 42: | Line 45: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' By Fourier transformation one obtains: |
:$$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \hspace{0.05cm}\cdot \hspace{0.05cm}f} \right)^2 } .$$ | :$$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \hspace{0.05cm}\cdot \hspace{0.05cm}f} \right)^2 } .$$ | ||
| − | * | + | *The values we are looking for are |
| − | :$$X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}}, | + | :$$X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}}, \hspace{0.5cm} |
| − | + | H(f = 0)\; \underline{= 1}.$$ | |
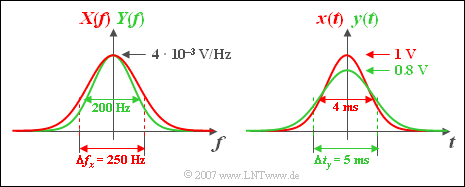
| − | [[File:P_ID589__Sig_Z_3_9_b_neu.png|right|frame| | + | [[File:P_ID589__Sig_Z_3_9_b_neu.png|right|frame|Gaussian spektra $X(f)$, $Y(f)$ – Gaussian pulses $x(t)$, $y(t)$]] |
| − | '''(2)''' | + | '''(2)''' Convolution in time domain corresponds to multiplication in frequency domain: |
:$$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$ | :$$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$ | ||
| − | * | + | *With the abbreviation $\Delta t_y = (\Delta t_x^2 + \Delta t_h^2)^{1/2} = 5\, \text{ms}$ one can write for this: |
:$$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } .$$ | :$$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } .$$ | ||
| − | * | + | *At frequency $f = 0$ , the spectral values at the input and output of the Gaussian filter are equal, so: |
:$$Y(f = 0) \;\underline{= 4 \text{ mV/Hz}}.$$ | :$$Y(f = 0) \;\underline{= 4 \text{ mV/Hz}}.$$ | ||
| − | * | + | *The function curve of ${Y(f)}$ is narrower than ${X(f)}$ and narrower than ${H(f)}$. |
| − | '''(3)''' | + | '''(3)''' The following Fourier correspondence holds: |
:$${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | :$${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | ||
| − | * | + | *This gives: |
:$$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | :$$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$ | ||
| − | * | + | *The maximum value of the signal ${y(t)}$ is also at $t = 0$ and is $y_0 \hspace{0.15cm}\underline{= 0.8 \text{ V} }$. |
| − | * | + | *The equivalent pulse duration results in $\Delta t_y \hspace{0.15cm}\underline{= 5 \text{ ms}}$ (see above graphic, right sketch). |
| − | * | + | *This means: The Gaussian ${H(f)}$ causes the output pulse ${y(t)}$ to be smaller and wider than the input pulse ${x(t)}$ . |
| − | * | + | *The pulse shape remains Gaussian. Because: '''Gaussian convoluted with Gaussian always results in Gaussian!''' |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.4 The Convolution Theorem^]] |
Latest revision as of 15:45, 29 April 2021
The convolution result of two Gaussian functions is to be determined. We consider
- a Gaussian input pulse ${x(t)}$ with amplitude $x_0 = 1\,\text{V}$ and "equivalent pulse duration" $\Delta t_x = 4 \,\text{ms}$, as well as
- a likewise Gaussian impulse response ${h(t)}$, which has the "equivalent pulse duration" $\Delta t_h = 3 \,\text{ms}$ :
- $$x( t ) = x_0 \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_x } )^2 } ,$$
- $$h( t ) = \frac{1}{\Delta t_h } \cdot {\rm{e}}^{ - {\rm{\pi }}( {t/\Delta t_h } )^2 } .$$
The output signal ${y(t)} = {x(t)} ∗{h(t)}$ is sought, whereby the diversions via the spectral functions is to be taken.
Hint:
- This exercise belongs to the chapter The Convolution Theorem and Operation.
Questions
Solution
(1) By Fourier transformation one obtains:
- $$X( f ) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } , \hspace{0.5cm}H(f) = {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_h \hspace{0.05cm}\cdot \hspace{0.05cm}f} \right)^2 } .$$
- The values we are looking for are
- $$X(f = 0)\;\underline{ = 4 \,\text{mV/Hz}}, \hspace{0.5cm} H(f = 0)\; \underline{= 1}.$$
(2) Convolution in time domain corresponds to multiplication in frequency domain:
- $$Y(f) = X(f) \cdot H(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_x^2 + \Delta t_h^2 } \right)f^2 } .$$
- With the abbreviation $\Delta t_y = (\Delta t_x^2 + \Delta t_h^2)^{1/2} = 5\, \text{ms}$ one can write for this:
- $$Y(f) = x_0 \cdot \Delta t_x \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 } .$$
- At frequency $f = 0$ , the spectral values at the input and output of the Gaussian filter are equal, so:
- $$Y(f = 0) \;\underline{= 4 \text{ mV/Hz}}.$$
- The function curve of ${Y(f)}$ is narrower than ${X(f)}$ and narrower than ${H(f)}$.
(3) The following Fourier correspondence holds:
- $${\rm{e}}^{ - {\rm{\pi }}\left( {\Delta t_y \hspace{0.05cm}\cdot \hspace{0.05cm} f} \right)^2 }\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{1}{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$
- This gives:
- $$y(t) = x(t) * h(t) = x_0 \cdot \frac{\Delta t_x }{\Delta t_y } \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_y } \right)^2 } .$$
- The maximum value of the signal ${y(t)}$ is also at $t = 0$ and is $y_0 \hspace{0.15cm}\underline{= 0.8 \text{ V} }$.
- The equivalent pulse duration results in $\Delta t_y \hspace{0.15cm}\underline{= 5 \text{ ms}}$ (see above graphic, right sketch).
- This means: The Gaussian ${H(f)}$ causes the output pulse ${y(t)}$ to be smaller and wider than the input pulse ${x(t)}$ .
- The pulse shape remains Gaussian. Because: Gaussian convoluted with Gaussian always results in Gaussian!