Difference between revisions of "Aufgaben:Exercise 3.5: Differentiation of a Triangular Pulse"
From LNTwww
m (Text replacement - "Signal_Representation/Gesetzmäßigkeiten_der_Fouriertransformation" to "Signal_Representation/Fourier_Transform_Laws") |
|||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fourier_Transform_Laws |
}} | }} | ||
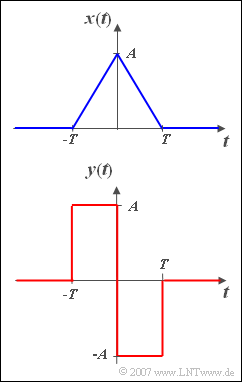
| − | [[File:P_ID514__Sig_A_3_5.png|250px|right|frame| | + | [[File:P_ID514__Sig_A_3_5.png|250px|right|frame|Triangular signal and <br>differentiated triangular signal]] |
| − | + | We are looking for the spectrum $Y(f)$ of the signal | |
| − | :$$y\left( t \right) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f | + | :$$y\left( t \right) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f or}}} \\ {{\rm{for}}} \\ \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {{\rm{else}}{\rm{.}}} \\\end{array}$$ |
| − | + | Let $A = 1\,{\rm V}$ and $T = 0.5\,{\rm ms}$ apply. | |
| − | + | The Fourier transform of the triangular pulse $x(t)$ sketched above is assumed to be known, namely | |
:$$X( f ) = A \cdot T \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }}fT} ),$$ | :$$X( f ) = A \cdot T \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }}fT} ),$$ | ||
| − | + | where $\text{si}(x) = \text{sin}(x)/x$. | |
| − | + | A comparison of the two signals shows that the following relationship exists between the functions $x(t)$ and $y(t)$ : | |
:$$y(t) = T \cdot \frac{{{\rm d}x(t)}}{{{\rm d}t}}.$$ | :$$y(t) = T \cdot \frac{{{\rm d}x(t)}}{{{\rm d}t}}.$$ | ||
| Line 28: | Line 28: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This task belongs to the chapter [[Signal_Representation/Fourier_Transform_Theorems|Fourier Transform Theorems]]. |
| − | * | + | *All the laws presented here - including the [[Signal_Representation/Fourier_Transform_Laws#Shifting_Theorem|Shifting Theorem]] and the [[Signal_Representation/Fourier_Transform_Theorems#Differentiation_Theorem|Differentiation Theorem]] – are illustrated with examples in the (German language) learning video<br> [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] ⇒ "Regularities to the Fourier transform". |
| − | *In | + | *In subtask '''(3)''' the spectrum $Y(f)$ is to be calculated starting from a symmetrical rectangular pulse $r(t)$ with amplitude $A$ and duration $T$ and its spectrum $R(f) = A \cdot T \cdot \text{si}(\pi fT)$ . This is achieved by applying the [[Signal_Representation/Fourier_Transform_Laws#Shifting_Theorem|Shifting Theorem]]. |
| − | *In [[Aufgaben:3.5Z_Integration_von_Diracfunktionen| | + | *In [[Aufgaben:3.5Z_Integration_von_Diracfunktionen|Exercise 3.5Z]] the spectrum $Y(f)$ is calculated starting from a signal consisting of three Dirac functions by applying the [[Signal_Representation/Fourier_Transform_Theorems#Integration_Theorem|Integration Theorem]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the spectral function $Y(f)$ at the output. What is its magnitude at the frequencies $f = 0$ and $f = 1 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$|Y(f=0)| \hspace{0.2cm} = \ $ { 0. } $\text{mV/Hz}$ | $|Y(f=0)| \hspace{0.2cm} = \ $ { 0. } $\text{mV/Hz}$ | ||
$|Y(f=1 \ \text{kHz})| \ = \ $ { 0.636 3% } $\text{mV/Hz}$ | $|Y(f=1 \ \text{kHz})| \ = \ $ { 0.636 3% } $\text{mV/Hz}$ | ||
| − | { | + | {Which statements are true regarding the spectrum $Y(f)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The zeros of $X(f)$ also remain in $Y(f)$ . |
| − | - | + | - For large $f$–values, $Y(f)$ satisfies the same bound as $X(f)$. |
| − | + | + | + For large $f$–values, $|X(f)|$ is smaller than the magnitude spectrum of a rectangular pulse of duration $T$. |
| − | { | + | {Calculate $Y(f)$ starting from the rectangular pulse by applying the displacement theorem. Which statement is true here? |
|type="()"} | |type="()"} | ||
| − | + | + | + The differentiation theorem leads to the result more quickly. |
| − | - | + | - The shifting theorem leads to the result more quickly. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The differentiation theorem reads generally: |
:$$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$ | :$$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$ | ||
| − | * | + | *Applied to the present example, one obtains: |
:$$Y( f ) = T \cdot {\rm{j}}\cdot 2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$ | :$$Y( f ) = T \cdot {\rm{j}}\cdot 2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$ | ||
| − | * | + | *This function is purely imaginary. At the frequency $f = 0$ the imaginary part also disappears. This can be formally proven, for example, by applying l'Hospital's rule ⇒ $Y( f = 0 ) \;\underline{= 0}$. |
| − | * | + | *However, the result also follows from the fact that the spectral value at $f = 0$ is equal to the integral over the time function $y(t)$ . |
| − | * | + | *At the normalised frequency $f \cdot T = 0.5$ $($i.e for $f = 1\,\text{ kHz})$ the sine function is equal to $1$ and we obtain $|Y(f = 1 \,\text{kHz})| = 4/\pi \cdot A \cdot T$, i.e. approximately $|Y(f=1 \ \text{kHz})| \ \underline{=0.636 \,\text{ mV/Hz}}$ (positive imaginary). |
| − | '''(2)''' | + | '''(2)''' The correct solutions are <u>1 and 3</u>: |
| − | * | + | *The zeros of $X(f)$ remain and there is another zero at the frequency $f = 0$. |
| − | * | + | *The upper bound is called the asymptotic curve |
:$$\left| {Y_{\max }( f )} \right| = \frac{2A}{{{\rm{\pi }} \cdot |f|}} \ge \left| {Y( f )} \right|.$$ | :$$\left| {Y_{\max }( f )} \right| = \frac{2A}{{{\rm{\pi }} \cdot |f|}} \ge \left| {Y( f )} \right|.$$ | ||
| − | * | + | *For the frequencies at which the sine function delivers the values $\pm 1$ , $|Y_{\text{max}}(f)|$ and $|Y(f)|$ are identical. |
| − | * | + | *For the rectangular pulse of same amplitude $A$ the corresponding bound is $A/(\pi \cdot |f|)$. |
| − | * | + | *In contrast, the spectrum $X(f)$ of the triangular pulse falls asymptotically faster: |
:$$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$ | :$$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$ | ||
| − | * | + | *This is due to the fact that $x(t)$ has no discontinuity points. |
| − | '''(3)''' | + | '''(3)''' Starting from a symmetrical rectangular pulse $r(t)$ with amplitude $A$ and duration $T$ the signal $y(t)$ can also be represented as follows: |
:$$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$ | :$$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$ | ||
| − | * | + | *By applying the shifting theorem twice, one obtains: |
:$$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$ | :$$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$ | ||
| − | * | + | *Using the relation $\text{e}^{\text{j}x} – \text{e}^{–\text{j}x} = 2\text{j} \cdot \text{sin}(x)$ it is also possible to write for this: |
:$$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$ | :$$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$ | ||
| − | * | + | *Consequently, the result is the same as in subtask '''(1)'''. |
| − | * | + | *Which way leads faster to the result, everyone must decide for himself. The author thinks that the first way is somewhat more favourable. |
| − | *<u> | + | *<u>Subjectively, we decide in favour of solution suggestion 1</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.3 Fourier Transform Theorems^]] |
Latest revision as of 14:19, 24 May 2021
We are looking for the spectrum $Y(f)$ of the signal
- $$y\left( t \right) = \left\{ \begin{array}{c} A \\ - A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {{\rm{f or}}} \\ {{\rm{for}}} \\ \\ \end{array}\;\begin{array}{*{20}c} { - T \le t < 0,} \\ {0 < t \le T,} \\ {{\rm{else}}{\rm{.}}} \\\end{array}$$
Let $A = 1\,{\rm V}$ and $T = 0.5\,{\rm ms}$ apply.
The Fourier transform of the triangular pulse $x(t)$ sketched above is assumed to be known, namely
- $$X( f ) = A \cdot T \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }}fT} ),$$
where $\text{si}(x) = \text{sin}(x)/x$.
A comparison of the two signals shows that the following relationship exists between the functions $x(t)$ and $y(t)$ :
- $$y(t) = T \cdot \frac{{{\rm d}x(t)}}{{{\rm d}t}}.$$
Hints:
- This task belongs to the chapter Fourier Transform Theorems.
- All the laws presented here - including the Shifting Theorem and the Differentiation Theorem – are illustrated with examples in the (German language) learning video
Gesetzmäßigkeiten der Fouriertransformation ⇒ "Regularities to the Fourier transform". - In subtask (3) the spectrum $Y(f)$ is to be calculated starting from a symmetrical rectangular pulse $r(t)$ with amplitude $A$ and duration $T$ and its spectrum $R(f) = A \cdot T \cdot \text{si}(\pi fT)$ . This is achieved by applying the Shifting Theorem.
- In Exercise 3.5Z the spectrum $Y(f)$ is calculated starting from a signal consisting of three Dirac functions by applying the Integration Theorem.
Questions
Solution
(1) The differentiation theorem reads generally:
- $$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm{j}} 2{\rm{\pi }}f \cdot X( f ).$$
- Applied to the present example, one obtains:
- $$Y( f ) = T \cdot {\rm{j}}\cdot 2{\rm{\pi }}f \cdot A \cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{( {{\rm{\pi }}fT} )^2 }} = {\rm{j}} \cdot 2 \cdot A\cdot T \cdot \frac{{\sin ^2 ( {{\rm{\pi }}fT} )}}{{{\rm{\pi }}fT}}.$$
- This function is purely imaginary. At the frequency $f = 0$ the imaginary part also disappears. This can be formally proven, for example, by applying l'Hospital's rule ⇒ $Y( f = 0 ) \;\underline{= 0}$.
- However, the result also follows from the fact that the spectral value at $f = 0$ is equal to the integral over the time function $y(t)$ .
- At the normalised frequency $f \cdot T = 0.5$ $($i.e for $f = 1\,\text{ kHz})$ the sine function is equal to $1$ and we obtain $|Y(f = 1 \,\text{kHz})| = 4/\pi \cdot A \cdot T$, i.e. approximately $|Y(f=1 \ \text{kHz})| \ \underline{=0.636 \,\text{ mV/Hz}}$ (positive imaginary).
(2) The correct solutions are 1 and 3:
- The zeros of $X(f)$ remain and there is another zero at the frequency $f = 0$.
- The upper bound is called the asymptotic curve
- $$\left| {Y_{\max }( f )} \right| = \frac{2A}{{{\rm{\pi }} \cdot |f|}} \ge \left| {Y( f )} \right|.$$
- For the frequencies at which the sine function delivers the values $\pm 1$ , $|Y_{\text{max}}(f)|$ and $|Y(f)|$ are identical.
- For the rectangular pulse of same amplitude $A$ the corresponding bound is $A/(\pi \cdot |f|)$.
- In contrast, the spectrum $X(f)$ of the triangular pulse falls asymptotically faster:
- $$\left| {X_{\max }( f )} \right| = \frac{A}{{{\rm{\pi }}^{\rm{2}} f^2 T}} \ge \left| {X( f )} \right|.$$
- This is due to the fact that $x(t)$ has no discontinuity points.
(3) Starting from a symmetrical rectangular pulse $r(t)$ with amplitude $A$ and duration $T$ the signal $y(t)$ can also be represented as follows:
- $$y(t) = r( {t + T/2} ) - r( {t - T/2} ).$$
- By applying the shifting theorem twice, one obtains:
- $$Y( f ) = R( f ) \cdot {\rm{e}}^{{\rm{j\pi }}fT} - R( f ) \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} .$$
- Using the relation $\text{e}^{\text{j}x} – \text{e}^{–\text{j}x} = 2\text{j} \cdot \text{sin}(x)$ it is also possible to write for this:
- $$Y( f ) = 2{\rm{j}} \cdot A \cdot T \cdot {\mathop{\rm si}\nolimits}( {{\rm{\pi }}fT} ) \cdot \sin ( {{\rm{\pi }}fT} ).$$
- Consequently, the result is the same as in subtask (1).
- Which way leads faster to the result, everyone must decide for himself. The author thinks that the first way is somewhat more favourable.
- Subjectively, we decide in favour of solution suggestion 1.