Difference between revisions of "Aufgaben:Exercise 4.3Z: Hilbert Transformator"
From LNTwww
m (Oezdemir moved page Aufgabe 4.3Z: Hilbert-Transformator to Exercise 4.3Z: Hilbert Transformator) |
|||
| (6 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID717__Sig_Z_4_3_neu.png|right|frame|Hilbert | + | [[File:P_ID717__Sig_Z_4_3_neu.png|right|frame|Hilbert transformator ]] |
| − | + | The diagram describes a model of how, at least mentally, | |
| − | * | + | *the analytical signal $x_{+}(t)$ can be generated, |
| − | * | + | *from the real band-pass signal $x(t)$. |
| − | + | ||
| − | + | The lower branch contains the so-called "Hilbert transformer" with the frequency response $H_{\rm HT}(f)$. | |
| − | + | Its output signal $y(t)$ is multiplied by the imaginary unit $\rm j$ and added to the signal $x(t)$ : | |
:$$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$ | :$$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$ | ||
| − | + | As test signals are used, each with $A = 1 \, \text{V}$ and $f_0 = 10 \, \text{kHz}$: | |
:$$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$ | :$$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$ | ||
:$$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$ | :$$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$ | ||
| − | :$$x_3(t) = A \cdot {\cos} \big( 2 \pi f_0 (t - \tau) \big) \hspace{0.3cm}{\rm | + | :$$x_3(t) = A \cdot {\cos} \big( 2 \pi f_0 (t - \tau) \big) \hspace{0.3cm}{\rm with}\hspace{0.3cm}\tau = 12.5 \hspace{0.1cm}{\rm µ s}.$$ |
| − | |||
| Line 23: | Line 22: | ||
| − | + | ''Hints:'' | |
| − | + | *This exercise belongs to the chapter [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function|Analytical Signal and its Spectral Function]]. | |
| − | '' | ||
| − | * | ||
| − | * | + | *The following applies to the spectral function of the analytical signal: |
:$$ X_{\rm +}(f)= \big[1 + {\rm sign}(f)\big] \cdot X(f).$$ | :$$ X_{\rm +}(f)= \big[1 + {\rm sign}(f)\big] \cdot X(f).$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the frequency response $H_{\rm HT}(f)$ of the Hilbert transformer. Which value is valid for the frequency $f_0 = 10 \text{ kHz}$? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[H_{\rm HT}(f = f_0)]\ = \ $ { 0. } | $\text{Re}[H_{\rm HT}(f = f_0)]\ = \ $ { 0. } | ||
| Line 41: | Line 38: | ||
| − | { | + | {What is the Hilbert transform $y_1(t)$ for the input signal $x_1(t)$? In particular, what value results at $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y_1(t = 0)\ = \ $ { 0. } $\rm V$ | $y_1(t = 0)\ = \ $ { 0. } $\rm V$ | ||
| − | { | + | {What is the Hilbert transform $y_2(t)$ for the input signal $x_2(t)$? Which value results in particular at $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y_2(t = 0)\ = \ $ { -1.03--0.97 } $\rm V$ | $y_2(t = 0)\ = \ $ { -1.03--0.97 } $\rm V$ | ||
| − | { | + | {What is the Hilbert transform $y_3(t)$ for the input signal $x_3(t)$? What value results for $t=0$? What is the phase delay $\varphi_{\rm HT}$ of the Hilbert transformer? |
|type="{}"} | |type="{}"} | ||
$\varphi_{\rm HT}\ = \ $ { 90 3% } $\text{Grad}$ | $\varphi_{\rm HT}\ = \ $ { 90 3% } $\text{Grad}$ | ||
| Line 57: | Line 54: | ||
| − | { | + | {What is the analytical signal associated with $x_3(t)$? What are the values of the real and imaginary parts of this complex signal at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[x_{3+}(t = 0)]\ = \ $ { 0.707 3% } $\text{V}$ | $\text{Re}[x_{3+}(t = 0)]\ = \ $ { 0.707 3% } $\text{V}$ | ||
| Line 66: | Line 63: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the spectral function at the model output holds: |
:$$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot | :$$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot | ||
X(f).$$ | X(f).$$ | ||
| − | * | + | *A comparison with the given relation |
:$$X_{\rm +}(f)= \left(1 + {\rm | :$$X_{\rm +}(f)= \left(1 + {\rm | ||
sign}(f)\right) \cdot X(f)$$ | sign}(f)\right) \cdot X(f)$$ | ||
| − | : | + | :shows that $H_{\rm HT}(f) = - {\rm j} \cdot \sign(f)$. |
| − | * | + | *Thus, the real part we are looking for is ${\rm Re}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=0}$ and the imaginary part is equal to ${\rm Im}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=-1}$. |
| − | '''(2)''' | + | '''(2)''' From the spectral function |
:$$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ | :$$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ | ||
{A}/{2}\cdot\delta (f - f_{0}).$$ | {A}/{2}\cdot\delta (f - f_{0}).$$ | ||
| − | : | + | :becomes according to the Hilbert transformer: |
:$$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | :$$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | ||
j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$ | j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$ | ||
| − | * | + | *Thus the signal at the output of the Hilbert transformer is: |
:$$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$ | :$$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$ | ||
| − | '''(3)''' | + | '''(3)''' Now the spectral functions at the input and output of the Hilbert transformer are: |
:$$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | :$$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | ||
j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$ | j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$ | ||
:$$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- | :$$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- | ||
{A}/{2}\cdot\delta (f - f_{0}).$$ | {A}/{2}\cdot\delta (f - f_{0}).$$ | ||
| − | * | + | *It follows that $y_2(t) = - A \cdot \cos(2\pi f_0 t)$ and $y_2(t = 0)\; \underline{= -\hspace{-0.08cm}1 \,\text{V}}$. |
| − | '''(4)''' | + | '''(4)''' This input signal can also be represented as follows: |
:$$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - | :$$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - | ||
2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = | 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = | ||
A \cdot {\cos} ( 2 \pi f_0 t - \pi/4)\hspace{0.3cm} | A \cdot {\cos} ( 2 \pi f_0 t - \pi/4)\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}y_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 3\pi/4).$$ | \Rightarrow \hspace{0.3cm}y_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 3\pi/4).$$ | ||
| − | * | + | *The signal phase is thus $\varphi = \pi /4$. |
| − | * | + | *The Hilbert transformer delays this by $\varphi_{\rm HT} \; \underline{= 90^\circ} \; (\pi /2)$. |
| − | * | + | *Therefore, the output signal $y_3(t) = A \cdot \cos(2\pi f_0 t -3 \pi /4)$ and the signal value at time $t = 0$ is $A \cdot \cos(135^\circ) \; \underline{= -0.707 \,\text{V}}$. |
| − | '''(5)''' | + | '''(5)''' The spectral function of the signal $x_3(t)$ is: |
:$$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta | :$$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta | ||
(f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} | (f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} | ||
\varphi}\cdot\delta (f - f_{\rm 0}) .$$ | \varphi}\cdot\delta (f - f_{\rm 0}) .$$ | ||
| − | * | + | *For the analytical signal, the first component disappears and the component at $+f_0$ is doubled: |
| + | |||
:$$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f | :$$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f | ||
- f_{\rm 0}) .$$ | - f_{\rm 0}) .$$ | ||
| − | * | + | *By applying the "Shifting Theorem" , the associated time function with $\varphi = \pi /4$ is: |
:$$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | :$$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | ||
\hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | ||
| − | * | + | *Specifically, for time $t = 0$: |
:$$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} | :$$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} | ||
\varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 | \varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 | ||
| Line 128: | Line 126: | ||
j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$ | j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$ | ||
| − | '' | + | |
| − | * | + | ''Hint'': |
| − | * | + | *To get from $x(t)$ to $x_+(t)$, just replace the cosine function with the complex exponential function. |
| + | *For example, the following applies to a harmonic oscillation: | ||
:$$x(t) = A \cdot {\cos} ( 2 \pi f_0 t | :$$x(t) = A \cdot {\cos} ( 2 \pi f_0 t | ||
-\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | -\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | ||
| Line 138: | Line 137: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^4.2 Analytical Signal and its Spectral Function^]] |
Latest revision as of 15:13, 24 May 2021
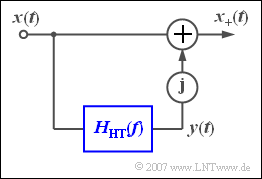
The diagram describes a model of how, at least mentally,
- the analytical signal $x_{+}(t)$ can be generated,
- from the real band-pass signal $x(t)$.
The lower branch contains the so-called "Hilbert transformer" with the frequency response $H_{\rm HT}(f)$.
Its output signal $y(t)$ is multiplied by the imaginary unit $\rm j$ and added to the signal $x(t)$ :
- $$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$
As test signals are used, each with $A = 1 \, \text{V}$ and $f_0 = 10 \, \text{kHz}$:
- $$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$
- $$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$
- $$x_3(t) = A \cdot {\cos} \big( 2 \pi f_0 (t - \tau) \big) \hspace{0.3cm}{\rm with}\hspace{0.3cm}\tau = 12.5 \hspace{0.1cm}{\rm µ s}.$$
Hints:
- This exercise belongs to the chapter Analytical Signal and its Spectral Function.
- The following applies to the spectral function of the analytical signal:
- $$ X_{\rm +}(f)= \big[1 + {\rm sign}(f)\big] \cdot X(f).$$
Questions
Solution
(1) For the spectral function at the model output holds:
- $$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot X(f).$$
- A comparison with the given relation
- $$X_{\rm +}(f)= \left(1 + {\rm sign}(f)\right) \cdot X(f)$$
- shows that $H_{\rm HT}(f) = - {\rm j} \cdot \sign(f)$.
- Thus, the real part we are looking for is ${\rm Re}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=0}$ and the imaginary part is equal to ${\rm Im}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=-1}$.
(2) From the spectral function
- $$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ {A}/{2}\cdot\delta (f - f_{0}).$$
- becomes according to the Hilbert transformer:
- $$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$
- Thus the signal at the output of the Hilbert transformer is:
- $$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$
(3) Now the spectral functions at the input and output of the Hilbert transformer are:
- $$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$
- $$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- {A}/{2}\cdot\delta (f - f_{0}).$$
- It follows that $y_2(t) = - A \cdot \cos(2\pi f_0 t)$ and $y_2(t = 0)\; \underline{= -\hspace{-0.08cm}1 \,\text{V}}$.
(4) This input signal can also be represented as follows:
- $$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = A \cdot {\cos} ( 2 \pi f_0 t - \pi/4)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 3\pi/4).$$
- The signal phase is thus $\varphi = \pi /4$.
- The Hilbert transformer delays this by $\varphi_{\rm HT} \; \underline{= 90^\circ} \; (\pi /2)$.
- Therefore, the output signal $y_3(t) = A \cdot \cos(2\pi f_0 t -3 \pi /4)$ and the signal value at time $t = 0$ is $A \cdot \cos(135^\circ) \; \underline{= -0.707 \,\text{V}}$.
(5) The spectral function of the signal $x_3(t)$ is:
- $$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta (f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm 0}) .$$
- For the analytical signal, the first component disappears and the component at $+f_0$ is doubled:
- $$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm 0}) .$$
- By applying the "Shifting Theorem" , the associated time function with $\varphi = \pi /4$ is:
- $$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
- Specifically, for time $t = 0$:
- $$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 \cdot{\sin} ( 45^\circ)= \hspace{0.15 cm}\underline{{\rm 0.707 \hspace{0.05cm} V}-{\rm j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$
Hint:
- To get from $x(t)$ to $x_+(t)$, just replace the cosine function with the complex exponential function.
- For example, the following applies to a harmonic oscillation:
- $$x(t) = A \cdot {\cos} ( 2 \pi f_0 t -\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$