Difference between revisions of "Applets:Graphical Convolution"
(Created page with "{{LntAppletLink|convolution}} == Applet Description== <br> Dieses Applet verdeutlicht die Faltungsoperation im Zeitbereich *zwischen einem Eingangsimpuls $x(t)$  ...") |
|||
| (22 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLinkEnDe|convolution_en|convolution}} |
== Applet Description== | == Applet Description== | ||
<br> | <br> | ||
| − | + | This applet illustrates the convolution operation in the time domain | |
| − | * | + | *between an input pulse $x(t)$ ⇒ rectangle, triangle, Gaussian, exponential function |
| − | * | + | *and the impulse response $h(t)$ of an LTI system with low–pass character ⇒ slit low–pass, first or second order low–pass, Gaussian low–pass. |
| − | + | For the output signal $y(t)$ corresponding to the block diagram in $\text{Example 1}$, then, as stated in the chapter [[Applets:Graphical_Convolution#Graphical_Convolution|"Graphical Convolution"]]: | |
:$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau .$$ | :$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau .$$ | ||
| − | + | For causal systems ⇒ $h(t) \equiv 0$ for $t < 0$ (examples: slit low–pass as well as first and second order low–pass) can be written for this also: | |
:$$y( t ) = \int_{ - \infty }^{ t } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau .$$ | :$$y( t ) = \int_{ - \infty }^{ t } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau .$$ | ||
| − | + | Please note: | |
| − | * | + | *All quantities – also the time $t$ – are to be understood normalized (dimensionless). |
| − | * | + | *The time functions $x(t)$, $h(t)$ and $y(t)$ cannot assume negative signal values in the program. |
| − | * | + | *The ''absolute duration'' of a pulse $y(t)$ is the (continuous) time range for which $y(t) > 0$. |
| − | * | + | *The ''equivalent duration'' of a pulse can be calculated by the rectangle of equal area. |
==Theoretical Background== | ==Theoretical Background== | ||
| − | === | + | ===Convolution in the time domain=== |
| − | + | The [[Signal_Representation/The_Convolution_Theorem_and_Operation|"convolution theorem"]] is one of the most important laws of the Fourier transform. We first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known: | |
:$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ | :$$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$ | ||
| − | + | Then for the time function of the product $X_1(f) \cdot X_2(f)$ holds: | |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | Here $\tau$ is a formal integration variable with the dimension of a time. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The above connection of the time function $x_1(t)$ and $x_2(t)$ is called '''convolution''' and represents this functional connection with a star: |
:$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | Thus, above Fourier correspondence can also be written as follows: | |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$ | ||
| − | [[Signal_Representation/The_Convolution_Theorem_and_Operation# | + | [[Signal_Representation/The_Convolution_Theorem_and_Operation#Proof_of_the_Convolution_Theorem|$\text{"Proof"}$]]}} |
| − | '' | + | ''Note'': The convolution is '''commutative''' ⇒ The order of the operands is interchangeable: ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t ) $. |
| − | [[File: | + | [[File:EN_Sig_T_3_4_S1.png|right|frame|For the calculation of signal and spectrum at the LTI output]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ Any linear time-invariant (LTI) system can be described both by the frequency response $H(f)$ and by the impulse response $h(t)$, the relationship between these two system quantities also being given by the Fourier transform. |
| − | + | If a signal $x(t)$ with the spectrum $X(f)$ is applied to the input, the following applies to the spectrum of the output signal: | |
:$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | :$$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$ | ||
| − | + | With the convolution theorem it is now possible to calculate the output signal also directly in the time domain: | |
:$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ | :$$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$ | ||
| − | + | From this equation, it is again clear that the convolution operation is ''commutative''. }} | |
| − | === | + | ===Convolution in the frequency domain=== |
| − | + | The duality between the time and frequency domains also allows us to make statements regarding the spectrum of a product signal: | |
:$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | :$$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$ | ||
| − | + | This result can be proved similarly to the [[Applets:Graphical_Convolution#Convolution_in_the_time_domain|"convolution theorem in the time domain"]]. However, the integration variable $\nu$ now has the dimension of a frequency. | |
| − | [[File: | + | [[File:EN_Sig_T_3_4_S2.png|right|frame|Convolution in the frequency domain]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The [[Modulation_Methods/Double-Sideband_Amplitude_Modulation#Description_in_the_time_domain|"double-sideband amplitude modulation"]] (DSB-AM) without carrier is described by the sketched model. |
| − | * | + | *In the time domain representation (blue), the modulated signal $s(t)$ is the product of the message signal $q(t)$ and the (normalized) carrier signal $z(t)$. |
| − | * | + | *According to the convolution theorem, it follows for the frequency domain (red) that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)$ and $Z(f)$. }} |
| − | === | + | ===Convolution of a function with a Dirac delta function=== |
| − | + | The convolution operation becomes very simple if one of the two operands is a [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Dirac_.28delta.29_function_in_frequency_domain|"Dirac delta function"]]. This is equally true for convolution in the time and frequency domain. | |
| − | + | As an example, we consider the convolution of a function $x_1(t)$ with the function | |
:$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T}.$$ | :$$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T}.$$ | ||
| − | + | Then for the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ holds: | |
:$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T} .$$ | :$$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T} .$$ | ||
| − | + | The complex exponential function leads to a shift by $T$ ⇒ [[Signal_Representation/Fourier_Transform_Theorems#Shifting_Theorem|"shifting theorem"]], the factor $\alpha$ to an attenuation $(\alpha < 1)$ or an amplification $(\alpha > 1)$. It follows that: | |
:$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | :$$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{In | + | $\text{In words: }$ The convolution of an arbitrary function with a Dirac delta function at $t = T$ results in the function shifted to the right by $T$, whereby the weighting of the Dirac delta function by the factor $\alpha$ must still be taken into account.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ A rectangular signal $x(t)$ is delayed by a running time $\tau = 3\,\text{ ms}$ and attenuated by a factor $\alpha = 0.5$ by an LTI system. |
| − | [[File:P_ID522__Sig_T_3_4_S3_neu.png|center|frame| | + | [[File:P_ID522__Sig_T_3_4_S3_neu.png|center|frame|Convolution of a rectangle with a Dirac delta function]] |
| − | + | Shift and attenuation can be seen in the output signal $y(t)$ as well as in the impulse response $h(t)$.}} | |
| − | === | + | ===Graphical Convolution=== |
| − | + | This applet assumes the following convolution operation: | |
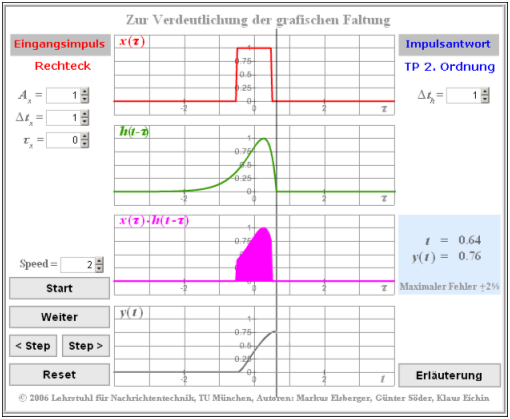
| − | [[File:P_ID2723__Sig_T_3_4_programm.png|right|frame| | + | [[File:P_ID2723__Sig_T_3_4_programm.png|right|frame|Screen capture of the program "Graphical Convolution" (former version)]] |
:$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | The solution of the convolution integral is to be done graphically. It is assumed that $x(t)$ and $h(t)$ are continuous-time signals. | |
| − | + | Then the following steps are required: | |
| − | # | + | # '''Change''' the '''time variables''' of the two functions: <br> $x(t) \to x(\tau)$, $h(t) \to h(\tau)$. |
| − | # | + | # '''Mirror''' second '''function''': $h(\tau) \to h(-\tau)$. |
| − | # | + | # '''Shift''' mirrored '''function''' by $t$: $h(-\tau) \to h(t-\tau)$. |
| − | # ''' | + | # '''Multiplication''' of the two functions $x(\tau)$ and $h(t-\tau)$. |
| − | # '''Integration''' | + | # '''Integration''' over the product with respect to $\tau$ in the limits from $-\infty$ to $+\infty$. |
| − | + | Since the convolution is commutative, $h(\tau)$ can be mirrored instead of $x(\tau)$. | |
<br><br> | <br><br> | ||
| − | + | The accompanying graphic shows a screen shot of an older version of this applet. | |
<br><br> | <br><br> | ||
| − | [[File:P_ID582__Sig_T_3_4_S4_neu.png|right|frame| | + | [[File:P_ID582__Sig_T_3_4_S4_neu.png|right|frame|Example of a convolution operation: <br>Jump function convolved with exponential function]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
| − | + | The procedure of graphical convolution is now explained with a detailed example: | |
| − | * | + | *Let a jump function $x(t) = \gamma(t)$ be applied to the input of a filter. |
| − | * | + | *Let the impulse response of the RC low-pass filter be $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$ |
| − | + | The graph shows the input signal $x(\tau)$ in red, the impulse response $h(\tau)$ in blue, and the output signal $y(\tau)$ in gray. | |
| − | + | The time axis has already been renamed $\tau$. | |
| − | + | The output signal can be calculated, for example, according to the following equation: | |
:$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | A few more remarks on the graphical convolution: | |
| − | * | + | *The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$, multiplying this mirrored signal $x(-\tau)$ by the impulse response $h(\tau)$, and integrating over it. |
| − | * | + | *Since there is no time interval here where both the blue curve $h(\tau)$ and at the same time the red dashed mirroring $x(-\tau)$ is not equal to zero, it follows that $y(t=0)=0$. |
| − | * | + | *For any other time $t$, the input signal must be shifted ⇒ $x(t-\tau)$, for example corresponding to the green dashed curve for $t=T$. |
| − | * | + | *Since in this example also $x(t-\tau)$ can only take the values $0$ or $1$, the integration $($generally from $\tau_1$ to $\tau_2)$ becomes simple and we obtain with $\tau_1 = 0$ and $\tau_2 = t$ : |
:$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | :$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | ||
| − | + | The sketch is valid for $t=T$ and leads to the initial value $y(t=T) = 1 – 1/\text{e} \approx 0.632$.}} | |
==Exercises== | ==Exercises== | ||
| − | *First, select the number $(1,\ 2, \text{...} \ )$ of the | + | *First, select the number $(1,\ 2, \text{...} \ )$ of the exercise to be processed. The number $0$ corresponds to a "Reset": Same setting as at program start. |
| − | * | + | * An exercise description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution". |
| + | *Both the input signal $x(t)$ and the impulse response $h(t)$ of the filter are are normalized, dimensionless and energy-limited ("time-limited pulses"). | ||
| − | |||
| − | |||
| − | |||
| − | + | {{BlueBox|TEXT= | |
| − | + | '''(1)''' Select the following parameters: $\text{Gaussian pulse: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 1; \text{ Impulse response according to 2nd order low-pass: } \Delta t_h= 1$. | |
| + | <br> Interpret the displayed graphs. What is the maximum output value $y_{\rm max}$? At what time $t_{\rm max}$ does $y_{\rm max}$ occur? }} | ||
| − | : | + | * After renaming: Input signal $x(\tau)$ ⇒ red curve, impulse response $h(\tau)$ ⇒ blue curve, after mirroring $h(-\tau)$ ⇒ green curve. |
| − | + | * Shifting the green curve by $t$ to the right, we get $h(t-\tau)$. The output signal $y(t)$ is obtained by multiplication and integration with respect to $\tau$: | |
| − | {{ | + | :$$y (t) = \int_{ - \infty }^{ +\infty } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ t } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau .$$ |
| − | + | * The output pulse $y(t)$ is asymmetric in the present case; the maximum output value $y_{\rm max}\approx 0.67$ occurs at $t_{\rm max}\approx 1.5$. | |
| − | |||
| − | |||
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''( | + | '''(2)''' What changes if we increase the equivalent pulse duration of $h(t)$ to $\Delta t_h= 1.5$? }} |
| − | |||
| − | + | * $y_{\rm max}\approx 0.53$ now occurs at $t_{\rm max}\approx 1.75$. Due to the less favorable (wider) impulse response, the input pulse is more deformed. | |
| − | + | * In a digital communication system, this would result in stronger "intersymbol interferences". | |
| − | |||
| − | |||
| − | |||
| − | + | {{BlueBox|TEXT= | |
| − | + | '''(3)''' Now select the symmetric $\text{rectangular pulse: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ and the $\text{rectangular impulse response}$ of the low-pass filter: $\Delta t_h= 1$. | |
| + | <br> Interpret the convolution result. What is the maximum output value $y_{\rm max}$? At what times is $y(t)>0$? Does $h(t)$ describe a causal system? }} | ||
| − | + | * The convolution of two rectangles with respective durations $1$ yields a triangle with absolute duration $2$ ⇒ equivalent pulse duration $\Delta t_y= 1$. | |
| − | + | * $y(t)$ is different from zero in the range from $-0.5$ to $+1.5$ . The pulse maximum $y_{\rm max} = 1$ is at $t_{\rm max} = +0.5$. | |
| − | + | * $h(t)$ describes a causal system, since $h(t) \equiv 0$ for $t < 0$. That means: The "effect" $y(t)$ does not come before the "cause" $x(t)$. | |
| − | |||
| − | |||
| − | |||
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''( | + | '''(4)''' What changes if we increase the equivalent pulse duration of $h(t)$ to $\Delta t_h= 2$ ? }} |
| − | + | * The convolution of two rectangles of different widths results in a trapezoid, here between $-0.5$ and $+2.5$ ⇒ equivalent pulse duration $\Delta t_y= 2$. | |
| − | + | * The maximum $y_{\rm max} = 0.5$ occurs in the range $0.5 \le t \le 1.5$. Nothing changes with respect to causality. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{BlueBox|TEXT= | |
| − | + | '''(5)''' Now select the (unsymmetrical) $\text{rectangular pulse: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0.5$ and the $\text{impulse response of a 1st order low-pass: }\Delta t_h= 1$. | |
| − | + | <br> Interpret the results. What is the value of $y_{\rm max}$? At what times is $y(t)>0$ ? Does $h(t)$ describe a causal system? }} | |
| − | + | * $h(t)$ has an exponentially decreasing curve for $t > 0$. It always applies: $y(t>0) > 0$, but the signal values can become very small. | |
| − | + | * $y_{\rm max} = 0.63$ occurs for $t_{\rm max} = +1$. For $ t < t_{\rm max}$ the progression is exponentially increasing, for $ t > t_{\rm max}$ exponentially decreasing. | |
| − | + | * The 1st order low-pass can be realized with a resistor and a capacitor. Any realizable system is causal per se. | |
| − | |||
| − | |||
| − | {{ | + | {{BlueBox|TEXT= |
| − | '''( | + | '''(6)''' Select as in $(3)$ the $\text{rectangular impulse response}$ of the low-pass filter: $\Delta t_h= 1$. With which $x(t)$ results the same $y(t)$ as for $(5)$?}} |
| − | |||
| − | + | * The signal $y(t)$ in $(5)$ resulted as a convolution between the rectangular input $x(t)$ and the exponential function $h(t)$. | |
| − | + | * Since the convolution operation is commutative, the same result is obtained with the exponential function $x(t)$ and the rectangular function $h(t)$. | |
| + | * Thus, the correct setting for the input signal $x(t)$ is the $\text{exponential pulse }$with $ A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ . | ||
| + | |||
| + | |||
| + | {{BlueBox|TEXT= | ||
| + | '''(7)''' For the remainder of the exercises, we consider the Gaussian low-pass. The equivalent duration of the impulse response $h(t)$ should first be $\Delta t_h= 0.8$. | ||
| + | <br> Analyze and interpret this "system" in terms of causality and the resulting distortions for the rectangular pulse. }} | ||
| + | |||
| + | * The low-pass is not causal (and therefore non–realizable): For $t < 0$: $h(t) \equiv 0$ does not hold. Suitable model if infinite delay is ignored. | ||
| + | * The larger $\Delta t_h$ is, the wider the output pulse and the stronger the degradation of a digital system due to intersymbol interference. | ||
| + | * The frequency response $H(f)$ is the Fourier transform of $h(t)$. The larger $\Delta t_h$ is, the smaller $\Delta f_h = 1/\Delta t_h$ ⇒ The system is more narrowband. | ||
| + | |||
| + | |||
| + | {{BlueBox|TEXT= | ||
| + | '''(8)''' Now select $\text{Gaussian pulse: }A_x = 1, \ \Delta t_x= 1.5, \ \tau_x = 0$ and $\text{Gaussian low-pass: }\Delta t_h= 2$. What is the course of the output pulse $y(t)$? | ||
| + | <br> What are the equivalent duration $\Delta t_y$ of the output pulse and the maximum output value $y_{\rm max}$? At what time $t_{\rm max}$ does $y_{\rm max}$ occur? }} | ||
| + | |||
| + | * $y(t)$ is (exactly) Gaussian, too. Mnemonic: $\text{"Gaussian convolved with Gaussian gives always Gaussian"}$. | ||
| + | * Equivalent duration: $\Delta t_y =\sqrt{\Delta t_x^2+ \Delta t_h^2} = 2.5$. Pulse maximum $($at $t=0)$: $y_{\rm max} = A_x \cdot \Delta t_x/\Delta t_y = 1 \cdot 1.5/2.5 = 0.6$. | ||
| + | |||
| + | |||
| + | {{BlueBox|TEXT= | ||
| + | '''(9)''' Now select $\text{Triangular pulse: }A_x = 1, \ \Delta t_x= 1.5, \ \tau_x = 0$ and $\text{Gaussian low–pass: }\Delta t_h= 2$. What is the course of the output pulse $y(t)$? | ||
| + | <br> What is the equivalent duration $\Delta t_y$ of the output pulse and the maximum output value $y_{\rm max}$? At what time $t_{\rm max}$ does $y_{\rm max}$ occur?}} | ||
| + | |||
| + | * $y(t)$ is nearly Gaussian, but not exactly. Mnemonic: $\text{"Gaussian convolved with non–Gaussian never gives exactly Gaussian"}$. | ||
| + | * The characteristics of the output pulse $y(t)$ differ only slightly from $(8)$: $\Delta t_y \approx 2.551$, $y_{\rm max} \approx 0.588$. | ||
| + | |||
| + | |||
==Applet Manual== | ==Applet Manual== | ||
<br> | <br> | ||
| − | [[File:Anleitung_Faltung_2.png|right]] | + | [[File:Anleitung_Faltung_2.png|right|frame|Screen shot (German version)]] |
| − | '''(A)''' | + | '''(A)''' Selection: Shape of the input pulse $x(t)$ |
| − | '''(B)''' | + | '''(B)''' Parameter input for the input pulse $x(t)$ |
| − | '''(C)''' | + | '''(C)''' Selection: Shape of the impulse response $h(t)$ of the low-pass system |
| − | '''(D)''' | + | '''(D)''' Parameter input for the impulse response $h(t)$ |
| − | '''(E)''' | + | '''(E)''' Control panel (Start; Pause/Continue ; Step > ; Step < ; Reset) |
| − | '''(F)''' | + | '''(F)''' Output the initial value $y(t)$ at the continuous time $t$ |
| − | '''(G)''' | + | '''(G)''' Maximum value $y_{\rm max} = y(t_{\rm max})$ and equivalent width $\Delta\hspace{0.03cm} t_y$ |
| − | | + | After renaming the abscissa: $t \ \to \ \tau$: |
| − | '''(H)''' | + | '''(H)''' Representation of $x(\tau)$ ⇒ red static curve. |
| − | '''(I)''' | + | '''(I)''' Representation of $h(\tau)$ ⇒ blue curve and $h(t-\tau)$ ⇒ green curve<br> $($this is shifted to the right with the motion parameter $t$ $)$ |
| − | '''(J)''' | + | '''(J)''' Plot of $x(\tau) \cdot h(t - \tau)$ ⇒ purple curve, dynamic with $t$ |
| − | '''(K)''' | + | '''(K)''' Successive representation of the output signal $y(t)$ ⇒ brown curve |
| − | '''(L)''' | + | '''(L)''' Area for exercise execution: Exercise selection. |
| − | '''(M)''' | + | '''(M)''' Exercise execution: Area for exercise description |
| − | '''(N)''' | + | '''(N)''' Exercise execution: Area for the sample solution |
<br clear=all> | <br clear=all> | ||
==About the Authors== | ==About the Authors== | ||
| − | + | This interactive calculation tool was designed and implemented at the [https://www.ei.tum.de/en/lnt/home/ Institute for Communications Engineering] at the [https://www.tum.de/en Technical University of Munich]. | |
| − | * | + | *The first version was created in 2006 by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Markus_Elsberger_.28Diplomarbeit_LB_2006.29|Markus Elsberger]] as part of his bachelor thesis with “FlashMX – Actionscript” (Supervisor: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | * | + | |
| + | *Last revision and English version 2020/2021 by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] in the context of a working student activity. | ||
| + | |||
| + | |||
| + | The conversion of this applet to HTML 5 was financially supported by [https://www.ei.tum.de/studium/studienzuschuesse/ Studienzuschüsse] ("study grants") of the TUM Faculty EI. Many thanks. | ||
| − | |||
==Once again: Open Applet in new Tab== | ==Once again: Open Applet in new Tab== | ||
| − | + | {{LntAppletLinkEnDe|convolution_en|convolution}} | |
| − | {{ | ||
Latest revision as of 16:30, 10 April 2023
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
This applet illustrates the convolution operation in the time domain
- between an input pulse $x(t)$ ⇒ rectangle, triangle, Gaussian, exponential function
- and the impulse response $h(t)$ of an LTI system with low–pass character ⇒ slit low–pass, first or second order low–pass, Gaussian low–pass.
For the output signal $y(t)$ corresponding to the block diagram in $\text{Example 1}$, then, as stated in the chapter "Graphical Convolution":
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau .$$
For causal systems ⇒ $h(t) \equiv 0$ for $t < 0$ (examples: slit low–pass as well as first and second order low–pass) can be written for this also:
- $$y( t ) = \int_{ - \infty }^{ t } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau .$$
Please note:
- All quantities – also the time $t$ – are to be understood normalized (dimensionless).
- The time functions $x(t)$, $h(t)$ and $y(t)$ cannot assume negative signal values in the program.
- The absolute duration of a pulse $y(t)$ is the (continuous) time range for which $y(t) > 0$.
- The equivalent duration of a pulse can be calculated by the rectangle of equal area.
Theoretical Background
Convolution in the time domain
The "convolution theorem" is one of the most important laws of the Fourier transform. We first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known:
- $$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$
Then for the time function of the product $X_1(f) \cdot X_2(f)$ holds:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Here $\tau$ is a formal integration variable with the dimension of a time.
$\text{Definition:}$ The above connection of the time function $x_1(t)$ and $x_2(t)$ is called convolution and represents this functional connection with a star:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
Thus, above Fourier correspondence can also be written as follows:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
Note: The convolution is commutative ⇒ The order of the operands is interchangeable: ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t ) $.
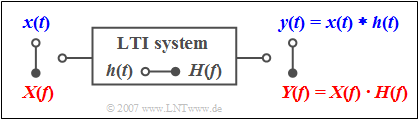
$\text{Example 1:}$ Any linear time-invariant (LTI) system can be described both by the frequency response $H(f)$ and by the impulse response $h(t)$, the relationship between these two system quantities also being given by the Fourier transform.
If a signal $x(t)$ with the spectrum $X(f)$ is applied to the input, the following applies to the spectrum of the output signal:
- $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$
With the convolution theorem it is now possible to calculate the output signal also directly in the time domain:
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$
From this equation, it is again clear that the convolution operation is commutative.
Convolution in the frequency domain
The duality between the time and frequency domains also allows us to make statements regarding the spectrum of a product signal:
- $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$
This result can be proved similarly to the "convolution theorem in the time domain". However, the integration variable $\nu$ now has the dimension of a frequency.
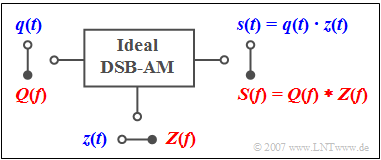
$\text{Example 2:}$ The "double-sideband amplitude modulation" (DSB-AM) without carrier is described by the sketched model.
- In the time domain representation (blue), the modulated signal $s(t)$ is the product of the message signal $q(t)$ and the (normalized) carrier signal $z(t)$.
- According to the convolution theorem, it follows for the frequency domain (red) that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)$ and $Z(f)$.
Convolution of a function with a Dirac delta function
The convolution operation becomes very simple if one of the two operands is a "Dirac delta function". This is equally true for convolution in the time and frequency domain.
As an example, we consider the convolution of a function $x_1(t)$ with the function
- $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T}.$$
Then for the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ holds:
- $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.03cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.01cm}f\hspace{0.01cm}T} .$$
The complex exponential function leads to a shift by $T$ ⇒ "shifting theorem", the factor $\alpha$ to an attenuation $(\alpha < 1)$ or an amplification $(\alpha > 1)$. It follows that:
- $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$
$\text{In words: }$ The convolution of an arbitrary function with a Dirac delta function at $t = T$ results in the function shifted to the right by $T$, whereby the weighting of the Dirac delta function by the factor $\alpha$ must still be taken into account.
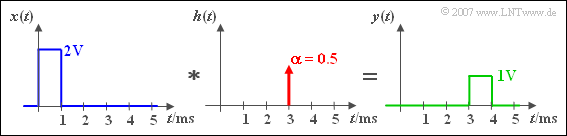
$\text{Example 3:}$ A rectangular signal $x(t)$ is delayed by a running time $\tau = 3\,\text{ ms}$ and attenuated by a factor $\alpha = 0.5$ by an LTI system.
Shift and attenuation can be seen in the output signal $y(t)$ as well as in the impulse response $h(t)$.
Graphical Convolution
This applet assumes the following convolution operation:
- $$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
The solution of the convolution integral is to be done graphically. It is assumed that $x(t)$ and $h(t)$ are continuous-time signals.
Then the following steps are required:
- Change the time variables of the two functions:
$x(t) \to x(\tau)$, $h(t) \to h(\tau)$. - Mirror second function: $h(\tau) \to h(-\tau)$.
- Shift mirrored function by $t$: $h(-\tau) \to h(t-\tau)$.
- Multiplication of the two functions $x(\tau)$ and $h(t-\tau)$.
- Integration over the product with respect to $\tau$ in the limits from $-\infty$ to $+\infty$.
Since the convolution is commutative, $h(\tau)$ can be mirrored instead of $x(\tau)$.
The accompanying graphic shows a screen shot of an older version of this applet.
$\text{Example 4:}$ The procedure of graphical convolution is now explained with a detailed example:
- Let a jump function $x(t) = \gamma(t)$ be applied to the input of a filter.
- Let the impulse response of the RC low-pass filter be $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/T}.$
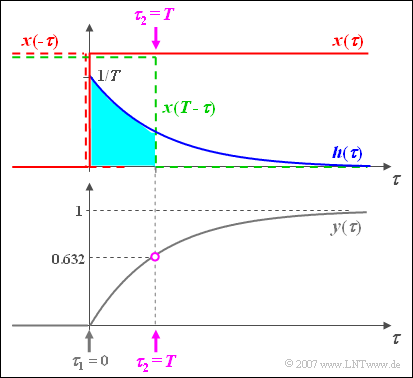
The graph shows the input signal $x(\tau)$ in red, the impulse response $h(\tau)$ in blue, and the output signal $y(\tau)$ in gray.
The time axis has already been renamed $\tau$.
The output signal can be calculated, for example, according to the following equation:
- $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
A few more remarks on the graphical convolution:
- The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$, multiplying this mirrored signal $x(-\tau)$ by the impulse response $h(\tau)$, and integrating over it.
- Since there is no time interval here where both the blue curve $h(\tau)$ and at the same time the red dashed mirroring $x(-\tau)$ is not equal to zero, it follows that $y(t=0)=0$.
- For any other time $t$, the input signal must be shifted ⇒ $x(t-\tau)$, for example corresponding to the green dashed curve for $t=T$.
- Since in this example also $x(t-\tau)$ can only take the values $0$ or $1$, the integration $($generally from $\tau_1$ to $\tau_2)$ becomes simple and we obtain with $\tau_1 = 0$ and $\tau_2 = t$ :
- $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$
The sketch is valid for $t=T$ and leads to the initial value $y(t=T) = 1 – 1/\text{e} \approx 0.632$.
Exercises
- First, select the number $(1,\ 2, \text{...} \ )$ of the exercise to be processed. The number $0$ corresponds to a "Reset": Same setting as at program start.
- An exercise description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution".
- Both the input signal $x(t)$ and the impulse response $h(t)$ of the filter are are normalized, dimensionless and energy-limited ("time-limited pulses").
(1) Select the following parameters: $\text{Gaussian pulse: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 1; \text{ Impulse response according to 2nd order low-pass: } \Delta t_h= 1$.
Interpret the displayed graphs. What is the maximum output value $y_{\rm max}$? At what time $t_{\rm max}$ does $y_{\rm max}$ occur?
- After renaming: Input signal $x(\tau)$ ⇒ red curve, impulse response $h(\tau)$ ⇒ blue curve, after mirroring $h(-\tau)$ ⇒ green curve.
- Shifting the green curve by $t$ to the right, we get $h(t-\tau)$. The output signal $y(t)$ is obtained by multiplication and integration with respect to $\tau$:
- $$y (t) = \int_{ - \infty }^{ +\infty } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ t } {x ( \tau ) } \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau .$$
- The output pulse $y(t)$ is asymmetric in the present case; the maximum output value $y_{\rm max}\approx 0.67$ occurs at $t_{\rm max}\approx 1.5$.
(2) What changes if we increase the equivalent pulse duration of $h(t)$ to $\Delta t_h= 1.5$?
- $y_{\rm max}\approx 0.53$ now occurs at $t_{\rm max}\approx 1.75$. Due to the less favorable (wider) impulse response, the input pulse is more deformed.
- In a digital communication system, this would result in stronger "intersymbol interferences".
(3) Now select the symmetric $\text{rectangular pulse: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ and the $\text{rectangular impulse response}$ of the low-pass filter: $\Delta t_h= 1$.
Interpret the convolution result. What is the maximum output value $y_{\rm max}$? At what times is $y(t)>0$? Does $h(t)$ describe a causal system?
- The convolution of two rectangles with respective durations $1$ yields a triangle with absolute duration $2$ ⇒ equivalent pulse duration $\Delta t_y= 1$.
- $y(t)$ is different from zero in the range from $-0.5$ to $+1.5$ . The pulse maximum $y_{\rm max} = 1$ is at $t_{\rm max} = +0.5$.
- $h(t)$ describes a causal system, since $h(t) \equiv 0$ for $t < 0$. That means: The "effect" $y(t)$ does not come before the "cause" $x(t)$.
(4) What changes if we increase the equivalent pulse duration of $h(t)$ to $\Delta t_h= 2$ ?
- The convolution of two rectangles of different widths results in a trapezoid, here between $-0.5$ and $+2.5$ ⇒ equivalent pulse duration $\Delta t_y= 2$.
- The maximum $y_{\rm max} = 0.5$ occurs in the range $0.5 \le t \le 1.5$. Nothing changes with respect to causality.
(5) Now select the (unsymmetrical) $\text{rectangular pulse: }A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0.5$ and the $\text{impulse response of a 1st order low-pass: }\Delta t_h= 1$.
Interpret the results. What is the value of $y_{\rm max}$? At what times is $y(t)>0$ ? Does $h(t)$ describe a causal system?
- $h(t)$ has an exponentially decreasing curve for $t > 0$. It always applies: $y(t>0) > 0$, but the signal values can become very small.
- $y_{\rm max} = 0.63$ occurs for $t_{\rm max} = +1$. For $ t < t_{\rm max}$ the progression is exponentially increasing, for $ t > t_{\rm max}$ exponentially decreasing.
- The 1st order low-pass can be realized with a resistor and a capacitor. Any realizable system is causal per se.
(6) Select as in $(3)$ the $\text{rectangular impulse response}$ of the low-pass filter: $\Delta t_h= 1$. With which $x(t)$ results the same $y(t)$ as for $(5)$?
- The signal $y(t)$ in $(5)$ resulted as a convolution between the rectangular input $x(t)$ and the exponential function $h(t)$.
- Since the convolution operation is commutative, the same result is obtained with the exponential function $x(t)$ and the rectangular function $h(t)$.
- Thus, the correct setting for the input signal $x(t)$ is the $\text{exponential pulse }$with $ A_x = 1, \ \Delta t_x= 1, \ \tau_x = 0$ .
(7) For the remainder of the exercises, we consider the Gaussian low-pass. The equivalent duration of the impulse response $h(t)$ should first be $\Delta t_h= 0.8$.
Analyze and interpret this "system" in terms of causality and the resulting distortions for the rectangular pulse.
- The low-pass is not causal (and therefore non–realizable): For $t < 0$: $h(t) \equiv 0$ does not hold. Suitable model if infinite delay is ignored.
- The larger $\Delta t_h$ is, the wider the output pulse and the stronger the degradation of a digital system due to intersymbol interference.
- The frequency response $H(f)$ is the Fourier transform of $h(t)$. The larger $\Delta t_h$ is, the smaller $\Delta f_h = 1/\Delta t_h$ ⇒ The system is more narrowband.
(8) Now select $\text{Gaussian pulse: }A_x = 1, \ \Delta t_x= 1.5, \ \tau_x = 0$ and $\text{Gaussian low-pass: }\Delta t_h= 2$. What is the course of the output pulse $y(t)$?
What are the equivalent duration $\Delta t_y$ of the output pulse and the maximum output value $y_{\rm max}$? At what time $t_{\rm max}$ does $y_{\rm max}$ occur?
- $y(t)$ is (exactly) Gaussian, too. Mnemonic: $\text{"Gaussian convolved with Gaussian gives always Gaussian"}$.
- Equivalent duration: $\Delta t_y =\sqrt{\Delta t_x^2+ \Delta t_h^2} = 2.5$. Pulse maximum $($at $t=0)$: $y_{\rm max} = A_x \cdot \Delta t_x/\Delta t_y = 1 \cdot 1.5/2.5 = 0.6$.
(9) Now select $\text{Triangular pulse: }A_x = 1, \ \Delta t_x= 1.5, \ \tau_x = 0$ and $\text{Gaussian low–pass: }\Delta t_h= 2$. What is the course of the output pulse $y(t)$?
What is the equivalent duration $\Delta t_y$ of the output pulse and the maximum output value $y_{\rm max}$? At what time $t_{\rm max}$ does $y_{\rm max}$ occur?
- $y(t)$ is nearly Gaussian, but not exactly. Mnemonic: $\text{"Gaussian convolved with non–Gaussian never gives exactly Gaussian"}$.
- The characteristics of the output pulse $y(t)$ differ only slightly from $(8)$: $\Delta t_y \approx 2.551$, $y_{\rm max} \approx 0.588$.
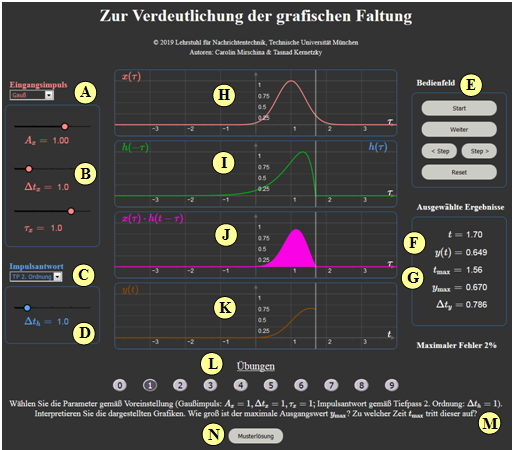
Applet Manual
(A) Selection: Shape of the input pulse $x(t)$
(B) Parameter input for the input pulse $x(t)$
(C) Selection: Shape of the impulse response $h(t)$ of the low-pass system
(D) Parameter input for the impulse response $h(t)$
(E) Control panel (Start; Pause/Continue ; Step > ; Step < ; Reset)
(F) Output the initial value $y(t)$ at the continuous time $t$
(G) Maximum value $y_{\rm max} = y(t_{\rm max})$ and equivalent width $\Delta\hspace{0.03cm} t_y$
After renaming the abscissa: $t \ \to \ \tau$:
(H) Representation of $x(\tau)$ ⇒ red static curve.
(I) Representation of $h(\tau)$ ⇒ blue curve and $h(t-\tau)$ ⇒ green curve
$($this is shifted to the right with the motion parameter $t$ $)$
(J) Plot of $x(\tau) \cdot h(t - \tau)$ ⇒ purple curve, dynamic with $t$
(K) Successive representation of the output signal $y(t)$ ⇒ brown curve
(L) Area for exercise execution: Exercise selection.
(M) Exercise execution: Area for exercise description
(N) Exercise execution: Area for the sample solution
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2006 by Markus Elsberger as part of his bachelor thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- Last revision and English version 2020/2021 by Carolin Mirschina in the context of a working student activity.
The conversion of this applet to HTML 5 was financially supported by Studienzuschüsse ("study grants") of the TUM Faculty EI. Many thanks.