Difference between revisions of "Aufgaben:Exercise 5.1: Sampling Theorem"
From LNTwww
m (Text replacement - "Time Discrete" to "Discrete-Time") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
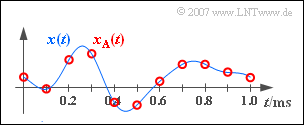
| − | [[File:P_ID1126__Sig_A_5_1.png|right|frame| | + | [[File:P_ID1126__Sig_A_5_1.png|right|frame|Sampling of an analog signal $x(t)$]] |
| − | Given is an | + | Given is an analog signal $x(t)$ according to the sketch: |
| − | *It is known that this signal does not contain any frequencies higher than $B_{\rm NF} = 4 \ \text{kHz}$ | + | *It is known that this signal does not contain any frequencies higher than $B_{\rm NF} = 4 \ \text{kHz}$. |
*By sampling with the sampling rate $f_{\rm A}$ , the signal $x_{\rm A}(t)$ sketched in red in the diagram is obtained. | *By sampling with the sampling rate $f_{\rm A}$ , the signal $x_{\rm A}(t)$ sketched in red in the diagram is obtained. | ||
*For signal reconstruction a low-pass filter is used, for whose frequency response applies: | *For signal reconstruction a low-pass filter is used, for whose frequency response applies: | ||
| Line 31: | Line 31: | ||
''Hints:'' | ''Hints:'' | ||
| − | *This task belongs to the chapter [[Signal_Representation/Time_Discrete_Signal_Representation|Time | + | *This task belongs to the chapter [[Signal_Representation/Time_Discrete_Signal_Representation|Discrete-Time Signal Representation]]. |
| − | *There is an interactive applet for the topic dealt with here: [[Applets: | + | *There is an interactive applet for the topic dealt with here: [[Applets:Sampling_of_Analog_Signals_and_Signal_Reconstruction|Sampling of Analog Signals and Signal Reconstruction]] |
| Line 54: | Line 54: | ||
$f_{1,\ \text{min}}\ = \ ${ 4 3% } $\text{kHz}$ | $f_{1,\ \text{min}}\ = \ ${ 4 3% } $\text{kHz}$ | ||
| − | {What is the maximum size of the upper corner frequency $f_2$ | + | {What is the maximum size of the upper corner frequency $f_2$ that the signal is perfectly reconstructed? |
|type="{}"} | |type="{}"} | ||
$f_{2,\ \text{max}}\ = \ ${ 6 3% } $\text{kHz}$ | $f_{2,\ \text{max}}\ = \ ${ 6 3% } $\text{kHz}$ | ||
| Line 63: | Line 63: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The distance between two adjacent samples is $T_{\rm A} = 0.1 \ \text{ms}$. Thus, for the sampling rate $f_{\rm A} = 1/ T_{\rm A} \;\underline {= 10 \ \text{kHz}}$is obtained. | + | '''(1)''' The distance between two adjacent samples is $T_{\rm A} = 0.1 \ \text{ms}$. Thus, for the sampling rate $f_{\rm A} = 1/ T_{\rm A} \;\underline {= 10 \ \text{kHz}}$is obtained. |
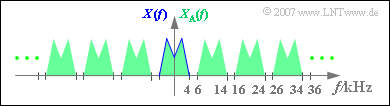
| − | [[File:P_ID1127__Sig_A_5_1_b.png|450px|right|frame|Spectrum $X_{\rm A}(f)$ of the sampled signal (schematic representation)]] | + | [[File:P_ID1127__Sig_A_5_1_b.png|450px|right|frame|Spectrum $X_{\rm A}(f)$ of the sampled signal <br>(schematic representation)]] |
'''(2)''' Proposed <u>solutions 2 and 4</u> are correct: | '''(2)''' Proposed <u>solutions 2 and 4</u> are correct: | ||
*The spectrum $X_{\rm A}(f)$ of the sampled signal is obtained from $X(f)$ by periodic continuation at a distance of $f_{\rm A} = 10 \ \text{kHz}$. | *The spectrum $X_{\rm A}(f)$ of the sampled signal is obtained from $X(f)$ by periodic continuation at a distance of $f_{\rm A} = 10 \ \text{kHz}$. | ||
| − | *From the sketch you can see that $X_{\rm A}(f)$ can have parts at $f = 2.5 \ \text{kHz}$ and $f = 6.5 \ \text{kHz}$ | + | *From the sketch you can see that $X_{\rm A}(f)$ can have signal parts at $f = 2.5 \ \text{kHz}$ and $f = 6.5 \ \text{kHz}$;. |
| − | *In contrast, there are no components at $f = 5.5 \ \text{kHz}$ | + | *In contrast, there are no components at $f = 5.5 \ \text{kHz}$. |
| − | *Also at $f = 34.5 \ \text{kHz}$ will be valid | + | *Also at $f = 34.5 \ \text{kHz}$ will be valid $X_{\rm A}(f) = 0$. |
<br clear=all> | <br clear=all> | ||
| − | '''(3)''' It must be ensured that all frequencies of the | + | '''(3)''' It must be ensured that all frequencies of the analog signal are weighted with $H(f) = 1$. |
*From this follows according to the sketch: | *From this follows according to the sketch: | ||
| Line 80: | Line 80: | ||
'''(4)''' Likewise, it must be guaranteed that all spectral components of $X_{\rm A}(f)$, that are not contained in $X(f)$ are removed by the low-pass filter. | '''(4)''' Likewise, it must be guaranteed that all spectral components of $X_{\rm A}(f)$, that are not contained in $X(f)$ are removed by the low-pass filter. | ||
| − | *According to the sketch, the following must | + | *According to the sketch, the following must apply: |
:$$f_{2, \ \text{max}} = f_{\rm A} – B_{\rm NF} \;\underline{= 6 \ \text{kHz}}.$$ | :$$f_{2, \ \text{max}} = f_{\rm A} – B_{\rm NF} \;\underline{= 6 \ \text{kHz}}.$$ | ||
| Line 86: | Line 86: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^5.1 Discrete-Time Signal Representation^]] |
Latest revision as of 10:03, 11 October 2021
Given is an analog signal $x(t)$ according to the sketch:
- It is known that this signal does not contain any frequencies higher than $B_{\rm NF} = 4 \ \text{kHz}$.
- By sampling with the sampling rate $f_{\rm A}$ , the signal $x_{\rm A}(t)$ sketched in red in the diagram is obtained.
- For signal reconstruction a low-pass filter is used, for whose frequency response applies:
- $$H(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_1 \hspace{0.05cm}, \\ |f| > f_2 \hspace{0.05cm} \\ \end{array}$$
The range between the frequencies $f_1$ and $f_2 > f_1$ is not relevant for the solution of this task.
The corner frequencies $f_1$ and $f_2$ are to be determined in such a way that the output signal $y(t)$ of the low-pass filter exactly matches the signal $x(t)$ .
Hints:
- This task belongs to the chapter Discrete-Time Signal Representation.
- There is an interactive applet for the topic dealt with here: Sampling of Analog Signals and Signal Reconstruction
Questions
Solution
(1) The distance between two adjacent samples is $T_{\rm A} = 0.1 \ \text{ms}$. Thus, for the sampling rate $f_{\rm A} = 1/ T_{\rm A} \;\underline {= 10 \ \text{kHz}}$is obtained.
(2) Proposed solutions 2 and 4 are correct:
- The spectrum $X_{\rm A}(f)$ of the sampled signal is obtained from $X(f)$ by periodic continuation at a distance of $f_{\rm A} = 10 \ \text{kHz}$.
- From the sketch you can see that $X_{\rm A}(f)$ can have signal parts at $f = 2.5 \ \text{kHz}$ and $f = 6.5 \ \text{kHz}$;.
- In contrast, there are no components at $f = 5.5 \ \text{kHz}$.
- Also at $f = 34.5 \ \text{kHz}$ will be valid $X_{\rm A}(f) = 0$.
(3) It must be ensured that all frequencies of the analog signal are weighted with $H(f) = 1$.
- From this follows according to the sketch:
- $$f_{1, \ \text{min}} = B_{\rm NF} \;\underline{= 4 \ \text{kHz}}.$$
(4) Likewise, it must be guaranteed that all spectral components of $X_{\rm A}(f)$, that are not contained in $X(f)$ are removed by the low-pass filter.
- According to the sketch, the following must apply:
- $$f_{2, \ \text{max}} = f_{\rm A} – B_{\rm NF} \;\underline{= 6 \ \text{kHz}}.$$