Difference between revisions of "Aufgaben:Exercise 4.1Z: Appointment to Breakfast"

From LNTwww
m (Text replacement - "Category:Aufgaben zu Stochastische Signaltheorie" to "Category:Theory of Stochastic Signals: Exercises")
 
(9 intermediate revisions by 3 users not shown)
Line 1: Line 1:
  
−
{{quiz-Header|Buchseite=Stochastische Signaltheorie/Zweidimensionale Zufallsgrößen
+
{{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables
 
}}
 
}}
  
−
[[File:P_ID245__Sto_Z_4_1.jpg|right|frame|Kanzlerkandidat(inn)en–Frühstück im Jahr 2002]]
+
[[File:P_ID245__Sto_Z_4_1.jpg|right|frame|Chancellor candidates – breakfast in 2002]]
−
Frau M. und Herr S. treffen sich ja bekanntlich öfter einmal zu einem gemeinsamen Frühstück:  
+
Ms. M. and Mr. S. are known to meet often for a joint breakfast:  
−
*Beide versprechen, an einem bestimmten Tag zwischen 8 Uhr und 9 Uhr zu einem solchen Treffen zu kommen.  
+
*Both promise to come to such a meeting on a certain day between 8 am and 9 am.  
−
*Weiter vereinbaren sie, dass jeder von ihnen in diesem Zeitraum (und nur in diesem) auf „Gut Glück” eintrifft und bis zu einer Viertelstunde auf den Anderen wartet.
+
*Further,&nbsp; they agree that each of them will arrive in this period&nbsp; (and only in this period)&nbsp; on&nbsp; "good luck"&nbsp; <br>and wait up to fifteen minutes for the other.
  
  
Line 12: Line 12:
  
  
 +
Hints:
 +
*The exercise belongs to the chapter&nbsp; [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]].
 +
*Use the minute of arrival time as the time in the following questions:&nbsp; <br>"Minute = 0"&nbsp; stands for 8 o'clock, "Minute = 60"&nbsp; for 9 o'clock.
 +
*The exercise arose before the 2002 German Bundestag elections,&nbsp; when both Dr. Angela Merkel and Dr. Edmund Stoiber wanted to become the CDU/CSU's candidate for chancellor.
 +
*At a joint breakfast in Wolfratshausen,&nbsp; Ms. Merkel renounced.&nbsp; The later election was won by Gerhard Schröder&nbsp; (SPD).
  
  
  
−
''Hinweise:''
+
===Questions===
−
*Die Aufgabe gehört zum  Kapitel&nbsp; [[Theory_of_Stochastic_Signals/Zweidimensionale_Zufallsgrößen|Zweidimensionale Zufallsgrößen]].
 
−
 
−
*Verwenden Sie bei den folgenden Fragen als Zeitangabe die Minute der Ankunftszeit:&nbsp; <br>&bdquo;Minute = 0&rdquo; steht f&uuml;r 8 Uhr,&nbsp; &bdquo;Minute = 60&rdquo; f&uuml;r 9 Uhr.
 
−
*Die Aufgabe entstand vor der Bundestagswahl 2002, als sowohl Dr. Angela Merkel als auch Dr. Edmund Stoiber Kanzlerkandidat(in) der CDU/CSU werden wollten.
 
−
*Bei einem gemeinsamen Frühstück in Wolfratshausen verzichtete Frau Merkel.&nbsp; Die spätere Wahl gewann Gerhard Schröder (SPD).
 
−
 
 
−
 
 
−
 
 
−
 
 
−
===Fragebogen===
 
  
 
<quiz display=simple>
 
<quiz display=simple>
−
{Wie gro&szlig; ist die Wahrscheinlichkeit&nbsp; $p_1$, dass sich die beiden treffen, wenn Herr S. um 8 Uhr 30 ankommt? Begr&uuml;nden Sie Ihre Antwort.
+
{What is the probability&nbsp; $p_1$&nbsp; that the two will meet when Mr. S. arrives at 8:30?&nbsp; Give reasons for your answer.
 
|type="{}"}
 
|type="{}"}
 
$p_1 \ = \ $ { 50 1% } $\ \%$
 
$p_1 \ = \ $ { 50 1% } $\ \%$
  
  
−
{Welche Ankunftszeit sollte Frau M. w&auml;hlen, wenn sie Herrn S. eigentlich nicht treffen m&ouml;chte, sich aber trotzdem an die getroffene Vereinbarung halten will? <br>Wie gro&szlig; ist dann die Wahrscheinlichkeit&nbsp; $p_2$, dass sich Frau M. und Herr S. treffen werden?
+
{Which arrival time should Ms. M. choose if she does not actually want to meet Mr. S.,&nbsp; but still wants to keep to the agreement made? <br>What is the probability&nbsp; $p_2$&nbsp; that Ms. M. and Mr. S. will meet?
 
|type="{}"}
 
|type="{}"}
−
$p_2 \ = \ $ { 25 1% } $\ \%$
+
$p_2 \ = \ $ { 25 1% } $\ \%$
  
  
−
{Welche Ankunftszeit sollte Frau M. w&auml;hlen, wenn sie nicht nur ein Treffen m&ouml;glichst vermeiden, sondern die Wartezeit minimieren m&ouml;chte?
+
{Which arrival time should Ms. M. choose if she not only wants to avoid a meeting as much as possible,&nbsp; but also wants to minimize the waiting time?
 
|type="{}"}
 
|type="{}"}
−
$\rm Minute \ = \ ${ 60 }
+
$\rm minute \ = \ ${ 60 }
  
  
−
{Wie gro&szlig; ist die Wahrscheinlichkeit&nbsp; $p_4$&nbsp; f&uuml;r ein Zusammentreffen generell, das heißt, wenn beide tats&auml;chlich auf &bdquo;Gut Gl&uuml;ck&rdquo; erscheinen?
+
{What is the probability&nbsp; $p_4$&nbsp; for a meeting in general,&nbsp; that is,&nbsp; if both actually appear on "good luck"?
 
|type="{}"}
 
|type="{}"}
−
$p_4 \ = \ $ { 43.75 1% } $\ \%$
+
$p_4 \ = \ $ { 43.75 1% } $\ \%$
  
  
Line 51: Line 46:
 
</quiz>
 
</quiz>
  
−
===Musterlösung===
+
===Solution===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
−
'''(1)'''&nbsp; Kommt Herr S. um 8 Uhr 30, so trifft er Frau M., wenn diese zwischen 8 Uhr 15 und 8 Uhr 45 ankommt. Damit ist die Wahrscheinlichkeit
+
'''(1)'''&nbsp; If Mr. S. arrives at 8:30,&nbsp; he will meet Ms. M. if she arrives between 8:15 and 8:45.&nbsp; Thus the probability:
−
:$$p_1 = \text{Pr(Herr S. trifft Frau M.)}\hspace{0.15cm}\underline{=50\%}.$$
+
:$$p_1 = \text{Pr(Mr. S. meets Ms. M.)}\hspace{0.15cm}\underline{=50\%}.$$
  
  
−
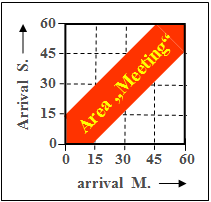
[[File:EN_Sto_Z_4_1_d.png|right|frame|&bdquo;Günstiger Bereich&rdquo; für Zusammentreffen]]
+
[[File:EN_Sto_Z_4_1_d_neu.png|right|frame|"Favorable area"&nbsp; for meeting]]
−
'''(2)'''&nbsp; Kommt Frau M. um 8 Uhr, so trifft sie Herrn S. nur dann, wenn dieser vor 8 Uhr 15 kommt.  
+
'''(2)'''&nbsp; If Ms. M. arrives at 8 a.m.,&nbsp; she meets Mr. S. only if he arrives before 8:15.  
−
*Erscheint Frau M. um 9 Uhr, dann muss Herr S. nach 8 Uhr 45 angekommen sein, damit sich beide treffen k&ouml;nnen.  
+
*If Ms. M. arrives at 9 a.m.,&nbsp; Mr. S. must arrive after 8:45 a.m. so that they can meet.  
−
*Die Wahrscheinlichkeit f&uuml;r ein Zusammentreffen ist in beiden F&auml;llen:  
+
*The probability of meeting is the same in both cases:  
−
:$$p_2 = \big[\text{Min Pr(Herr S. trifft Frau M.)}\big]\hspace{0.15cm}\underline{=25\%}.$$
+
:$$p_2 = \big[\text{Min Pr(Mr. S. meets Ms. M.)}\big]\hspace{0.15cm}\underline{=25\%}.$$
  
  
−
'''(3)'''&nbsp; Von den beiden unter&nbsp;&nbsp; '''(2)''' berechneten Ankunftszeiten ist 9 Uhr&nbsp; $(\underline{\text{Minute = 60}})$&nbsp; g&uuml;nstiger, <br>&nbsp; &nbsp; &nbsp; &nbsp; da sie &ndash; falls Herr S. nicht da ist &ndash; sofort wieder gehen kann.
+
'''(3)'''&nbsp; Of the two arrival times calculated in&nbsp; '''(2)''',&nbsp; 9 o'clock&nbsp; $(\underline{\text{Minute = 60}})$&nbsp; is more favorable, <br>&nbsp; &nbsp; &nbsp; since she &ndash; if Mr. S. is not there &ndash; can leave immediately.
  
  
  
−
'''(4)'''&nbsp; Die Wahrscheinlichkeit&nbsp; $p_4$&nbsp; ergibt sich als das Verh&auml;ltnis der roten Fl&auml;che in der Grafik zur Gesamtfl&auml;che&nbsp; $1$.  
+
'''(4)'''&nbsp; The probability&nbsp; $p_4$&nbsp; is given as the ratio of the red area in the graph to the total area&nbsp; $1$.  
−
*Mit den Dreiecksfl&auml;chen erh&auml;lt man:
+
*Using the triangular areas,&nbsp; one obtains:
 
:$$p_4=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 43.75\%}.$$
 
:$$p_4=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 43.75\%}.$$
  
Line 76: Line 71:
  
  
−
[[Category:Theory of Stochastic Signals: Exercises|^4.1 Zweidimensionale Zufallsgrößen^]]
+
[[Category:Theory of Stochastic Signals: Exercises|^4.1 Two-Dimensional Random Variables^]]

Latest revision as of 16:56, 22 February 2022

Chancellor candidates – breakfast in 2002

Ms. M. and Mr. S. are known to meet often for a joint breakfast:

  • Both promise to come to such a meeting on a certain day between 8 am and 9 am.
  • Further,  they agree that each of them will arrive in this period  (and only in this period)  on  "good luck" 
    and wait up to fifteen minutes for the other.



Hints:

  • The exercise belongs to the chapter  Two-Dimensional Random Variables.
  • Use the minute of arrival time as the time in the following questions: 
    "Minute = 0"  stands for 8 o'clock, "Minute = 60"  for 9 o'clock.
  • The exercise arose before the 2002 German Bundestag elections,  when both Dr. Angela Merkel and Dr. Edmund Stoiber wanted to become the CDU/CSU's candidate for chancellor.
  • At a joint breakfast in Wolfratshausen,  Ms. Merkel renounced.  The later election was won by Gerhard Schröder  (SPD).


Questions

1

What is the probability  $p_1$  that the two will meet when Mr. S. arrives at 8:30?  Give reasons for your answer.

$p_1 \ = \ $

$\ \%$

2

Which arrival time should Ms. M. choose if she does not actually want to meet Mr. S.,  but still wants to keep to the agreement made?
What is the probability  $p_2$  that Ms. M. and Mr. S. will meet?

$p_2 \ = \ $

$\ \%$

3

Which arrival time should Ms. M. choose if she not only wants to avoid a meeting as much as possible,  but also wants to minimize the waiting time?

$\rm minute \ = \ $

4

What is the probability  $p_4$  for a meeting in general,  that is,  if both actually appear on "good luck"?

$p_4 \ = \ $

$\ \%$


Solution

Solution

(1)  If Mr. S. arrives at 8:30,  he will meet Ms. M. if she arrives between 8:15 and 8:45.  Thus the probability:

$$p_1 = \text{Pr(Mr. S. meets Ms. M.)}\hspace{0.15cm}\underline{=50\%}.$$


"Favorable area"  for meeting

(2)  If Ms. M. arrives at 8 a.m.,  she meets Mr. S. only if he arrives before 8:15.

  • If Ms. M. arrives at 9 a.m.,  Mr. S. must arrive after 8:45 a.m. so that they can meet.
  • The probability of meeting is the same in both cases:
$$p_2 = \big[\text{Min Pr(Mr. S. meets Ms. M.)}\big]\hspace{0.15cm}\underline{=25\%}.$$


(3)  Of the two arrival times calculated in  (2),  9 o'clock  $(\underline{\text{Minute = 60}})$  is more favorable,
      since she – if Mr. S. is not there – can leave immediately.


(4)  The probability  $p_4$  is given as the ratio of the red area in the graph to the total area  $1$.

  • Using the triangular areas,  one obtains:
$$p_4=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 43.75\%}.$$

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_4.1Z:_Appointment_to_Breakfast&oldid=45564"
  • Powered by MediaWiki