Difference between revisions of "Aufgaben:Exercise 3.7: Angular Modulation of a Harmonic Oscillation"
m (Text replacement - "Category:Aufgaben zu Modulationsverfahren" to "Category:Modulation Methods: Exercises") |
m (→Solution) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Frequency_Modulation_(FM) |
}} | }} | ||
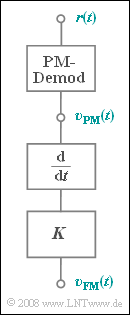
| − | [[File:P_ID1103__Mod_Z_3_6.png|right|frame|Demodulator <br> | + | [[File:P_ID1103__Mod_Z_3_6.png|right|frame|Demodulator <br>for FM]] |
| − | + | The signal arriving at a receiver is: | |
:$$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$ | :$$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$ | ||
| − | + | $r(t)$ is an angle-modulated signal that was neither distorted nor influenced by noise during transmission. | |
| − | + | The signals $v_{\rm PM}(t)$ and $v_{\rm FM}(t)$ result after ideal demodulation by means of | |
| − | * | + | * a phase demodulator, given by the equation |
:$$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$ | :$$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$ | ||
| − | * | + | * a frequency demodulator, consisting of a PM demodulator, a differentiator and a constant $K$. |
| − | + | In order for all signals to have equal units, this constant $K$ is dimensionally constrained. | |
| Line 23: | Line 23: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Frequency_Modulation_(FM)|Frequency Modulation]]. |
| − | * | + | *Reference is also made to the chapter [[Modulation_Methods/Phase_Modulation_(PM)|Phase Modulation]] and particularly to the section [[Modulation_Methods/Frequency_Modulation_(FM)#Signal_characteristics_with_frequency_modulation|Signal characteristics with frequency modulation]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are definitely true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + There could be a PM modulation. |
| − | + | + | + There could be a FM modulation. |
| − | - | + | - The message phase is definitely $ϕ_{\rm N} = 0$. |
| − | + | + | + The message phase is definitely $f_{\rm N} = 10 \ \rm kHz$. |
| − | { | + | {Calculate the signal $v_{\rm PM}(t)$ after the phase demodulator. What is the signal value at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
$v_{\rm PM}(t = 0) \ = \ $ { 1.5 3% } $\ \rm V$ | $v_{\rm PM}(t = 0) \ = \ $ { 1.5 3% } $\ \rm V$ | ||
| − | { | + | {Calculate the signal $v_{\rm FM}(t)$. What is the message phase $ϕ_{\rm N}$? |
|type="{}"} | |type="{}"} | ||
$ϕ_{\rm N} \ = \ $ { 90 3% } $\ \rm Grad$ | $ϕ_{\rm N} \ = \ $ { 90 3% } $\ \rm Grad$ | ||
| − | { | + | {How should $K$ be chosen so that the amplitude of $v_{\rm FM}(t)$ is equal to $1.5 \ \rm V$ ? |
|type="{}"} | |type="{}"} | ||
$K\ = \ $ { 6.28 3% } $\ \rm \cdot 10^4 \ 1/s$ | $K\ = \ $ { 6.28 3% } $\ \rm \cdot 10^4 \ 1/s$ | ||
| − | { | + | {Which of the following statements is true for the FM-modulated signal? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The phase deviation is $ϕ_{\rm max} = 3$. |
| − | + | + | + The frequency deviation is $Δf_{\rm A} = 30 \ \rm kHz$. |
| − | + | + | + The instantaneous frequencies are between $0.97\ \rm MHz$ and $1.03 \ \rm MHz$ . |
| − | - | + | - If $f_{\rm N} = 5 \ \rm kHz$ , the phase deviation would be unchanged. |
| − | + | + | + If $f_{\rm N} = 5 \ \rm kHz$ the frequency deviation would be unchanged. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Answers 1, 2 and 4</u> are correct: |
| − | * | + | *From the equation for $r(t)$ it can only be ascertained that it is an angle modulation, |
| − | * | + | *but not whether it is a phase modulation (PM) or a frequency modulation (FM). |
| − | * | + | *Based on the equation, it is clear that the message frequency is $f_{\rm N} = 10 \ \rm kHz$ . |
| − | * | + | *The phase $ϕ_{\rm N} = 0$ of the source signal would then only apply, if phase modulation were present. |
| − | '''(2)''' | + | '''(2)''' With the modulator constant $K_{\rm PM} = 2 \ \rm V^{–1}$ this is given by: |
:$$v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) = \frac{3}{2\,{\rm V}^{-1}} \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | :$$v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) = \frac{3}{2\,{\rm V}^{-1}} \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$ | ||
| − | * | + | *At time $t = 0$ it therefore holds that: |
:$$v_{\rm PM}(t = 0) = {A_{\rm N}} \hspace{0.15cm}\underline {= 1.5\,{\rm V}}\hspace{0.05cm}.$$ | :$$v_{\rm PM}(t = 0) = {A_{\rm N}} \hspace{0.15cm}\underline {= 1.5\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The output signal $v_{\rm FM}(t)$ of the FM demodulator – consisting of a PM–demodulator and differentiator – can be written as: |
:$$v_{\rm FM}(t) = \frac{{\rm d}v_{\rm PM}(t)}{{\rm d}t} \cdot K = \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot (- \sin(2 \pi \cdot {f_{\rm N}} \cdot t))= \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot \cos(2 \pi \cdot {f_{\rm N}} \cdot t + 90^\circ)\hspace{0.05cm}.$$ | :$$v_{\rm FM}(t) = \frac{{\rm d}v_{\rm PM}(t)}{{\rm d}t} \cdot K = \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot (- \sin(2 \pi \cdot {f_{\rm N}} \cdot t))= \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot \cos(2 \pi \cdot {f_{\rm N}} \cdot t + 90^\circ)\hspace{0.05cm}.$$ | ||
| − | * | + | *The message phase is thus $ϕ_{\rm N} \hspace{0.15cm}\underline {= 90^\circ}$. |
| − | '''(4)''' In | + | '''(4)''' In this case, it must hold that: |
:$$ K ={2 \pi \cdot f_{\rm N}} \hspace{0.15cm}\underline { = 6.28 \cdot 10^{4} \,\,{1}/{ s}} \hspace{0.05cm}.$$ | :$$ K ={2 \pi \cdot f_{\rm N}} \hspace{0.15cm}\underline { = 6.28 \cdot 10^{4} \,\,{1}/{ s}} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' <u>Answers 1, 2, 3 and 5</u> are correct: |
| − | * | + | *The phase deviation is identical to the modulation index, which can be discerned from the equation given: |
:$$\phi_{\rm max} = \eta = 3 = \frac{\Delta f_{\rm A}}{ f_{\rm N}} \hspace{0.05cm}.$$ | :$$\phi_{\rm max} = \eta = 3 = \frac{\Delta f_{\rm A}}{ f_{\rm N}} \hspace{0.05cm}.$$ | ||
| − | * | + | *This leads to the frequency deviation $Δf_{\rm A} = 3 · f_{\rm N} = 30 \ \rm kHz$. |
| − | * | + | *With a carrier frequency of $f_{\rm T} = 1 \ \rm MHz$ , the instantaneous frequency $f_{\rm T}(t)$ can only take values between $1±0.03 \ \rm MHz$ . |
| − | ''' | + | '''Thus, the following statement is also valid:''': |
| − | + | At half the message frequency, the phase deviation $η$ doubles, while the frequency deviation $Δf_{\rm A}$ is unaffected: | |
:$$\eta = \frac{K_{\rm PM} \cdot A_{\rm N}}{ f_{\rm N}} = 6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} = \eta \cdot f_{\rm N} = 6 \cdot 5\,{\rm kHz} = 30\,{\rm kHz}\hspace{0.05cm}.$$ | :$$\eta = \frac{K_{\rm PM} \cdot A_{\rm N}}{ f_{\rm N}} = 6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} = \eta \cdot f_{\rm N} = 6 \cdot 5\,{\rm kHz} = 30\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| Line 107: | Line 107: | ||
| − | [[Category:Modulation Methods: Exercises|^3.2 | + | [[Category:Modulation Methods: Exercises|^3.2 Frequency Modulation^]] |
Latest revision as of 16:14, 9 April 2022
The signal arriving at a receiver is:
- $$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$
$r(t)$ is an angle-modulated signal that was neither distorted nor influenced by noise during transmission.
The signals $v_{\rm PM}(t)$ and $v_{\rm FM}(t)$ result after ideal demodulation by means of
- a phase demodulator, given by the equation
- $$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$
- a frequency demodulator, consisting of a PM demodulator, a differentiator and a constant $K$.
In order for all signals to have equal units, this constant $K$ is dimensionally constrained.
Hints:
- This exercise belongs to the chapter Frequency Modulation.
- Reference is also made to the chapter Phase Modulation and particularly to the section Signal characteristics with frequency modulation.
Questions
Solution
- From the equation for $r(t)$ it can only be ascertained that it is an angle modulation,
- but not whether it is a phase modulation (PM) or a frequency modulation (FM).
- Based on the equation, it is clear that the message frequency is $f_{\rm N} = 10 \ \rm kHz$ .
- The phase $ϕ_{\rm N} = 0$ of the source signal would then only apply, if phase modulation were present.
(2) With the modulator constant $K_{\rm PM} = 2 \ \rm V^{–1}$ this is given by:
- $$v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) = \frac{3}{2\,{\rm V}^{-1}} \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
- At time $t = 0$ it therefore holds that:
- $$v_{\rm PM}(t = 0) = {A_{\rm N}} \hspace{0.15cm}\underline {= 1.5\,{\rm V}}\hspace{0.05cm}.$$
(3) The output signal $v_{\rm FM}(t)$ of the FM demodulator – consisting of a PM–demodulator and differentiator – can be written as:
- $$v_{\rm FM}(t) = \frac{{\rm d}v_{\rm PM}(t)}{{\rm d}t} \cdot K = \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot (- \sin(2 \pi \cdot {f_{\rm N}} \cdot t))= \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot \cos(2 \pi \cdot {f_{\rm N}} \cdot t + 90^\circ)\hspace{0.05cm}.$$
- The message phase is thus $ϕ_{\rm N} \hspace{0.15cm}\underline {= 90^\circ}$.
(4) In this case, it must hold that:
- $$ K ={2 \pi \cdot f_{\rm N}} \hspace{0.15cm}\underline { = 6.28 \cdot 10^{4} \,\,{1}/{ s}} \hspace{0.05cm}.$$
(5) Answers 1, 2, 3 and 5 are correct:
- The phase deviation is identical to the modulation index, which can be discerned from the equation given:
- $$\phi_{\rm max} = \eta = 3 = \frac{\Delta f_{\rm A}}{ f_{\rm N}} \hspace{0.05cm}.$$
- This leads to the frequency deviation $Δf_{\rm A} = 3 · f_{\rm N} = 30 \ \rm kHz$.
- With a carrier frequency of $f_{\rm T} = 1 \ \rm MHz$ , the instantaneous frequency $f_{\rm T}(t)$ can only take values between $1±0.03 \ \rm MHz$ .
Thus, the following statement is also valid::
At half the message frequency, the phase deviation $η$ doubles, while the frequency deviation $Δf_{\rm A}$ is unaffected:
- $$\eta = \frac{K_{\rm PM} \cdot A_{\rm N}}{ f_{\rm N}} = 6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} = \eta \cdot f_{\rm N} = 6 \cdot 5\,{\rm kHz} = 30\,{\rm kHz}\hspace{0.05cm}.$$