Difference between revisions of "Aufgaben:Exercise 2.5: Half-Wave Rectification"
| (3 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
[[File:P_ID311__Sig_A_2_5.png|right|frame|Rectified cosine functions]] | [[File:P_ID311__Sig_A_2_5.png|right|frame|Rectified cosine functions]] | ||
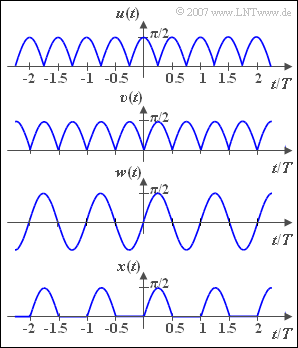
| − | We are looking for the Fourier coefficients of the signal $x(t)$, sketched below, which results from the one-way rectification of the sinusoidal signal $w(t)$ with amplitude $\pi /2$ | + | We are looking for the Fourier coefficients of the signal $x(t)$, sketched below, which results from the one-way rectification of the sinusoidal signal $w(t)$ with amplitude $\pi /2$. |
| − | The Fourier series representation of the signal $u(t)$ sketched above is assumed to be known. This was already determined in [[Aufgaben:Aufgabe_2.4:_Gleichgerichteter_Cosinus| | + | The Fourier series representation of the signal $u(t)$ sketched above is assumed to be known. This was already determined in [[Aufgaben:Aufgabe_2.4:_Gleichgerichteter_Cosinus|Exercise 2.4]]. Taking into account the amplitude $\pi /2$ the following applies: |
:$$u(t)=1+\frac{2}{3} \cdot \cos(\omega_1t)-\frac{2}{15}\cdot \cos(2\omega_1t)+\frac{2}{35}\cdot \cos(3\omega_1t)-\dots$$ | :$$u(t)=1+\frac{2}{3} \cdot \cos(\omega_1t)-\frac{2}{15}\cdot \cos(2\omega_1t)+\frac{2}{35}\cdot \cos(3\omega_1t)-\dots$$ | ||
It should be noted: | It should be noted: | ||
| − | *The | + | *The basic circular frequency is denoted by $\omega_1$ . But since the period of the signals $u(t)$ and $v(t)$ is $T/2$, $\omega_1 = 2\pi /(T/2) = 4 \pi /T$. |
| − | *Because in this task the signals $u(t)$, $w(t)$ and $x(t)$ are to be related to each other, the signal $u(t)$ must also be represented with the period duration $T$ of the signal $x(t)$ | + | *Because in this task the signals $u(t)$, $w(t)$ and $x(t)$ are to be related to each other, the signal $u(t)$ must also be represented with the period duration $T$ of the signal $x(t)$. |
*With $\omega_0 = 2\pi /T = \omega_1/2$ the same applies: | *With $\omega_0 = 2\pi /T = \omega_1/2$ the same applies: | ||
| Line 37: | Line 37: | ||
''Hints:'' | ''Hints:'' | ||
| − | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Series| | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Series|Fourier Series]]. |
*You can find a compact summary of the topic in the two learning videos | *You can find a compact summary of the topic in the two learning videos | ||
| − | ::[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]], | + | ::[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] ⇒ "To calculate the Fourier coefficients", |
| − | ::[[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]]. | + | :: [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] ⇒ "Properties of the Fourier series representation". |
| Line 47: | Line 47: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Calculate the Fourier coefficients of the signal $v(t)$. What is | + | {Calculate the Fourier coefficients of the signal $v(t)$. What is the coefficient $A_2$? |
|type="{}"} | |type="{}"} | ||
$v(t)$: $A_2\ = \ $ { -0.67--0.66 } | $v(t)$: $A_2\ = \ $ { -0.67--0.66 } | ||
| − | {Calculate the Fourier coefficients of the signal $w(t)$. What is | + | {Calculate the Fourier coefficients of the signal $w(t)$. What is the coefficient $B_1$? |
|type="{}"} | |type="{}"} | ||
$w(t)$: $B_1\ = \ $ { 1.571 3% } | $w(t)$: $B_1\ = \ $ { 1.571 3% } | ||
| − | {How can $x(t)$ be composed of $v(t)$ and $w(t)$ | + | {How can $x(t)$ be composed of $v(t)$ and $w(t)$? Give the corresponding Fourier coefficients of the signal $x(t)$. In particular: |
|type="{}"} | |type="{}"} | ||
$x(t)$: $A_0\ = \ $ { 0.5 3% } | $x(t)$: $A_0\ = \ $ { 0.5 3% } | ||
| Line 66: | Line 66: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' The shifted signal $v(t)$ is also even and all sine coefficients are accordingly zero. | '''(1)''' The shifted signal $v(t)$ is also even and all sine coefficients are accordingly zero. | ||
| − | *Nothing changes in the DC signal coefficient | + | *Nothing changes in the DC signal coefficient: $A_0 = 1$. |
*From the signal curves it can be seen that $v(t) = u(t - T/4)$ applies: | *From the signal curves it can be seen that $v(t) = u(t - T/4)$ applies: | ||
| Line 90: | Line 90: | ||
| − | '''(2)''' | + | '''(2)''' Because of $w(t) = \pi /2 \cdot \sin(\omega_0 t)$ all Fourier coefficients except $B_1 = \pi /2 \hspace{0.1cm}\underline{=1.571}$ are zero. |
Latest revision as of 14:14, 15 April 2021
We are looking for the Fourier coefficients of the signal $x(t)$, sketched below, which results from the one-way rectification of the sinusoidal signal $w(t)$ with amplitude $\pi /2$.
The Fourier series representation of the signal $u(t)$ sketched above is assumed to be known. This was already determined in Exercise 2.4. Taking into account the amplitude $\pi /2$ the following applies:
- $$u(t)=1+\frac{2}{3} \cdot \cos(\omega_1t)-\frac{2}{15}\cdot \cos(2\omega_1t)+\frac{2}{35}\cdot \cos(3\omega_1t)-\dots$$
It should be noted:
- The basic circular frequency is denoted by $\omega_1$ . But since the period of the signals $u(t)$ and $v(t)$ is $T/2$, $\omega_1 = 2\pi /(T/2) = 4 \pi /T$.
- Because in this task the signals $u(t)$, $w(t)$ and $x(t)$ are to be related to each other, the signal $u(t)$ must also be represented with the period duration $T$ of the signal $x(t)$.
- With $\omega_0 = 2\pi /T = \omega_1/2$ the same applies:
- $$u(t)=1+\frac{2}{3} \cdot \cos(2\omega_0t)-\frac{2}{15} \cdot \cos(4\omega_0t)+\frac{2}{35} \cdot \cos(6\omega_0t)-\dots$$
For the Fourier coefficients this means:
- The DC coefficient results in $A_0 = 1$,
- All sine coefficients are $B_n = 0$,
- The cosine coefficients with odd $n = 1, \ 3, \ 5, \dots$ are all $0$,
- The cosine coefficients with even $n = 2, \ 4, \ 6, \dots$ are not equal to $0$ :
- $$A_n=(-1)^{\hspace{0.01cm}n/2+1}\frac{2}{n^2-1}.$$
This results in the following numerical values:
- $$A_1=A_3=A_5=\dots=0,$$
- $$A_2=2/3; \;A_4=-2/15;\;A_6=2/35;\;A_8=-2/63.$$
Hints:
- This exercise belongs to the chapter Fourier Series.
- You can find a compact summary of the topic in the two learning videos
- Zur Berechnung der Fourierkoeffizienten ⇒ "To calculate the Fourier coefficients",
- Eigenschaften der Fourierreihendarstellung ⇒ "Properties of the Fourier series representation".
Questions
Solution
- Nothing changes in the DC signal coefficient: $A_0 = 1$.
- From the signal curves it can be seen that $v(t) = u(t - T/4)$ applies:
- $$v(t)=1+\frac{2}{3}\cdot \cos(2\omega_0(t-\frac{T}{4}))-\frac{2}{15}\cdot \cos(4\omega_0(t-\frac{T}{4}))+\frac{2}{35}\cdot \cos(6\omega_0(t-\frac{T}{4}))-\dots$$
- The cosine terms can now be transformed with $\omega_0 \cdot T = 2 \pi$ :
- $$\cos(2\omega_0(t-\frac{T}{4}))=\cos(2\omega_0t-\pi)=-\cos(2\omega_0t),$$
- $$\cos(4\omega_0(t-\frac{T}{4}))=\cos(4\omega_0t-2\pi)=\cos(4\omega_0t),$$
- $$\cos(6\omega_0(t-\frac{T}{4}))=\cos(6\omega_0t-3\pi)=-\cos(6\omega_0t).$$
- This gives us for the Fourier series:
- $$v(t)=1-{2}/{3}\cdot \cos(2\omega_0t)-{2}/{15}\cdot \cos(4\omega_0t)-{2}/{35}\cdot \cos(6\omega_0t)-\dots$$
- or for the cosine coefficients with even-numbered $n$:
- $$A_n=\frac{-2}{n^2-1}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}A_2=-\hspace{-0.05cm}2/3 \hspace{0.1cm}\underline{= -\hspace{-0.05cm}0.667}.$$
(2) Because of $w(t) = \pi /2 \cdot \sin(\omega_0 t)$ all Fourier coefficients except $B_1 = \pi /2 \hspace{0.1cm}\underline{=1.571}$ are zero.
(3) From the graphical representation one can see the relationship $x(t)={1}/{2} \cdot \big [v(t)+w(t) \big].$ This means:
- $$x(t)=\frac{1}{2}+\frac{\pi}{4}\cdot \sin(\omega_0 t)-\frac{1}{3}\cdot \cos(2\omega_0 t)-\frac{1}{15}\cdot \cos(4\omega_0 t)-\frac{1}{35}\cdot \cos(6\omega_0 t)-\ldots$$
- The Fourier coefficients sought are thus:
- $$A_0 \hspace{0.1cm}\underline{=0.5},\hspace{1cm} B_1 = \pi /4 \hspace{0.1cm}\underline{= 0.785},\hspace{1cm} A_2\hspace{0.1cm}\underline{ = -0.333}.$$