Difference between revisions of "Aufgaben:Exercise 3.6Z: Complex Exponential Function"
From LNTwww
m (Text replacement - "bandpass" to "band-pass") |
|||
| Line 4: | Line 4: | ||
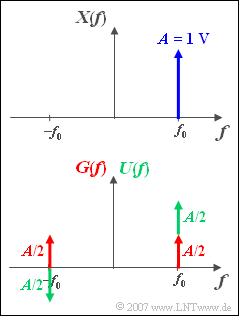
[[File:P_ID518__Sig_Z_3_6_neu.png|right|frame|Splitting the complex exponential function in the spectral domain]] | [[File:P_ID518__Sig_Z_3_6_neu.png|right|frame|Splitting the complex exponential function in the spectral domain]] | ||
| − | In connection with [[Signal_Representation/Differences_and_Similarities_of_LP_and_BP_Signals|" | + | In connection with [[Signal_Representation/Differences_and_Similarities_of_LP_and_BP_Signals|"band-pass systems"]] , one-sided spectra are often used. In the graphic you see such a one-sided spectral function ${X(f)}$, which results in a complex time signal ${x(t)}$. |
In the sketch below, ${X(f)}$ is split into an even component ${G(f)}$ – with respect to the frequency – and an odd component ${U(f)}$. | In the sketch below, ${X(f)}$ is split into an even component ${G(f)}$ – with respect to the frequency – and an odd component ${U(f)}$. | ||
Latest revision as of 16:12, 3 May 2021
In connection with "band-pass systems" , one-sided spectra are often used. In the graphic you see such a one-sided spectral function ${X(f)}$, which results in a complex time signal ${x(t)}$.
In the sketch below, ${X(f)}$ is split into an even component ${G(f)}$ – with respect to the frequency – and an odd component ${U(f)}$.
Hints:
- This exercise belongs to the chapter Fourier Transform Theorems.
- For the first two sub-tasks use the signal parameters $A = 1\, \text{V}$ and $f_0 = 125 \,\text{kHz}$.
- The Shifting Theorem and the Assignment Theorem – are illustrated with examples in the (German language) learning video
Gesetzmäßigkeiten der Fouriertransformation ⇒ "Regularities to the Fourier transform".
Questions
Solution
(1) $G(f)$ is the spectral function of a cosine signal with period $T_0 = 1/f_0 = 8 \, µ\text {s}$:
- $$g( t ) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ).$$
At $t = 1 \, µ\text {s}$ the signal value is equal to $A \cdot \cos(\pi /4)$:
- The real part is $\text{Re}[g(t = 1 \, µ \text {s})] = \;\underline{0.707\, \text{V}}$,
- The imaginary part is $\text{Im}[g(t = 1 \, µ \text {s})] = \;\underline{0.}$
(2) Starting from the Fourier correspondence
- $$A \cdot {\rm \delta} ( f )\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ A$$
is obtained by applying the shifting theorem twice (in the frequency domain):
- $$U( f ) = {A}/{2} \cdot \delta ( {f - f_0 } ) - {A}/{2} \cdot \delta ( {f + f_0 } )\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ u( t ) = {A}/{2} \cdot \left( {{\rm{e}}^{{\rm{j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0\hspace{0.05cm}\cdot \hspace{0.05cm} t} - {\rm{e}}^{{\rm{ - j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t} } \right).$$
- According to Euler's theorem , this can also be written.
- $$u( t ) = {\rm{j}} \cdot A \cdot \sin ( {2{\rm{\pi }}f_0 t} ).$$
- The real part of this signal is always zero.
- At $t = 1 \, µ\text {s}$ the following applies to the imaginary part: $\text{Im}[g(t = 1 \, µ \text {s})] = \;\underline{0.707\, \text{V}}$.
(3) Because $X(f) = G(f) + U(f)$ also holds:
- $$x(t) = g(t) + u(t) = A \cdot \cos ( {2{\rm{\pi }}f_0 t} ) + {\rm{j}} \cdot A \cdot \sin( {2{\rm{\pi }}f_0 t} ).$$
This result can be summarised by "Euler's theorem" as follows:
- $$x(t) = A \cdot {\rm{e}}^{{\rm{j}}\hspace{0.05cm}\cdot \hspace{0.05cm}2{\rm{\pi }}\hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t} .$$
The given alternatives 1 and 3 are correct:
- The signal rotates in the complex plane in a mathematically positive direction, i.e. counterclockwise.
- For one rotation, the "pointer" needs the period $T_0 = 1/f_0 = 8 \, µ\text {s}$.