Difference between revisions of "Aufgaben:Exercise 3.14: Channel Coding Theorem"
m (Text replacement - "”" to """) |
|||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Application_to_Digital_Signal_Transmission |
}} | }} | ||
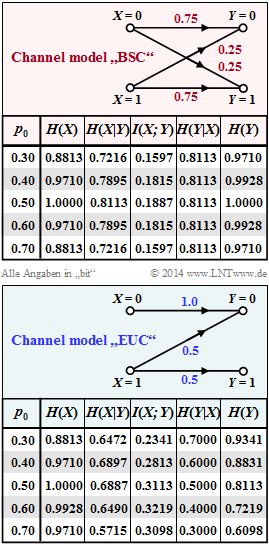
| − | [[File: | + | [[File:EN_Inf_A_3_14.png|right|frame|Information-theoretical quantities of the $\rm BSC$ and $\rm EUC models$]] |
| − | [https:// | + | [https://en.wikipedia.org/wiki/Claude_Shannon Shannon's] channel coding theorem states that an error-free transmission can be made over a "discrete memoryless channel" $\rm(DMC)$ with the code rate $R$ as long as $R$ is not greater than the channel capacity |
:$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | ||
| − | + | The "Channel Coding Theorem" is to be evaluated numerically in this task, whereby two typical channel models are to be considered: | |
| − | * | + | * The $\rm BSC$ model ("Binary Symmetric Channel") with error probability $ε = 0.25$ and channel capacity $C = 1 - H_{\rm bin}(ε),$ |
| − | * | + | * the $\rm EUC$ model (from "Extremely Unsymmetric Channel"; this designation originates from us and is not common) according to [[Aufgaben:Aufgabe_3.11Z:_Extrem_unsymmetrischer_Kanal|Exercise 3.11Z]]. |
| − | + | The graphs show the numerical values of the information-theoretical quantities for the two models $\rm BSC$ and $\rm EUC$: | |
| − | * | + | * The source entropy $H(X),$ |
| − | * | + | * the equivocation $H(X|Y),$ |
| − | * | + | * the mutual information $I(X; Y),$ |
| − | * | + | * the irrelevance $H(Y|X),$ |
| − | * | + | * the sink entropy $H(Y).$ |
| − | + | The parameter in these tables is $p_0 = {\rm Pr}(X = 0)$ in the range between $p_0 = 0.3$ to $p_0 = 0.7$. <br>For the second source symbol probability, $p_1 = {\rm Pr}(X = 1) =1 - p_0$. | |
| Line 27: | Line 27: | ||
| − | + | Hints: | |
| − | + | *The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to Digital Signal Transmission]]. | |
| − | * | + | *Reference is made in particular to the section [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Definition_and_meaning_of_channel_capacity|Definition and meaning of channel capacity]]. |
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true for uncoded transmission ⇒ $\underline{R = 1}$ assuming $p_0 = p_1 = 0.5$ ? |
|type="()"} | |type="()"} | ||
| − | - | + | - BSC results in a smaller bit error probability. |
| − | - | + | - EUC results in a smaller bit error probability. |
| − | + | + | + Both models lead to the same bit error probability. |
| − | { | + | {With $\underline{R = 1}$ the result can be (formally) improved by other values of $p_0$ or $p_1 ? |
|type="()"} | |type="()"} | ||
| − | - | + | - With both channels. |
| − | - | + | - With the BSC model. |
| − | + | + | + With the EUC model. |
| − | - | + | - Not for any model. |
| − | { | + | {Over which channel can error-free transmission be achieved with the $\underline{R = 0.16}$ ? |
|type="()"} | |type="()"} | ||
| − | + | + | + With both channels. |
| − | - | + | - With the BSC model. |
| − | - | + | - With the EUC model. |
| − | - | + | - With none of the models. |
| − | { | + | {Over which channel can error-free transmission be achieved with the $\underline{R = 0.32}$ ? |
|type="()"} | |type="()"} | ||
| − | - | + | - Over both channels. |
| − | - | + | - With the BSC model. |
| − | + | + | + With the EUC model. |
| − | - | + | - With none of the models. |
| − | { | + | {Over which channel can error-free transmission be achieved with the rate $\underline{R = 0.48}$ ? |
|type="()"} | |type="()"} | ||
| − | - | + | - With both channels. |
| − | - | + | - With the BSC model. |
| − | - | + | - With the EUC model. |
| − | + | + | + With none of the models. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Proposed solution 3</u> is correct: |
| − | * | + | *The BSC error probability is with $p_0 = p_1 = 0.5$ for uncoded transmission ⇒ $R = 1$: |
:$$ p_{\rm B} = 0.5 \cdot 0.25 + 0.5 \cdot 0.25=0.25 \hspace{0.05cm}.$$ | :$$ p_{\rm B} = 0.5 \cdot 0.25 + 0.5 \cdot 0.25=0.25 \hspace{0.05cm}.$$ | ||
| − | * | + | *Correspondingly, with the same boundary conditions for the EUC model:: |
:$$ p_{\rm B} = 0.5 \cdot 0 + 0.5 \cdot 0.5=0.25 \hspace{0.05cm}.$$ | :$$ p_{\rm B} = 0.5 \cdot 0 + 0.5 \cdot 0.5=0.25 \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' <u>Proposed solution 3</u> is correct: |
| − | * | + | *In the BSC model with error probability $ε = 0.25$, for uncoded transmission ⇒ $R = 1$ the bit error probability is $p_{\rm B} = 0.25$, regardless of $p_0$ and $p_1$ |
| − | * | + | *In contrast, with the EUC model, for example, a smaller bit error probability is obtained with $p_0 = 0.6$ and $p_1 = 0.4$ : |
:$$p_{\rm B} = 0.6 \cdot 0 + 0.4 \cdot 0.5=0.2 \hspace{0.05cm}.$$ | :$$p_{\rm B} = 0.6 \cdot 0 + 0.4 \cdot 0.5=0.2 \hspace{0.05cm}.$$ | ||
| − | * | + | *Note, however, that now the source entropy is no longer $H(X) = 1\ \rm (bit)$ but only $H(X) = H_{bin} (0.6) = 0.971 \ \rm (bit)$. |
| − | * | + | *In the limiting case $p_0 = 1$, only zeros are transmitted and $H(X) = 0$. For the bit error probability, however, the following then actually applies: |
:$$ p_{\rm B} = 1 \cdot 0 + 0 \cdot 0.5=0 \hspace{0.05cm}.$$ | :$$ p_{\rm B} = 1 \cdot 0 + 0 \cdot 0.5=0 \hspace{0.05cm}.$$ | ||
| − | : | + | :So no information is transmitted, but it is transmitted with the bit error probability "zero". |
| − | '''(3)''' | + | '''(3)''' <u>Proposed solution 1</u> is correct: |
| − | * | + | *From the graph in the information section, it can be read for the capacities of the two channels: |
:$$C_{\rm BSC} = 0.1887 \ \rm {bit/use}, \hspace{0.5cm}C_{rm EUC} = 0.3219 \ \rm {bit/use}.$$ | :$$C_{\rm BSC} = 0.1887 \ \rm {bit/use}, \hspace{0.5cm}C_{rm EUC} = 0.3219 \ \rm {bit/use}.$$ | ||
| − | * | + | *According to the channel coding theorem, a special channel coding can be found at $R ≤ C$ with which the error probability can be made zero. |
| − | * | + | *For both channels this condition is true with rate $R = 0.16$ . |
| − | '''(4)''' | + | '''(4)''' <u>Proposed solution 3</u> is correct: |
| − | * | + | *With the EUC model, the necessary condition $R ≤ C$ for an error-free transmission is fulfilled with $R = 0.32$ and $C = 0.3219$. |
| − | * | + | *However, the prerequisite for this is the probability function $P_X(X) = (0.6,\ 0.4).$ |
| − | * | + | *In contrast, for equally probable symbols ⇒ $P_X(X) = (0.5,\ 0.5)$ the mutual information $I(X; Y) = 0.3113$ would result, <br>i.e. a smaller value than for the channel capacity $C$, and $I(X; Y) < R$ also applies. |
| − | * | + | *It can be seen that the EUC model offers more potential for the application of channel coding than the BSC model. Here, for example, it can be exploited in the code that a transmitted "0" is always transmitted without errors. |
| − | '''(5)''' | + | '''(5)''' The comments on subtasks '''(3)''' and '''(4)''' show that the <u>proposed solution 4</u> applies. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 115: | Line 114: | ||
| − | [[Category:Information Theory: Exercises|^3.3 | + | [[Category:Information Theory: Exercises|^3.3 Application to Digital Signal Transmission^]] |
Latest revision as of 13:50, 17 November 2022
Shannon's channel coding theorem states that an error-free transmission can be made over a "discrete memoryless channel" $\rm(DMC)$ with the code rate $R$ as long as $R$ is not greater than the channel capacity
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
The "Channel Coding Theorem" is to be evaluated numerically in this task, whereby two typical channel models are to be considered:
- The $\rm BSC$ model ("Binary Symmetric Channel") with error probability $ε = 0.25$ and channel capacity $C = 1 - H_{\rm bin}(ε),$
- the $\rm EUC$ model (from "Extremely Unsymmetric Channel"; this designation originates from us and is not common) according to Exercise 3.11Z.
The graphs show the numerical values of the information-theoretical quantities for the two models $\rm BSC$ and $\rm EUC$:
- The source entropy $H(X),$
- the equivocation $H(X|Y),$
- the mutual information $I(X; Y),$
- the irrelevance $H(Y|X),$
- the sink entropy $H(Y).$
The parameter in these tables is $p_0 = {\rm Pr}(X = 0)$ in the range between $p_0 = 0.3$ to $p_0 = 0.7$.
For the second source symbol probability, $p_1 = {\rm Pr}(X = 1) =1 - p_0$.
Hints:
- The exercise belongs to the chapter Application to Digital Signal Transmission.
- Reference is made in particular to the section Definition and meaning of channel capacity.
Questions
Solution
- The BSC error probability is with $p_0 = p_1 = 0.5$ for uncoded transmission ⇒ $R = 1$:
- $$ p_{\rm B} = 0.5 \cdot 0.25 + 0.5 \cdot 0.25=0.25 \hspace{0.05cm}.$$
- Correspondingly, with the same boundary conditions for the EUC model::
- $$ p_{\rm B} = 0.5 \cdot 0 + 0.5 \cdot 0.5=0.25 \hspace{0.05cm}.$$
(2) Proposed solution 3 is correct:
- In the BSC model with error probability $ε = 0.25$, for uncoded transmission ⇒ $R = 1$ the bit error probability is $p_{\rm B} = 0.25$, regardless of $p_0$ and $p_1$
- In contrast, with the EUC model, for example, a smaller bit error probability is obtained with $p_0 = 0.6$ and $p_1 = 0.4$ :
- $$p_{\rm B} = 0.6 \cdot 0 + 0.4 \cdot 0.5=0.2 \hspace{0.05cm}.$$
- Note, however, that now the source entropy is no longer $H(X) = 1\ \rm (bit)$ but only $H(X) = H_{bin} (0.6) = 0.971 \ \rm (bit)$.
- In the limiting case $p_0 = 1$, only zeros are transmitted and $H(X) = 0$. For the bit error probability, however, the following then actually applies:
- $$ p_{\rm B} = 1 \cdot 0 + 0 \cdot 0.5=0 \hspace{0.05cm}.$$
- So no information is transmitted, but it is transmitted with the bit error probability "zero".
(3) Proposed solution 1 is correct:
- From the graph in the information section, it can be read for the capacities of the two channels:
- $$C_{\rm BSC} = 0.1887 \ \rm {bit/use}, \hspace{0.5cm}C_{rm EUC} = 0.3219 \ \rm {bit/use}.$$
- According to the channel coding theorem, a special channel coding can be found at $R ≤ C$ with which the error probability can be made zero.
- For both channels this condition is true with rate $R = 0.16$ .
(4) Proposed solution 3 is correct:
- With the EUC model, the necessary condition $R ≤ C$ for an error-free transmission is fulfilled with $R = 0.32$ and $C = 0.3219$.
- However, the prerequisite for this is the probability function $P_X(X) = (0.6,\ 0.4).$
- In contrast, for equally probable symbols ⇒ $P_X(X) = (0.5,\ 0.5)$ the mutual information $I(X; Y) = 0.3113$ would result,
i.e. a smaller value than for the channel capacity $C$, and $I(X; Y) < R$ also applies. - It can be seen that the EUC model offers more potential for the application of channel coding than the BSC model. Here, for example, it can be exploited in the code that a transmitted "0" is always transmitted without errors.
(5) The comments on subtasks (3) and (4) show that the proposed solution 4 applies.