Difference between revisions of "Aufgaben:Exercise 1.3Z: Exponentially Decreasing Impulse Response"
From LNTwww
| (One intermediate revision by one other user not shown) | |||
| Line 20: | Line 20: | ||
''Please note:'' | ''Please note:'' | ||
| − | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain|System Description in Time Domain]] | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain|System Description in Time Domain]]. |
*The following definite integral is given: | *The following definite integral is given: | ||
:$$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = {\pi}/{2} .$$ | :$$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = {\pi}/{2} .$$ | ||
| Line 57: | Line 57: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' The frequency response $H(f)$ is the Fourier transform of $h(t)$: | '''(1)''' The frequency response $H(f)$ is the Fourier transform of $h(t)$: | ||
| Line 78: | Line 78: | ||
*Using the given definite integral with the result $π/2$ the following is obtained: | *Using the given definite integral with the result $π/2$ the following is obtained: | ||
:$$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$ | :$$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$ | ||
| − | *The result shows that the impulse response at $t = 0$ is equal to the mean value of the left-hand | + | *The result shows that the impulse response at $t = 0$ is equal to the mean value of the left-hand and right-hand limits. |
| − | '''(3)''' The amplitude response in this task or in general with the 3dB- | + | '''(3)''' The amplitude response in this task or in general with the 3dB cut-off frequency $f_{\rm G}$ is: |
:$$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$ | :$$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$ | ||
| − | *By comparing coefficients one obtains: | + | *By comparing the coefficients one obtains: |
:$$f_{\rm G} = \frac{1}{2\pi T} \hspace{0.15cm}\underline{= {\rm 159 \hspace{0.1cm} Hz}}.$$ | :$$f_{\rm G} = \frac{1}{2\pi T} \hspace{0.15cm}\underline{= {\rm 159 \hspace{0.1cm} Hz}}.$$ | ||
| − | '''(4)''' <u>The first | + | '''(4)''' <u>The first statement</u> is correct: |
| − | *Due to $h(t) = 0$ for $t < 0$ | + | *Due to $h(t) = 0$ for $t < 0$: The system is indeed causal. It is a <u>low-pass filter of first order</u>. |
*In contrast, a high-pass filter would have to satisfy the following condition: | *In contrast, a high-pass filter would have to satisfy the following condition: | ||
:$$H(f = 0) = \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm}{\rm d}t = 0.$$ | :$$H(f = 0) = \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm}{\rm d}t = 0.$$ | ||
| − | *$H(f)$ is a complex function. The phase response is (see [[Aufgaben:Exercise_1.1Z:_Low- | + | *$H(f)$ is a complex function. The phase response is (see [[Aufgaben:Exercise_1.1Z:_Low-Pass_Filter_of_1st_and_2nd_Order|Exercise 1.1Z]]): |
:$$b(f) = \arctan {f}/{f_{\rm G}}.$$ | :$$b(f) = \arctan {f}/{f_{\rm G}}.$$ | ||
*For the frequency $f = f_{\rm G}$ one obtains $b(f = f_{\rm G}) = π/4 = 45^\circ$. | *For the frequency $f = f_{\rm G}$ one obtains $b(f = f_{\rm G}) = π/4 = 45^\circ$. | ||
Latest revision as of 18:17, 18 July 2021
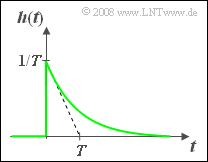
The impulse response $h(t)$ of an LTI system, which
- is identically zero for all times $t < 0$,
- changes abruptly at time $t > 0$, and
- decreases for $t > 0$ according to an exponential function:
- $$h(t) = {1}/{T} \cdot {\rm e}^{-t/T},$$ was measured.
Let the parameter be $T = 1 \hspace{0.15cm} \rm ms$. In the subtask (3) the 3dB cut-off frequency $f_{\rm G}$ is to be determined, which is (implicitly) defined as follows:
- $$|H(f = f_{\rm G})| = {1}/{\sqrt{2}} \cdot|H(f = 0)| .$$
Please note:
- The exercise belongs to the chapter System Description in Time Domain.
- The following definite integral is given:
- $$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = {\pi}/{2} .$$
Questions
Solution
(1) The frequency response $H(f)$ is the Fourier transform of $h(t)$:
- $$H(f) = \int_{-\infty}^{+\infty}h(t) \cdot {\rm e}^{\hspace{0.05cm}{-\rm j}2\pi ft}\hspace{0.15cm} {\rm d}t = \frac{1}{T} \cdot \int_{0}^{+\infty} {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\hspace{0.15cm} {\rm d}t.$$
- Integration leads to the result:
- $$H(f) = \left[ \frac{-1/T}{{\rm j}2\pi f+{1}/{T}} \cdot {\rm e}^{\hspace{0.05cm}{-(\rm j}2\pi f+ {1}/{T}) t}\right]_{0}^{\infty}= \frac{1}{1+{\rm j} \cdot 2\pi fT}.$$
- At frequency $f = 0$ the frequency response has the value $H(f = 0) \; \underline{= 1}$.
(2) This frequency response can also be written with real and imaginary parts as follows:
- $$H(f) = \frac{1}{1+(2\pi fT)^2} -{\rm j} \cdot \frac{2\pi fT}{1+(2\pi fT)^2}.$$
- The impulse response at time $t = 0$ is equal to the integral over $H(f)$.
- Since the imaginary part is odd only the real part has to be integrated over.
- Using the symmetry property one obtains:
- $$h(t=0)=2 \cdot \int_{ 0 }^{ \infty } \frac{1}{1+(2\pi fT)^2} \hspace{0.1cm}{\rm d}f = \frac{1}{\pi T} \cdot \int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x .$$
- Using the given definite integral with the result $π/2$ the following is obtained:
- $$h(t=0)= \frac{1}{2 T} \hspace{0.15cm}\underline{= {\rm 500\cdot 1/s}}.$$
- The result shows that the impulse response at $t = 0$ is equal to the mean value of the left-hand and right-hand limits.
(3) The amplitude response in this task or in general with the 3dB cut-off frequency $f_{\rm G}$ is:
- $$|H(f)| = \frac{1}{\sqrt{1+(2\pi fT)^2}} = \frac{1}{\sqrt{1+(f/f_{\rm G})^2}}.$$
- By comparing the coefficients one obtains:
- $$f_{\rm G} = \frac{1}{2\pi T} \hspace{0.15cm}\underline{= {\rm 159 \hspace{0.1cm} Hz}}.$$
(4) The first statement is correct:
- Due to $h(t) = 0$ for $t < 0$: The system is indeed causal. It is a low-pass filter of first order.
- In contrast, a high-pass filter would have to satisfy the following condition:
- $$H(f = 0) = \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm}{\rm d}t = 0.$$
- $H(f)$ is a complex function. The phase response is (see Exercise 1.1Z):
- $$b(f) = \arctan {f}/{f_{\rm G}}.$$
- For the frequency $f = f_{\rm G}$ one obtains $b(f = f_{\rm G}) = π/4 = 45^\circ$.
- If a cosine signal of frequency $f = f_{\rm G}$ is applied ot the input, the output signal is given by:
- $$y(t) = K \cdot \cos( 2 \pi f_{\rm G} t - 45^{\circ}).$$
- This signal is a harmonic oscillation but not a cosine signal.