Difference between revisions of "Aufgaben:Exercise 3.5Z: Application of the Residue Theorem"
| (12 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
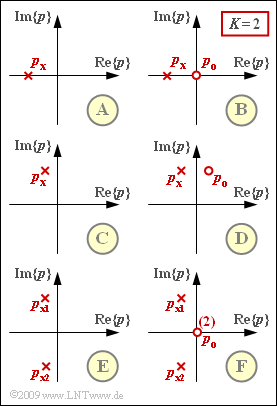
| − | [[File:P_ID1781__LZI_Z_3_5.png|right|frame|Six | + | [[File:P_ID1781__LZI_Z_3_5.png|right|frame|Six pole–zero configurations]] |
Let the spectral function $Y_{\rm L}(p)$ be given in pole–zero notation characterized by | Let the spectral function $Y_{\rm L}(p)$ be given in pole–zero notation characterized by | ||
*$Z$ zeros $p_{{\rm o}i}$, | *$Z$ zeros $p_{{\rm o}i}$, | ||
| Line 10: | Line 10: | ||
| − | In the following, the configurations shown in the diagram are considered. Let always $K= 2$ hold. | + | In the following, the configurations shown in the diagram are considered. Let always $K= 2$ hold. |
| − | In the case that the number $Z$ of zeros is less than the number $N$ of poles, the corresponding time signal $y(t)$ can be determined directly by applying the [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Formulation_of_the_residue_theorem|residue theorem]] . | + | In the case that the number $Z$ of zeros is less than the number $N$ of poles, the corresponding time signal $y(t)$ can be determined directly by applying the [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform#Formulation_of_the_residue_theorem|residue theorem]] . |
| − | In this case | + | In this case: |
:$$y(t) = \sum_{i=1}^{I} \left \{ | :$$y(t) = \sum_{i=1}^{I} \left \{ | ||
Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p | Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p | ||
| Line 20: | Line 20: | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \right | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \right | ||
\} \hspace{0.05cm}.$$ | \} \hspace{0.05cm}.$$ | ||
| − | $I$ | + | $I$ indicates the number of distinguishable poles; $I = N$ holds for all given constellations. |
| Line 27: | Line 27: | ||
| − | + | Please note: | |
| − | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | |
| − | + | *If the time signal $y(t)$ is complex, then $Y_{\rm L}(p)$ cannot be realized as a circuit. However, the application of the residue theorem is still possible. | |
| − | + | *The complex frequency $p$, the zeros $p_{{\rm o}i}$ as well as the poles $p_{{\rm x}i}$ each describe normalized quantities without units in this exercise. | |
| − | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Inverse_Laplace_Transform|Inverse Laplace Transform]]. | + | *Thus, time $t$ is dimensionless, too. |
| − | |||
| − | * | ||
| − | * | ||
| − | * | ||
| Line 41: | Line 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {For which configurations can the residue theorem <u>not be applied directly</u>? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Configuration $\rm A$, |
| − | + | + | + Configuration $\rm B$, |
| − | - | + | - Configuration $\rm C$, |
| − | + | + | + Configuration $\rm D$, |
| − | - | + | - Configuration $\rm E$, |
| − | + | + | + Configuration $\rm F$. |
| − | { | + | {Compute $y(t)$ for configuration $\rm A$ with $K= 2$ and $p_{\rm x} = -1$. What is the numerical value for time $t = 1$? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Re}\{y(t = 1)\} \ = \ $ { 0.736 3% } | $\ {\rm Re}\{y(t = 1)\} \ = \ $ { 0.736 3% } | ||
| Line 57: | Line 53: | ||
| − | { | + | {Compute $y(t)$ for configuration $\rm C$ with $K= 2$ and $p_{\rm x} = -0.2 + {\rm j} \cdot 1.5\pi$. What numerical value is obtained for time $t = 1$? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Re}\{y(t = 1)\} \ = \ $ { 0. } | $\ {\rm Re}\{y(t = 1)\} \ = \ $ { 0. } | ||
| Line 63: | Line 59: | ||
| − | { | + | {What signal value $y(t = 1)$ is obtained for the constellation $\rm E$ with $K= 2$ and two poles at $p_{\rm x} = -0.2 \pm {\rm j} \cdot 1.5\pi$? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Re}\{y(t = 1)\} \ = \ $ { -0.357--0.337 } | $\ {\rm Re}\{y(t = 1)\} \ = \ $ { -0.357--0.337 } | ||
| Line 74: | Line 70: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Suggested solutions 2, 4 and 6</u> are correct: |
| − | * | + | *The prerequisite for the application of the residue theorem is that there are fewer zeros than poles, that is, $Z < N$ must hold. |
| − | * | + | *This condition is not met for the configurations $\rm B$, $\rm D$ and $\rm F$. |
| − | * | + | *First, a partial fraction decomposition must be made here, for example for configuration $\rm B$ with $p_x = -1$: |
:$$Y_{\rm L}(p)= \frac {p} {p +1}= 1-\frac {1} {p +1} | :$$Y_{\rm L}(p)= \frac {p} {p +1}= 1-\frac {1} {p +1} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| Line 83: | Line 79: | ||
| − | '''(2)''' | + | '''(2)''' Considering $Y_{\rm L}(p) = 2/(p+1)$ it follows from the residue theorem with $I=1$: |
:$$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} | :$$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} | ||
\bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= 2 \cdot {\rm | \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= 2 \cdot {\rm | ||
e}^{- \hspace{0.05cm}t}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y(t=1) | e}^{- \hspace{0.05cm}t}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y(t=1) | ||
| − | =\frac{2}{\rm e} \hspace{0.15cm}\underline{ \approx 0.736 \hspace{0.15cm}{\rm ( | + | =\frac{2}{\rm e} \hspace{0.15cm}\underline{ \approx 0.736 \hspace{0.15cm}{\rm (purely\hspace{0.15cm}real)}} |
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | '''(3)''' | + | [[File:P_ID1782__LZI_Z_3_5_c.png|right|frame|Complex signals at a single complex pole]] |
| + | '''(3)''' Using the same procedure as in subtask '''(2)''' the following is obtained: | ||
:$$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}-(0.2 \hspace{0.05cm}+ | :$$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}-(0.2 \hspace{0.05cm}+ | ||
\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}1.5 \pi) \hspace{0.05cm} \cdot \hspace{0.05cm}t} | \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}1.5 \pi) \hspace{0.05cm} \cdot \hspace{0.05cm}t} | ||
| Line 100: | Line 97: | ||
\hspace{0.05cm}t} | \hspace{0.05cm}t} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *Due to the second term, it is a complex signal whose phase rotates in the mathematically positive direction (counterclockwise) . |
| − | * | + | *For time $t=1$, the following holds: |
:$$y(t = 1) = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2} \cdot \big [ | :$$y(t = 1) = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2} \cdot \big [ | ||
\cos(1.5 \pi) + {\rm j} \cdot \sin(1.5 \pi) | \cos(1.5 \pi) + {\rm j} \cdot \sin(1.5 \pi) | ||
| − | \big ]= - {\rm j} \cdot 1.638 | + | \big ]= - {\rm j} \cdot 1.638$$ |
| + | :$$\Rightarrow | ||
\hspace{0.3cm}{\rm Re}\{y(t = 1)\} \hspace{0.15cm}\underline{ = 0},\hspace{0.2cm} {\rm Im}\{y(t = 1)\} \hspace{0.15cm}\underline{=- 1.638} | \hspace{0.3cm}{\rm Re}\{y(t = 1)\} \hspace{0.15cm}\underline{ = 0},\hspace{0.2cm} {\rm Im}\{y(t = 1)\} \hspace{0.15cm}\underline{=- 1.638} | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *The left graph shows the signal for a pole at $p_x = -2 + {\rm j} \cdot 1.5 \pi$. |
| + | *The right graph shows the conjugate complex signal to it can be seen for $p_x = -2 - {\rm j} \cdot 1.5 \pi$. | ||
| − | |||
| − | + | [[File:P_ID1783__LZI_Z_3_5_d.png|right|frame|Signal curve of configuration $\rm E$]] | |
| − | '''(4)''' | + | '''(4)''' Now $I=2$ holds. The residuals of $p_{x1}$ and $p_{x2}$ yield: |
:$$y_1(t) = | :$$y_1(t) = | ||
\frac {K \cdot (p-p_{{\rm x}1})} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot | \frac {K \cdot (p-p_{{\rm x}1})} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot | ||
| Line 126: | Line 124: | ||
-\frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{-p_{{\rm x}1}\hspace{0.05cm}\cdot | -\frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{-p_{{\rm x}1}\hspace{0.05cm}\cdot | ||
\hspace{0.05cm}t}$$ | \hspace{0.05cm}t}$$ | ||
| − | :$$ | + | :$$y(t)= y_1(t)+y_2(t) = |
| − | |||
\frac {2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 | \frac {2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 | ||
\hspace{0.08cm}\cdot | \hspace{0.08cm}\cdot | ||
\hspace{0.05cm}t}}{{\rm j} \cdot 3 \pi} \cdot \big [ \cos(.) + {\rm j} \cdot \sin(.) | \hspace{0.05cm}t}}{{\rm j} \cdot 3 \pi} \cdot \big [ \cos(.) + {\rm j} \cdot \sin(.) | ||
| − | - \cos(.) + {\rm j} \cdot \sin(.)\big ]= | + | - \cos(.) + {\rm j} \cdot \sin(.)\big ]$$ |
| + | :$$\Rightarrow | ||
| + | \hspace{0.3cm}y(t)= | ||
\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | \frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | ||
\hspace{0.08cm}\cdot | \hspace{0.08cm}\cdot | ||
\hspace{0.05cm}t}\cdot \sin(1.5\pi \cdot t)$$ | \hspace{0.05cm}t}\cdot \sin(1.5\pi \cdot t)$$ | ||
| − | |||
:$$\Rightarrow | :$$\Rightarrow | ||
\hspace{0.3cm}y(t=1)= -\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | \hspace{0.3cm}y(t=1)= -\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 | ||
| Line 142: | Line 140: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | The graph shows the (purely real) signal curve $y(t)$ for this configuration. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 11:12, 10 November 2021
Let the spectral function $Y_{\rm L}(p)$ be given in pole–zero notation characterized by
- $Z$ zeros $p_{{\rm o}i}$,
- $N$ poles $p_{{\rm x}i}$, and
- the constant $K$.
In the following, the configurations shown in the diagram are considered. Let always $K= 2$ hold.
In the case that the number $Z$ of zeros is less than the number $N$ of poles, the corresponding time signal $y(t)$ can be determined directly by applying the residue theorem .
In this case:
- $$y(t) = \sum_{i=1}^{I} \left \{ Y_{\rm L}(p)\cdot (p - p_{{\rm x}i})\cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}i}} \right \} \hspace{0.05cm}.$$
$I$ indicates the number of distinguishable poles; $I = N$ holds for all given constellations.
Please note:
- The exercise belongs to the chapter Inverse Laplace Transform.
- If the time signal $y(t)$ is complex, then $Y_{\rm L}(p)$ cannot be realized as a circuit. However, the application of the residue theorem is still possible.
- The complex frequency $p$, the zeros $p_{{\rm o}i}$ as well as the poles $p_{{\rm x}i}$ each describe normalized quantities without units in this exercise.
- Thus, time $t$ is dimensionless, too.
Questions
Solution
- The prerequisite for the application of the residue theorem is that there are fewer zeros than poles, that is, $Z < N$ must hold.
- This condition is not met for the configurations $\rm B$, $\rm D$ and $\rm F$.
- First, a partial fraction decomposition must be made here, for example for configuration $\rm B$ with $p_x = -1$:
- $$Y_{\rm L}(p)= \frac {p} {p +1}= 1-\frac {1} {p +1} \hspace{0.05cm} .$$
(2) Considering $Y_{\rm L}(p) = 2/(p+1)$ it follows from the residue theorem with $I=1$:
- $$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1}= 2 \cdot {\rm e}^{- \hspace{0.05cm}t}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y(t=1) =\frac{2}{\rm e} \hspace{0.15cm}\underline{ \approx 0.736 \hspace{0.15cm}{\rm (purely\hspace{0.15cm}real)}} \hspace{0.05cm} .$$
(3) Using the same procedure as in subtask (2) the following is obtained:
- $$y(t) = 2 \cdot {\rm e}^{\hspace{0.05cm}-(0.2 \hspace{0.05cm}+ \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}1.5 \pi) \hspace{0.05cm} \cdot \hspace{0.05cm}t} = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t}\cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.08cm}\cdot \hspace{0.05cm}1.5 \pi\hspace{0.05cm}\cdot \hspace{0.05cm}t} \hspace{0.05cm} .$$
- Due to the second term, it is a complex signal whose phase rotates in the mathematically positive direction (counterclockwise) .
- For time $t=1$, the following holds:
- $$y(t = 1) = 2 \cdot {\rm e}^{\hspace{0.05cm}-0.2} \cdot \big [ \cos(1.5 \pi) + {\rm j} \cdot \sin(1.5 \pi) \big ]= - {\rm j} \cdot 1.638$$
- $$\Rightarrow \hspace{0.3cm}{\rm Re}\{y(t = 1)\} \hspace{0.15cm}\underline{ = 0},\hspace{0.2cm} {\rm Im}\{y(t = 1)\} \hspace{0.15cm}\underline{=- 1.638} \hspace{0.05cm} .$$
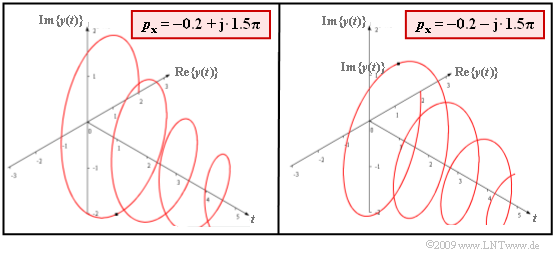
- The left graph shows the signal for a pole at $p_x = -2 + {\rm j} \cdot 1.5 \pi$.
- The right graph shows the conjugate complex signal to it can be seen for $p_x = -2 - {\rm j} \cdot 1.5 \pi$.
(4) Now $I=2$ holds. The residuals of $p_{x1}$ and $p_{x2}$ yield:
- $$y_1(t) = \frac {K \cdot (p-p_{{\rm x}1})} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= \frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}1}\hspace{0.05cm}\cdot \hspace{0.05cm}t} \hspace{0.05cm} ,$$
- $$ y_2(t) = \frac {K } { p_{{\rm x}2}-p_{{\rm x}1}} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}2}\hspace{0.05cm}\cdot \hspace{0.05cm}t}= -\frac {K } { p_{{\rm x}1}-p_{{\rm x}2}} \cdot {\rm e}^{-p_{{\rm x}1}\hspace{0.05cm}\cdot \hspace{0.05cm}t}$$
- $$y(t)= y_1(t)+y_2(t) = \frac {2 \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t}}{{\rm j} \cdot 3 \pi} \cdot \big [ \cos(.) + {\rm j} \cdot \sin(.) - \cos(.) + {\rm j} \cdot \sin(.)\big ]$$
- $$\Rightarrow \hspace{0.3cm}y(t)= \frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t}\cdot \sin(1.5\pi \cdot t)$$
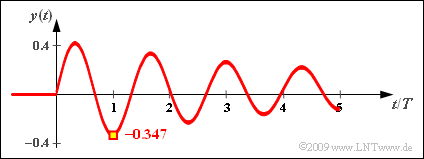
- $$\Rightarrow \hspace{0.3cm}y(t=1)= -\frac {4 }{ 3 \pi} \cdot {\rm e}^{\hspace{0.05cm}-0.2 \hspace{0.08cm}\cdot \hspace{0.05cm}t} \hspace{0.15cm}\underline{= -0.347} \hspace{0.05cm} .$$
The graph shows the (purely real) signal curve $y(t)$ for this configuration.