Difference between revisions of "Aufgaben:Exercise 1.2: Decimal/Binary Converter"
From LNTwww
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Set_Theory_Basics}} |
| − | + | ||
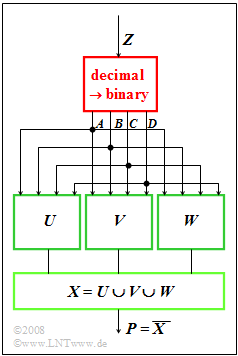
| − | [[File:EN_Sto_A_1_2.png|right|frame| | + | [[File:EN_Sto_A_1_2.png|right|frame|Logical circuit for D/B converting]] |
A number generator $Z$ supplies decimal values in the range $1$ to $15$. | A number generator $Z$ supplies decimal values in the range $1$ to $15$. | ||
*These are converted into binary numbers (block outlined in red). | *These are converted into binary numbers (block outlined in red). | ||
| Line 8: | Line 8: | ||
*For example $Z = 11$ delivers the binary values | *For example $Z = 11$ delivers the binary values | ||
:$$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$ | :$$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$ | ||
| − | Set theoretically, this can be represented as follows: | + | Set-theoretically, this can be represented as follows: |
:$$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D.$$ | :$$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D.$$ | ||
| Line 16: | Line 16: | ||
:$$W,\; {\rm where} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$ | :$$W,\; {\rm where} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$ | ||
*Note that $Z = 0 \ ⇒ \ A = B = C = D = 0$ is already excluded by the number generator. | *Note that $Z = 0 \ ⇒ \ A = B = C = D = 0$ is already excluded by the number generator. | ||
| − | * | + | *Note also that not all input quantities $A$, $B$, $C$ and $D$ are used to calculate all intermediate quantities $U$, $V$ and $W$, resp. |
| Line 22: | Line 22: | ||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Mengentheoretische_Grundlagen|Set theory basic]]. | ||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video: | ||
| − | + | :[[Mengentheoretische_Begriffe_und_Gesetzmäßigkeiten_(Lernvideo)|"Mengentheoretische Begriffe und Gesetzmäßigkeiten"]] ⇒ "Set-theoretical terms and laws". | |
| − | |||
| − | |||
| − | |||
| − | |||
| Line 35: | Line 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which statements are true regarding the random variable $U$ | + | {Which statements are true regarding the random variable $U$? |
|type="[]"} | |type="[]"} | ||
- $U$ contains two elements. | - $U$ contains two elements. | ||
| Line 42: | Line 41: | ||
+ The largest element of $U$ is $14$. | + The largest element of $U$ is $14$. | ||
| − | {Which statements are true regarding the random variable $V$ | + | {Which statements are true regarding the random variable $V$? |
|type="[]"} | |type="[]"} | ||
+ $V$ contains two elements. | + $V$ contains two elements. | ||
| Line 49: | Line 48: | ||
- The largest element of $V$ is $14$. | - The largest element of $V$ is $14$. | ||
| − | {Which statements are true regarding the random variable $W$ | + | {Which statements are true regarding the random variable $W$? |
|type="[]"} | |type="[]"} | ||
+ $W$ contains two elements. | + $W$ contains two elements. | ||
| Line 60: | Line 59: | ||
- $P$ contains all powers of two. | - $P$ contains all powers of two. | ||
+ $P$ contains all prime numbers. | + $P$ contains all prime numbers. | ||
| − | - $P$ describes the empty set | + | - $P$ describes the empty set $\phi$. |
- $P$ is identical with the universal set $G = {1,2, \ \text{...} \ , 15}$. | - $P$ is identical with the universal set $G = {1,2, \ \text{...} \ , 15}$. | ||
| Line 73: | Line 72: | ||
| − | ⇒ <u>Proposed solutions 2 and 4</u> are correct. | + | ⇒ <u>Proposed solutions 2 and 4</u> are correct. |
| − | '''(2)''' The event $V$ consists of the two numbers $4$ (binary 0100) and $6$ (binary 0110) | + | '''(2)''' The event $V$ consists of the two numbers $4$ (binary 0100) and $6$ (binary 0110) ⇒ The correct <u>solutions are 1 and 3</u>. |
| − | |||
| − | ⇒ The correct <u>solutions are 1 and 3</u>. | ||
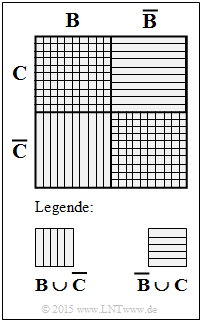
| − | [[File:P_ID2848__Sto_A_1_2c.png|right|frame|Auxiliary Venn | + | [[File:P_ID2848__Sto_A_1_2c.png|right|frame|Auxiliary Venn diagram]] |
| − | '''(3)''' For the event $W$ | + | '''(3)''' For the event $W$, de Morgan's theorem holds: |
:$$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) | :$$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$ | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$ | ||
| − | *Using de Morgan's theorems, it further follows: | + | *Using de Morgan's theorems, it further follows: |
:$$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$ | :$$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$ | ||
| − | *Finally, using the Boolean relation $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ we obtain (see sketch): | + | *Finally, using the Boolean relation $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ we obtain (see sketch): |
:$$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D).$$ | :$$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D).$$ | ||
| − | *Thus, $W$ contains the numbers $15$ and $9$ | + | *Thus, $W$ contains the numbers $15$ and $9$ ⇒ only the <u>proposed solution 1</u> is correct. |
| − | |||
| − | |||
'''(4)''' The union of $U$, $V$ and $W$ contains the following numbers: $4, 6, 8, 9, 10, 12, 14, 15$. | '''(4)''' The union of $U$, $V$ and $W$ contains the following numbers: $4, 6, 8, 9, 10, 12, 14, 15$. | ||
| − | *Accordingly, the set $P$ as the complement of this union is: $P | + | *Accordingly, the set $P$ as the complement of this union is: |
| + | :$$P = {\{1, 2, 3, 5, 7, 11, 13\}}.$$ | ||
*These are exactly the prime numbers which can be represented with four bits ⇒ <u>Proposed solution 2</u>. | *These are exactly the prime numbers which can be represented with four bits ⇒ <u>Proposed solution 2</u>. | ||
Latest revision as of 20:33, 28 November 2021
A number generator $Z$ supplies decimal values in the range $1$ to $15$.
- These are converted into binary numbers (block outlined in red).
- The output consists of the four binary values $A$, $B$, $C$ and $D$ with decreasing significance.
- For example $Z = 11$ delivers the binary values
- $$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$
Set-theoretically, this can be represented as follows:
- $$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D.$$
Three more Boolean expressions are formed from the binary quantities $A$, $B$, $C$ and $D$ and their union set is denoted $X$ :
- \[ U = A \cap \overline{D} \]
- \[ V = \overline{A} \cap B \cap \overline{D} \]
- $$W,\; {\rm where} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$
- Note that $Z = 0 \ ⇒ \ A = B = C = D = 0$ is already excluded by the number generator.
- Note also that not all input quantities $A$, $B$, $C$ and $D$ are used to calculate all intermediate quantities $U$, $V$ and $W$, resp.
Hints:
- The exercise belongs to the chapter Set theory basic.
- The topic of this chapter is illustrated with examples in the (German language) learning video:
- "Mengentheoretische Begriffe und Gesetzmäßigkeiten" ⇒ "Set-theoretical terms and laws".
Questions
Solution
(1) The event $U$ contains
- those numbers greater/equal to eight $(A = 1)$,
- which are even $(D = 0)$: $8, 10, 12, 14$
⇒ Proposed solutions 2 and 4 are correct.
(2) The event $V$ consists of the two numbers $4$ (binary 0100) and $6$ (binary 0110) ⇒ The correct solutions are 1 and 3.
(3) For the event $W$, de Morgan's theorem holds:
- $$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$
- Using de Morgan's theorems, it further follows:
- $$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$
- Finally, using the Boolean relation $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ we obtain (see sketch):
- $$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D).$$
- Thus, $W$ contains the numbers $15$ and $9$ ⇒ only the proposed solution 1 is correct.
(4) The union of $U$, $V$ and $W$ contains the following numbers: $4, 6, 8, 9, 10, 12, 14, 15$.
- Accordingly, the set $P$ as the complement of this union is:
- $$P = {\{1, 2, 3, 5, 7, 11, 13\}}.$$
- These are exactly the prime numbers which can be represented with four bits ⇒ Proposed solution 2.