Difference between revisions of "Aufgaben:Exercise 3.7: Synchronous Demodulator"
| (31 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal Representation/The Convolution Theorem and Operation |
}} | }} | ||
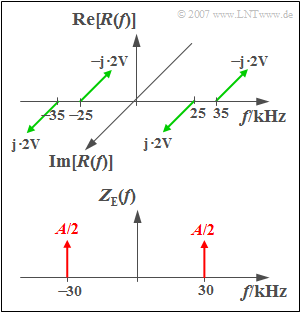
| − | [[File: | + | [[File:Sig_A_3_7_version2.png|right|frame|The spectral functions $R(f)$ and $Z_{\rm E}(f)$]] |
| − | + | To reset an amplitude-modulated signal to the original frequency range, a [[Modulation_Methods/Synchrondemodulation#Blockschaltbild_und_Zeitbereichsdarstellung|"Synchronous Demodulator"]] is often used: | |
| − | + | *This multiplies the AM input signal $r(t)$ with a carrier signal $z_{\rm E}(t)$ on the receiver side, which should match the carrier signal $z_{\rm S}(t)$ on the transmitter side with regard to both frequency $f_{\rm T}$ and phase $\varphi_{\rm T}$. | |
| − | + | *This is followed by a rectangular low-pass filter to eliminate all spectral components above the carrier frequency $f_{\rm T}$. We call the output signal of the synchronous demodulator $v(t)$. | |
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | The spectrum $R(f)$ of the received signal $r(t)$ sketched above is produced by "Two-sideband Amplitude Modulation" of a sinusoidal source signal $q(t)$ with the frequency $5\,\text{kHz}$ and the amplitude $8\,\text{V}$. A cosine signal $z_{\rm S}(t)$ with the frequency $30\,\text{kHz}$ was used as the transmission-side carrier signal. | ||
| + | |||
| + | The spectrum of the carrier signal $z_{\rm E}(t)$ on the receiver side consists of two Dirac deltalines according to the sketch below, each with the weight $A/2$. Since $z_{\rm E}(t)$ is not to contain a unit, the weights of the Dirac functions are also dimensionless. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/The_Convolution_Theorem_and_Operation|The Convolution Theorem and Operation]]. | ||
| + | *Important information can be found on the page [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_of_a_function_with_a_Dirac_function|Convolution of a function with a Dirac function]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Let $f_{\rm T} = 30\,\text{kHz}$ and $A=1$. Calculate the output signal $v(t)$. <br>What signal value occurs at time $t = 50\, {\rm µ} \text{s}$? |
|type="{}"} | |type="{}"} | ||
| − | $v(t=50 \ | + | $v(t = 50\, µ\text{s})\ = \ $ { 4 3% } $\text{V}$ |
| − | { | + | {How large must the amplitude of the carrier signal $z_{\rm E}(t)$ on the receiver side be chosen so that $v(t) = q(t)$ is valid? |
|type="{}"} | |type="{}"} | ||
| − | $A =$ { 2 } | + | $A\ = \ $ { 2 3% } |
| − | { | + | {Calculate the output signal $v(t)$ under the conditions $A = 2$ and $f_{\rm T} = 31\,\text{kHz}$. <br>What signal value occurs at time $ t = 50\, µ\text{s}$? |
|type="{}"} | |type="{}"} | ||
| − | $v(t=50 \ | + | $v(t = 50\, µ\text{s})\ = \ $ { 7.608 3% } $\text{V}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' If we name the signal after the multiplier with $m(t) = r(t) \cdot z_{\rm E}(t)$, the corresponding spectrum $M(f)$ is the convolution product of $R(f)$ and $Z_{\rm E}(f)$. |
| − | + | *Convolution of the spectrum $R(f)$ with the right Dirac delta line at $+30 \text{ kHz}$ leads to discrete spectral lines at $-\hspace{-0.08cm}5\, \text{kHz}$, $+5 \,\text{kHz}$, $+55 \,\text{kHz}$ and $+65 \,\text{kHz}$. These are all imaginary and smaller than the impulse weights of $R(f)$ by a factor of $A/2 = 0.5$. | |
| + | *Convolution of $R(f)$ with the Dirac at $-\hspace{-0.08cm}30 \,\text{kHz}$ yields lines at $-\hspace{-0.08cm}65 \,\text{kHz}$, $-55 \,\text{kHz}$, $-5 \,\text{kHz}$ and $+5 \,\text{kHz}$. | ||
| + | |||
| + | |||
| + | By superimposing the two intermediate results and taking into account the low-pass filter, which suppresses the lines at $\pm 55 \text{ kHz}$ and $\pm 65 \text{ kHz}$ , it thus follows for the spectrum of the sink signal: | ||
| − | $$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm | + | :$$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm with}\hspace{0.3cm}f_{\rm N} = 5\;{\rm kHz}.$$ |
| − | + | *The sink signal $v(t)$ is therefore a $5 \text{ kHz}$–sine signal with amplitude $4 \text{ V}$. | |
| − | + | *The time $t = 50\, µ\text{s}$ corresponds to a quarter of the period $T_0 = 1/f_{\rm N} = 200\, µ\text{s}$. | |
| − | + | *Thus the sink signal is maximum here, i.e. $\underline{4 \text{ V}}$. | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | '''(2)''' With $A = 1$ the sink signal $v(t)$ is only half as large as $q(t)$ ⇒ With $\underline{A = 2}$ both signals would be equal. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The Dirac delta lines at $\pm f_{\rm T}$ each have weight $1$. All spectral lines mentioned below are imaginary and equal in magnitude to $2 \text{ V}$. | ||
| + | *The convolution of $R(f)$ with the right Diracl ine of $z_{\rm E}(t)$ yields components at $-\hspace{-0.08cm}4\, \text{kHz (p: positive)}$, $+6 \,\text{kHz (n: negative)}$, $+56 \,\text{kHz (p)}$ and $+66 \,\text{kHz (n)}$. | ||
| + | *In contrast, the convolution with the left Dirac function leads to spectral lines at $-\hspace{-0.08cm}66 \,\text{kHz (p)}$, $-\hspace{-0.08cm}56 \,\text{kHz (n)}$, $-\hspace{-0.08cm}6 \,\text{kHz (p)}$ und $+4 \,\text{kHz (n)}$, all also with the (magnitude-related) impulse weights $2 \text{ V}$. | ||
| + | *Taking the low–pass into account, there are only the four spectral lines at $\pm 4 \,\text{kHz}$ and $\pm 6 \,\text{kHz}$. | ||
| + | *The associated time signal is thus with $f_4 = 4 \,\text{kHz}$ and $f_6 = 6 \,\text{kHz}$: | ||
| + | :$$v( t ) = 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_4 t} ) + 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_6 t} ) \ne q( t ) = 8\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_5 t} ).$$ | ||
| + | |||
| + | *At time $t = 50\, µ\text{s}$ one obtains: | ||
| + | |||
| + | :$$v( t = 50\, µ\text{s}) = 4\;{\rm{V}} \cdot \big[ {\sin \big ( {0.4{\rm{\pi }}} ) + \sin ( {0.6{\rm{\pi }}} )} \big]\hspace{0.15 cm}\underline{ = 7.608\;{\rm{V}}}{\rm{.}}$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.4 The Convolution Theorem^]] |
Latest revision as of 14:19, 18 January 2023
To reset an amplitude-modulated signal to the original frequency range, a "Synchronous Demodulator" is often used:
- This multiplies the AM input signal $r(t)$ with a carrier signal $z_{\rm E}(t)$ on the receiver side, which should match the carrier signal $z_{\rm S}(t)$ on the transmitter side with regard to both frequency $f_{\rm T}$ and phase $\varphi_{\rm T}$.
- This is followed by a rectangular low-pass filter to eliminate all spectral components above the carrier frequency $f_{\rm T}$. We call the output signal of the synchronous demodulator $v(t)$.
The spectrum $R(f)$ of the received signal $r(t)$ sketched above is produced by "Two-sideband Amplitude Modulation" of a sinusoidal source signal $q(t)$ with the frequency $5\,\text{kHz}$ and the amplitude $8\,\text{V}$. A cosine signal $z_{\rm S}(t)$ with the frequency $30\,\text{kHz}$ was used as the transmission-side carrier signal.
The spectrum of the carrier signal $z_{\rm E}(t)$ on the receiver side consists of two Dirac deltalines according to the sketch below, each with the weight $A/2$. Since $z_{\rm E}(t)$ is not to contain a unit, the weights of the Dirac functions are also dimensionless.
Hints:
- This exercise belongs to the chapter The Convolution Theorem and Operation.
- Important information can be found on the page Convolution of a function with a Dirac function.
Questions
Solution
- Convolution of the spectrum $R(f)$ with the right Dirac delta line at $+30 \text{ kHz}$ leads to discrete spectral lines at $-\hspace{-0.08cm}5\, \text{kHz}$, $+5 \,\text{kHz}$, $+55 \,\text{kHz}$ and $+65 \,\text{kHz}$. These are all imaginary and smaller than the impulse weights of $R(f)$ by a factor of $A/2 = 0.5$.
- Convolution of $R(f)$ with the Dirac at $-\hspace{-0.08cm}30 \,\text{kHz}$ yields lines at $-\hspace{-0.08cm}65 \,\text{kHz}$, $-55 \,\text{kHz}$, $-5 \,\text{kHz}$ and $+5 \,\text{kHz}$.
By superimposing the two intermediate results and taking into account the low-pass filter, which suppresses the lines at $\pm 55 \text{ kHz}$ and $\pm 65 \text{ kHz}$ , it thus follows for the spectrum of the sink signal:
- $$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm with}\hspace{0.3cm}f_{\rm N} = 5\;{\rm kHz}.$$
- The sink signal $v(t)$ is therefore a $5 \text{ kHz}$–sine signal with amplitude $4 \text{ V}$.
- The time $t = 50\, µ\text{s}$ corresponds to a quarter of the period $T_0 = 1/f_{\rm N} = 200\, µ\text{s}$.
- Thus the sink signal is maximum here, i.e. $\underline{4 \text{ V}}$.
(2) With $A = 1$ the sink signal $v(t)$ is only half as large as $q(t)$ ⇒ With $\underline{A = 2}$ both signals would be equal.
(3) The Dirac delta lines at $\pm f_{\rm T}$ each have weight $1$. All spectral lines mentioned below are imaginary and equal in magnitude to $2 \text{ V}$.
- The convolution of $R(f)$ with the right Diracl ine of $z_{\rm E}(t)$ yields components at $-\hspace{-0.08cm}4\, \text{kHz (p: positive)}$, $+6 \,\text{kHz (n: negative)}$, $+56 \,\text{kHz (p)}$ and $+66 \,\text{kHz (n)}$.
- In contrast, the convolution with the left Dirac function leads to spectral lines at $-\hspace{-0.08cm}66 \,\text{kHz (p)}$, $-\hspace{-0.08cm}56 \,\text{kHz (n)}$, $-\hspace{-0.08cm}6 \,\text{kHz (p)}$ und $+4 \,\text{kHz (n)}$, all also with the (magnitude-related) impulse weights $2 \text{ V}$.
- Taking the low–pass into account, there are only the four spectral lines at $\pm 4 \,\text{kHz}$ and $\pm 6 \,\text{kHz}$.
- The associated time signal is thus with $f_4 = 4 \,\text{kHz}$ and $f_6 = 6 \,\text{kHz}$:
- $$v( t ) = 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_4 t} ) + 4\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_6 t} ) \ne q( t ) = 8\;{\rm{V}} \cdot \sin ( {2{\rm{\pi }}f_5 t} ).$$
- At time $t = 50\, µ\text{s}$ one obtains:
- $$v( t = 50\, µ\text{s}) = 4\;{\rm{V}} \cdot \big[ {\sin \big ( {0.4{\rm{\pi }}} ) + \sin ( {0.6{\rm{\pi }}} )} \big]\hspace{0.15 cm}\underline{ = 7.608\;{\rm{V}}}{\rm{.}}$$